
9709
.pdf12
При наглядном моделировании, на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте.
В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.
Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта.
Существенное место при мысленном наглядном моделировании занимает макетирование. Мысленный макет может применяться в случаях, когда протекающие в реальном объекте процессы не поддаются физическому моделированию, либо может предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, однако обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.
Символическое моделирование имеет дело с созданием логических объектов, замещающих реальный, и выражающих изучаемые свойства и отношения определенной системой знаков и символов. Здесь различают знаковое моделирование, где для отдельных понятий и операций между ними вводят условные обозначения, т. е. знаки, и языковое моделирование. В последнем случае каждому понятию и операции соответствует вполне однозначное слово, набор которых образует тезарус (т. е словарь, где каждому слову поставлено в соответствие только одно понятие).
Под математическим моделированием понимают процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.
Для аналитического моделированияхарактерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т. п.) или логических условий. Аналитическая модель может быть исследована следующими методами:
-аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик;
-численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных;
-качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
В случае имитационного моделирования реализующий модель алгоритм воспроизводит функционирование системы во времени. Причем имитируются самые элементарные явления, составляющие изучаемый процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет исследовать достаточно сложные процессы, аналитическое рассмотрение которых затруднено или невозможно.
Комбинированное (аналитико-имитациоиное)моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования.
При реальном моделировании используется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части. Рассмотрим разновидности реального моделирования.
Натурным моделированием называют проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. При
функционировании объекта в соответствии с поставленной целью удается выявить
13
закономерности протекания реального процесса. Надо отметить, что такие разновидности натурного эксперимента, как производственный эксперимент и комплексные испытания, обладают высокой степенью достоверности.
Другим видом реального моделирования являетсяфизическое, отличающееся от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени, а также может рассматриваться без учета времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, которые фиксируются в некоторый момент времени.
С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналогоцифровые (комбинированные).
14
2.3.5 Раздел 2: 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Решение практических задач математическими методами последовательно осуществляется путем математической формулировки задачи (разработки математической модели), выбора метода проведения исследования полученной математической модели, анализа полученного математического результата.
Математическая формулировка задачи обычно представляется в виде чисел, геометрических образов, функций, систем уравнений и т. п.
Теория математического моделирования обеспечивает выявление закономерностей протекания различных явлений окружающего мира или работы систем и устройств путем их математического описания и моделирования без проведения натурных испытаний. При этом используются положения и законы математики, описывающие моделируемые явления, системы или устройства на некотором уровне их идеализации.
Математическая модель (ММ) представляет собой формализованное описание системы (или операции) на некотором абстрактном языке, например, в виде совокупности математических соотношений или схемы алгоритма, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению, получаемому при натурных испытаниях систем или устройств. Любая ММ описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Вид ММ зависит как от природы реального объекта, так и от задач исследования.
Математическое моделирование общественных, экономических, биологических и физических явлений, объектов, систем и различных устройств является одним из важнейших средств познания природы и проектирования самых разнообразных систем и устройств. Известны примеры эффективного использования моделирования в создании ядерных технологий, авиационных и аэрокосмических систем, в прогнозе атмосферных и океанических явлений, погоды и т.д.
Целью математического моделирования является анализ реальных процессов (в природе или технике) математическими методами. В свою очередь, это требует формализации ММ процесса, подлежащего исследованию. Модель может представлять собой математическое выражение, содержащее переменные, поведение которых аналогично поведению реальной системы. Модель может включать элементы случайности, учитывающие вероятности возможных действий двух или большего числа «игроков», как, например, в теории игр; либо она может представлять реальные переменные параметры взаимосвязанных частей действующей системы.
Основные этапы моделирования
1)Постановка задачи. Определение цели анализа и пути ее достижения и выработки общего подходак исследуемой проблеме. На этом этапе требуется глубокое понимание существа поставленной задачи. Иногда, правильно поставить задачу не менее сложно чем ее решить. Постановка - процесс не формальный, общих правил нет.
2)Изучение теоретических основ и сбор информации об объекте оригинала.
На этом этапе подбирается или разрабатывается подходящая теория. Если ее нет, устанавливаются причинно-следственные связи между переменными описывающими объект. Определяются входные и выходные данные, принимаются упрощающие предположения.
3)Формализация. Заключается в выборе системы условных обозначений и с их помощью записывать отношения между составляющими объекта в виде математических выражений. Устанавливается класс задач, к которым может быть отнесена полученная математическая модель объекта. Значения некоторых параметров на этом этапе еще могут быть не конкретизированы.
4)Выбор метода решения. На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта. Для полученной математической задачи выбирается какой-либо метод решения или разрабатывается специальный метод. При выборе метода учитываются знания пользователя, его предпочтения, а также предпочтения разработчика.
5) Построение модели. Выбор типа математической модели. На этом этапе задается некоторый «нематематический» объект — явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
15
6) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.
7) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.
8) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.
9) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.
В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.
Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению. В теории обыкновенных дифференциальных уравнений доказана теорема существования и единственности решения задачи с начальным условием (т. н. задачи Коши). Для уравнений в частных производных получены некоторые теоремы существования и единственности решений для определённых классов начальных и краевых задач.
Дифференциальные уравнения с обыкновенными, а тем более частными производными имеют бесконечное множество решений. Для однозначного определения процесса кроме уравнения необходимо задать еще некоторые дополнительные условия.
Задавая дополнительные условия, нужно помнить, что эти условия должны обеспечивать существование решения (задача не должна быть переопределенной) и единственность решения (задача не должна быть недоопределенной). Желательно также, чтобы выполнялось и условие устойчивости решения (что бывает далеко не всегда).
Рассмотрим основные типы дополнительных условий. 1) Начальные условия.
Определяют состояние системы в некоторый выделенный момент времени, который считается «начальным» (обычно берут t=0). В случае уравнений гиперболического типа, содержащих вторую производную по времени, нужно задать два начальных условия, которые накладываются на функцию решения и ее первую производную по времени. Уравнения параболического типа содержат первую производную по времени, поэтому для него ставится одно начальное условие, накладываемое на решение. Решение уравнения эллиптического типа не зависит от времени, потому для него начальное условие не ставится.
2) Граничные (краевые) условия.
Определяют состояние решения на границе области, в которой ищется решение. Рассмотрим линейные граничные условия. Если, например, изучается процесс колебания струны, то ее концы могут быть закреплены (условие Дирихле), быть свободными (условие Неймана) или быть упруго закрепленными (условие Робена). Граничные условия могут быть более сложными, например, содержать производные по времени. Нелинейные граничные условия оказываются еще более сложными.
Возможны предельные случаи граничных условий. Пусть точка (Mt), в которой ищется решение, расположена «далеко» от границы в том смысле, что возмущение, вышедшее из этой точки, за промежуток времени 0<t<T, в силу конечности скорости распространения возмущения не успевает дойти до границы, то есть в точке (Mt), где 0<t< T, « «граница не чувствуется».
В этом случае приходим к задаче во всем пространстве. Возможен также вариант, когда одни границы «чувствуются», а другие «не чувствуются», в частности, можно получить внешнюю краевую задачу. Во всех этих случаях для обеспечения единственности решения внешних краевых задач необходимо поставить дополнительные условия на бесконечности, что порой является весьма непростым делом. Отметим, что задача в неограниченной области с условиями на бесконечности обычно называется задачей Коши или начальной задачей.
Для стационарных задач существует разделение граничных условий на главные и естественные.
Главные условия обычно имеют вид

16
(2.1)
где  - граница области Ω.
- граница области Ω.
Естественные условия содержат также и производную решения по нормалик границе.
Пример: Уравнение описывает движение тела в поле земного тяготения.
|
(2.2) |
Ему удовлетворяет любая квадратичная функция вида: |
|
y(t)= − gt2 / 2 + at + b |
(2.3) |
где a,b - произвольные числа.
Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.
Задачи математической физики описывают реальные физические процессы, а потому их постановка должна удовлетворять следующим естественным требованиям:
1.Решение должно существовать в каком-либо классе функций;
2.Решение должно быть единственным в каком-либо классе функций;
3.Решение должно непрерывно зависеть от данных (начальных и граничных условий, свободного члена, коэффициентов и т. д.).
Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближенно, и поэтому нужно быть уверенным в том, что решениезадачи в рамках выбранной математической модели не будет существенно зависеть от погрешности измерений.
Математически это требование можно записать, например, так (для независимости от свободного члена):
Пусть задано два дифференциальных уравнения:  с одинаковыми дифференциальными операторами и одинаковыми граничными условия ми, тогда их решения будут непрерывно зависеть от свободного члена, если:
с одинаковыми дифференциальными операторами и одинаковыми граничными условия ми, тогда их решения будут непрерывно зависеть от свободного члена, если:
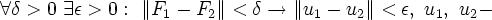 решения соответст вующих уравнений.
решения соответст вующих уравнений.
Множество функций, для которых выполняются перечисленные требования,называется
классом корректности.
Линейные уравнения n-го порядка
Краевая задача для линейного уравнения n-го порядка имеет вид:
(2.4)

17
где - функции |
непрерывны наотрезке |
условия |
заданы линейными формами |
|
|
|
|
(2.5) |
где, |
- заданные числа. |
|
Матрица, составленная из коэффициентов |
имеет ранг m, при этом краевые |
|
условия линейно независимы. Если |
краевая задача называется однородной, |
|
если только |
|
— полуоднородной. |
Системы линейных дифференциальных уравнений
Краевая задача состоит в отыскании системы функций , удовлетворяющей системе линейных дифференциальных уравнений:
(2.6)
и краевым условиям:
где |
- функции, непрерывные на отрезке |
, |
(2.7) |
(2.8)
матрица
имеет ранг |
- заданные числа. |
|
Граничные |
условия в краевых задачах могут задаваться |
различными |
способами. На границе рассматриваемой области можно задать:
1.значение искомой функции;
2.значения производных по пространственным координатам от искомойфункции;
3.уравнение баланса потоков.
Для уравнений теплопроводности чаще задают граничные условия первогои третьего рода. Другими словами, на границе с рассматриваемой областью задаются либо температура Т(х)=Т(с), либо условия теплообмена с внешней средой. При этом если на границе области имеет место конвективный теплообмен,то граничное условие третьего рода записывается в виде:
(2.9)
где α - коэффициент теплообмена, в общем случае являющийся функцией температуры;
 — температура окружающей, среды.
— температура окружающей, среды.

18
Если на границе задан поток |
теплоты, то граничное условие |
(2.10)
где q поток считается положительным, если теплота отводится от рассматриваемого объекта.
Поток q теплоты и конвективный теплообмен не могут задаваться одновременно на одном и том же участке границы. В частном случае, когда граница теплоизолирована, т. е. конвективный теплообмен отсутствует и поток теплоты равен нулю, имеет место граничное условие второго рода:
и
Граничные условия для уравнений Навье-Стокса также могут быть весьма разнообразными. Например, в задаче об обтекании вязкой жидкостью или газом поверхности произвольной формы обычно задаются граничные условия первого рода, причем на границе необходимо задавать значения компонент вектора скорости, плотность и давление.
19
2.3.6 Раздел 2: 2.1 АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Аналитическое моделирование заключается в построении модели, основанной на описании поведения объекта или системы объектов в виде аналитических выражений — формул.
При таком моделировании объект описывается системой линейных или нелинейных алгебраических или дифференциальных уравнений, решение которых может дать представление о свойствах объекта. К полученной аналитической модели, с учетом вида и сложности формул применяются аналитические или приближенные численные методы. Реализация численных методов обычно возлагается на вычислительные машины, обладающие большими вычислительными мощностями. Тем не менее, применение аналитического моделирования ограничено сложностью получения и анализа выражений для больших систем.
Аналитическая модель может быть исследована 3-мя способами:
1.аналитическим способом – стремятся получить в общем виде зависимость от исходных характеристик;
2.численным способом – когда нельзя решить в общем виде, то получаем результаты для конкретных начальных данных;
3.качественным способом – не имея решения управления в общемвиде, мы можем найти некоторые свойства решения; Аналитические модели удобны в использовании, поскольку для аналитического
моделирования не требуются сколько-нибудь значительные затраты вычислительных ресурсов, часто без постановки специальных вычислительных экспериментов исследователь может оценить характер влияния аргументов на выходные параметры, выявить те или иные общие закономерности в поведении системы. Но, к сожалению, аналитическое исследование удается реализовать только для частных случаев сравнительно несложных СМО. Длясложных СМО аналитические модели если и удается получить, то только при принятии упрощающих допущений, ставящих под сомнение адекватность модели.
Исторически первым сложился аналитический подход к исследованию систем. При использовании аналитического подхода ряд свойств одномерной или многомерной, односвязной или многосвязной системы (или какой-либо ее части) отображается в одномерном или n-мерном пространстве одной единственной точкой, совершающей какоелибо движение. Это отображение осуществляется либо с помощью функции f(s), либо посредством оператора (функционала) F(S).
Для любой аналитической модели характерна сложность ее получения. Вместе с тем, после получения она позволяет вычислять полный набор искомых значений выходной величины при полном наборе изменений входной величины.
При использовании данного подхода можно также две или более систем отобразить точками и рассматривать взаимодействие этих точек, каждая из которых совершает какоелибо движение, имеет свое поведение. Поведение точек и их взаимодействие описываются аналитическими законами или закономерностями.
Аналитические методы применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или зависимостей, т.е., когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала. Аналитическое моделирование широко используется при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего (наикратчайшего) пути, оптимальной стратегии поведения в конфликтных ситуациях и т.п.
При практическом применении аналитических представлений для отображения сложных систем следует иметь в виду, что они требуют установки всех детерминированных взаимосвязей между учитываемыми компонентами ицелями системы в виде аналитических
20
зависимостей. Для сложных многокомпонентных, многокритериальных систем получить такие зависимостичрезвычайно сложно, а иногда и невозможно. Более того, если даже это и удается при введении значительных ограничений и допущений, то практически невозможно доказать правомерность применения этих аналитических выражений, т.е. адекватность модели исследуемой системе.
Краевые, начальные и граничные условия для уравнений термогидродинамки вязкой несжимаемой жидкости
Краевые условия задаются до решения задачи. Существуют следующие краевые условия:
а) Геометрические условия: по ним задаются форма, размеры области, для которой разыскивается температурное поле.
б) Физические условия: по ним задаются теплофизические свойства материала области.
в) Начальные условия: они состоят в задании поля температуры в изучаемой области в некоторый начальный момент времени для = ( , , , τ = 0).
Начальные условия задаются только для нестационарных задач.
г) Граничные условия: они состоят в задании особенности сопряжения на границе области, температурного поля в изучаемой области и температурного поля за пределами этой области.
Различают следующие граничные условия:
а) Граничные условия первого рода, тогда в точках границы известны г =
г ( г, г, г, τ)
б) Граничные условия второго рода. По ним задаются в точках границы нормальные составляющие значений плотности теплового потока.
= + = ρ ∙cp T – λ∙gradT
к т
в) Граничные условия третьего рода. По ним не задаётся ни температура в точках границы, ни нормальная составляющая величины плотности теплового потока, а задается связь между ними, то есть физико-математическая зависимость (закон, функция).
qn (xг, yг, zг, ) = α ∙[T(xг, yг, zг, ) – Tж∞] |
(2.11) |
где: α – коэффициент теплоотдачи, Вт/(м2∙оС); Tж∞ - температура задана вдали от границ.
Формулу (2.11) называют законом теплоотдачи Ньютона-Рихмана. Этот закон теплоотдачи был получен опытным путем.
г) Граничные условия четвёртого рода. Они состоят в задании сопряжения (температурного поля в изучаемой области) температуры в точках границы и нормальной составляющей плотности теплового потока.
Температура в точках границы равны ( г, г, г, τ) = ж ( г, г, г, τ).
Так как температуры в точках границы совпадают, поэтому равны и удельные
тепловые потоки: |
|
|
|
|
|
||
|
|
|
|
q (г, г, г, τ) = |
q,ж (г, г, г, τ) |
||
-λ( |
∂ |
)=0 |
= - ж( |
∂ ж |
)=0 |
|
|
|
|
|
|
||||
|
∂ |
|
∂ |
|
|
||
подводится |
отводится |
|
|
||||
теплота |
теплота |
при ж > |
|
||||
В точках на границе жидкость неподвижна. Имеет место наличие ламинарного подслоя, в котором передача теплоты осуществляется теплопроводностью. Толщина пограничного подслоя зависит от среды, которая обтекает стенку.
Сложность решения задач при граничных условиях 4-го рода состоит в том, что нужно одновременно разыскивать поля температур в изучаемой области и за её пределами.
21
Дифференциальные уравнения, описывающие динамику жидкости, определяют решение с точностью до произвольных постоянных. Единственное решение можно выбрать, если задать дополнительно начальныеи граничные условия – это краевые условия. Начальное условие задает искомые поля в момент t = 0, т.е. в момент начала моделирования процесса.
Граничные условия определяют взаимодействие скоростного потока или потока тепла с границами и находящимися в потоке телами. Дифференциальные уравнения в совокупности с краевыми условиями формируют краевую задачу для конкретного гидродинамического процесса.
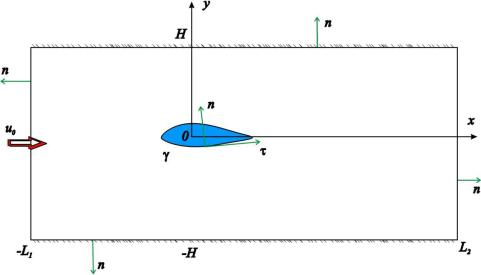
Пример 1. Постановка краевых задач для уравнений Навье – Стокса. Изучение обтекания тела плоским потоком несжимаемой вязкой жидкостив канале.
Рис. 2.1. К постановке задачи об обтекании тела в канале потоком вязкой жидкости
В развернутой форме для компонент вектора скорости = (u,v, w) в декартовой системе координат x, y, z Навье-Стокса для несжимаемой жидкости с постоянной вязкостью имеют вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
= 0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
+ |
|
|
+ |
|
+ |
|
|
= − |
1 |
|
|
|
+ η∆ + , |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
+ |
|
+ |
|
+ |
|
= − |
1 |
|
|
|
|
+ η∆ + , |
|
(2.12) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
+ |
|
+ |
|
+ |
|
= − |
|
1 |
|
|
+ η∆ + |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Слева в уравнениях импульса (2.12) стоят ускорения dvi /dt , а справа – плотности поверхностных сил давления p/x i , вязких сил vi , и массовых сил g i .
