
9481
.pdf
20
Тема 3.
ВЕКТОР СИЛЫ, ОПЕРАЦИИ C СИЛАМИ
3.1. ПРОЕКЦИИ СИЛЫ
Проекцией вектора на ось называется скалярная величина, равная произведению модуля вектора на косинус угла между направлением силы и положительным направлением оси.
То есть проекция вектора на ось L равна
= (, ) = .
Дадим этому определению геометрическое пояснение.
Пусть в трехмерном пространстве задана ось L, направление которой указано вектором единичной длины (направляющим вектором), и вектор, начало которого находится в т. А, а конец, ─ в т. В (рис. 3.1).
Через точки А и В проведем перпендикулярно оси L две плоскости: П1 и П2. Параллельно оси L через точку А проведем направление n.
Численно величина проекции вектора на ось равна отрезку АС или отрезку А1С1, а знак проекции зависит от величины угла:
при 90 проекция силы положительна,
при 90 ─ отрицательна,
при 90 ─ равна нулю.
Можно дать и другое определение проекции вектора на ось.
Проекцией вектора на ось называется скалярное произведение вектора на направляющий вектор оси.
Действительно, = ∙ = (, ) = .,
где ─ угол между направлением вектора и единичного вектора .

21
|
|
B |
|
|
n |
F |
π 2 |
|
|
|
|
α |
С |
L |
А |
|
|
|
|
|
|
С1 |
|
А1 |
|
|
O e
П1 |
П2 |
|
Рис. 3.1
Рассмотрим некоторые частные случаи проецирования вектора на ось:
F |
F |
F |
|
F |
|||
|
|
||
|
|
F |
|
|
|
|
Fx F cos Fx F cos F cos Fx F Fx F Fx 0
Рис. 3.2
Проекцией вектора на плоскость называется вектор, заключенный между проекциями начала и конца вектора на эту плоскость.
Так на рис. 3.3 вектор является проекцией вектора на плокость Oxy. Если вектор задан выражением
|
|
|
|
|
= + + , |
||||
|
|
|
|
|
то аналитическое выражение проекции этого вектора на плоскость Oxy
можно получить, приравняв к нулю проекцию вектора на ось z:
|
|
|
|
|
= + + 0 . |
||
|
|
|
|

22
z
|
|
|
|
C |
|
|
|
|
|
F |
|
|
|
A |
|
|
|
k |
|
|
|
||
|
|
j |
|
B |
y |
|
|
|
|||
|
|
|
|
|
|
i |
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
A2 |
|
F xy |
|
||
|
|
|
|
|
|
B2 |
B1 |
|
|||
|
|
||||
x
Рис. 3.3
Модуль этого вектора равен:
Fxy A1B1 AB AC cos F cos
Для определения проекции силы на ось удобно сначала спроецировать силу на плоскость, в которой эта ось лежит, а затем найденную проекцию спроецировать на ось.
Fx y F cos
Fx Fxy cos F cos cos
Этот прием называют методом двойного проецирования.
Аналогично проецируется сила и на две другие плоскости.
Заметим, что
Проекции вектора на параллельные оси равны.
Проекции вектора на параллельные плоскости геометрически равны.
3.2. СПОСОБЫ ЗАДАНИЯ СИЛЫ
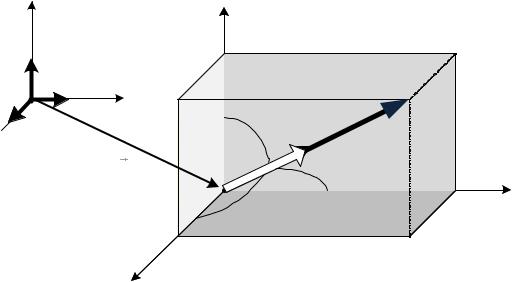
Рассмотрим силу , которая представлена вектором с началом в точке A и с концом в точке B (рис. 3.4).
Для указания точки приложения силы используем радиус-вектор
,= + +
соединяющий начало системы координат и точку приложения силы.
23
Проекции вектора на координатные оси равны координатам точки A , в которой приложена сила .
Информация о величине и направлении силы может быть представлена двумя способами.
z
k O
O
x  i
i
ПЕРВЫЙ СПОСОБ
|
|
z |
|
|
|
|
|
|
Fz |
|
|
|
|
|
y |
Fz |
|
|
|
|
j |
|
|
B |
|||
|
|
|
|
|
||
|
|
|
|
|
e |
|
|
|
|
|
F |
F |
|
|
|
|
|
|
|
F |
|
r |
A |
|
|
|
y |
|
|
A |
|
|
|
Fy |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fy |
|
|
|
|
|
|
|
|
|
Fx |
|
|
|
|
|
x |
|
|
|
|
|
|
|
Рис. 3.4 |
|
|
|
|
Представим вектор силы в виде произведения (рис. 3.4)
= ,
где F − модуль силы, а − единичный вектор, указывающий направление силы (направляющий вектор):
,= + +
где nx , ny , nz − направляющие косинусы вектора (рис. 3.4):
nx |
cos , |
ny cos , |
nz cos . |
Чтобы таким способом задать вектор, необходимо знать углы , , и |
|||
значение его модуля |
F . |
|
|
ВТОРОЙ СПОСОБ (АНАЛИТИЧЕСКИЙ)
Аналитическое выражение вектора силы дается следующим образом:
|
|
|
|
|
= + + , |
||||
|
|
|
|
|

24
где Fx , Fy , Fz − проекции вектора на координатные оси (рис. 3.4).
То есть, для аналитического задания вектора силы необходимо указать три его проекции: Fx , Fy , Fz .
Опишем переход от одного представления к другому.
Допустим, что вектор задан вторым способом, при котором известны три его проекции − Fx , Fy , Fz .
Тогда модуль вектора можно найти как диагональ параллелепипеда:
F
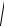 Fx2 Fy2 Fz2 ,
Fx2 Fy2 Fz2 ,
анаправляющие косинусы, для которых выполняется известное соотношение
nx2 ny2 nz2 1,
определить с помощью деления:
nx Fx |
F , ny Fy F , |
nz Fz F. |
В случае, когда например в плоскости вид:
вектор лежит в одной координатной плоскости, Oxy , формулы упростятся и приобретут следующий
F 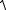
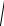 Fx2 Fy2 ,
Fx2 Fy2 ,
nx Fx F, |
ny Fy F , |
причем |
n2 |
n2 |
1. |
|
x |
y |
|
3.3. СЛОЖЕНИЕ СИЛ ГЕОМЕТРИЧЕСКИМ СПОСОБОМ, ТРЕУГОЛЬНИК СИЛ
Существует три способа сложения сил:
1)графический
2)геометрический (графоаналитический)
3)аналитический.
Учитывая, что противоположные стороны параллелограмма равны, сумму двух векторов можно найти, построив вместо параллелограмма сил, треугольник сил (рис. 3.5).
Треугольник сил строится от произвольной точки плоскости путем присоединения начала второго вектора к концу первого вектора.
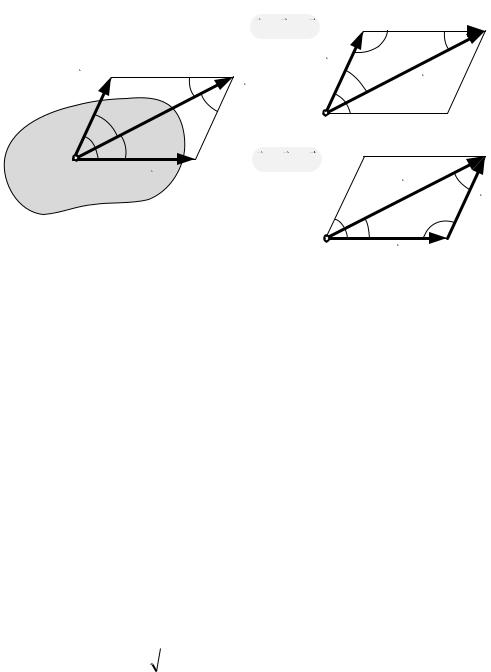
25
Замыкающий вектор геометрически будет равен искомому вектору . Результат суммирования не зависит от порядка следования слагаемых. Следовательно, силовой треугольник может быть построен двумя способами
(рис. 3.5).
|
|
|
F |
|
R F2 |
F1 |
|
1 |
|
|
|
|||
|
|
|
|
|
|
F |
|
|
|
|
|
|
F2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
R F1 F2 |
|
|
|
|
|
|
|
F1 |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
F |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
F1
Рис. 3.5
Суммарный вектор будет являться равнодействующей двух сил, если приложен в точке, где пересекаются линии действия слагаемых сил.
Графический способ сложения сил заключается в построении треугольника сил с помощью карандаша и линейки в заданном масштабе. В настоящее время этот способ практически не применяется.
Геометрический способ решения задач основан на том, что модуль и направление суммы двух сил можно определить, используя формулы тригонометрии для треугольников.
По теореме косинусов для треугольника имеем:
R2 F12 F22 2 F1 F2 cos F12 F22 |
2 F1 F2 cos 180 F12 |
F22 2 F1 F2 cos , |
|||||||||||
откуда модуль равнодействующей |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
|
|
F 2 |
F 2 |
2 F F cos . |
(3.1) |
||||||
|
|
|
|
1 |
|
|
2 |
1 |
2 |
|
|
||
По теореме синусов: |
|
|
|
|
|
|
|
|
|||||
|
R |
|
|
F1 |
|
|
|
F2 |
. |
|
|
(3.2) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
sin |
|
|
sin |
|
sin |
|
|
|
||||
26
Отсюда можно определить направление равнодействующей. Суммирование нескольких сил может выполняться путем
последовательного построения силовых треугольников.
3.4. МНОГОУГОЛЬНИК СИЛ, ГЛАВНЫЙ ВЕКТОР СИСТЕМЫ СИЛ
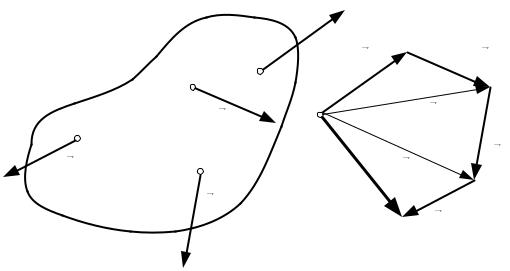
Пусть на твердое тело действует система сил (1, 2, … , ) (рис.3.6).
Вектор, равный векторной (геометрической) сумме всех сил системы, называется главным вектором системы сил:
|
= ∑ |
|
|
(3.3) |
|
=1 |
|
||
|
|
|
|
1.Главный вектор может быть найден для любой системы сил.
2.Главный вектор, как геометрическая сумма всех сил системы, никак не связана с какой-то определенной точкой пространства.
3.Если для некоторой системы сил существует равнодействующая, то она по модулю и направлению совпадает с главным вектором. Неизвестной является только точка ее приложения (линия действия).
Будем обозначать главный вектор , не указывая при этом точку пространства, в которой он был определен.
F1
|
О |
F |
F |
|
1 |
2 |
|
|
О2 |
|
|
|
1 |
|
|
О4 |
F2 |
|
P |
O |
1 |
||
|
|
|
|
|
О |
|
F |
F4 |
|
3 |
|
3 |
|
P2 |
|
|
|
|
|
|
F3 |
R* |
|
|
|
F |
|
|
|
|
|
|
|
|
4 |
Рис.3.6
Графически главный вектор находится с помощью построения многоугольника сил.
27
Выберем произвольную точку О, которую будем называть центром или точкой приведения. Еще раз отметим, что величина и направление главного вектора системы не зависит от положения точки приведения.
Путем последовательного построения треугольника сил будем
суммировать силы |
|
|
|
|
|
, которые геометрически равны заданным |
||||||||
′ |
, ′ |
2 |
, … , ′ |
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
силам |
, |
, … , |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
1 |
+ ′2, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ′3 = ′1 |
+ ′2 |
+ ′3 |
и так далее. |
|||||
|
|
|
2 |
= 1 |
|
|||||||||
В результате получим вектор , представляющий собой геометрическую сумму векторов 1, 2, … , :
= ∑ =1
Полученная в результате построения геометрическая фигура называется силовым многоугольником.
Силовой многоугольник строится путем совмещения начала каждого следующего вектора с концом предыдущего вектора. При этом промежуточные вектора 1, 2… и т.д. показывать не обязательно.
|
|
|
|
|
|
|
|
Векторы ′ |
, ′ |
|
, … , ′ |
|
|
- |
|
2 |
|
называются составляющими, а вектор |
|
||||
1 |
|
|
|
|
|
замыкающим вектором силового многоугольника.
Форма силового многоугольника зависит от порядка суммирования векторов, но сам главный вектор от этого не зависит.
Вслучае плоской системы сил возможно графическое построение многоугольника сил в принятом масштабе сил, на чем основан графический метод решения задач теоретической механики.
Впространственном случае графическое построение многоугольника сил невозможно.
3.5. АНАЛИТИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ
При аналитическом способе суммирования векторов используется известная из векторной алгебры теорема:
Проекция суммы векторов на ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Пусть необходимо найти главный вектор системы сил (1, 2, … , ). Для этого необходимо выполнить сложение n сил:
= ∑ =1

28
Поскольку равны векторы, стоящие в левой и правой частях последнего равенства, должны быть равны и их проекции на ось. Спроецируем это равенство на оси х, у, z:
|
= ∑ |
|
|
= ∑ |
|
|
|
||
|
=1 |
|
=1 |
|
|
||||
|
|
|
|
|
|
|
|||
|
= ∑ |
|
|
= ∑ |
|
|
(3.4) |
||
|
=1 |
|
=1 |
|
|||||
|
|
|
|
|
|
|
|
||
|
= ∑ |
|
|
= ∑ |
|
|
|
||
|
=1 |
|
=1 |
|
|
||||
|
|
|
|
|
|
||||
Далее определим модуль суммарного вектора:
= √( )2 |
+ ( )2 |
+ ( )2 |
(3.5) |
|
|
|
|
и его направляющие косинусы:
|
|
|
|
|
|
|
|
|
|
||
|
= |
|
, |
|
= |
|
, |
|
= |
|
(3.6) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
Итак, мы установили, что проекции главного вектора системы сил на оси координат равны суммам проекций этих сил на соответствующие оси.
Рассмотрим частный случай, когда силовой многоугольник замкнут. В этом случае модуль главного вектора будет равен нулю:
= 0 |
или |
√( )2 |
+ ( )2 |
+ ( )2 |
=0 |
|
|
|
|
|
|
Последнее равенство возможно только если все слагаемые под корнем равны нулю, то есть если
n |
|
|
|
n |
Fix |
0 |
|
X i |
|
i 1 |
|
|
i 1 |
|
n |
|
|
|
n |
Fiy |
0 |
или иначе |
|
Yi |
i 1 |
|
|
|
i 1 |
n |
|
|
|
n |
Fiz |
0 |
|
|
Zi |
i 1 |
|
|
i 1 |
|
0
0 , |
(3.7) |
0
где проекции силы под номером i обозначены Xi , Yi , Zi .
ВЫВОД
Главный вектор системы сил будет равен нулю в том случае, когда все три суммы проекций исходных сил будут равны нулю.

29
3.6. РАСПРЕДЕЛЕННЫЕ СИЛЫ
Понятие о силе, приложенной в точке, является идеализацией реальности. На самом деле взаимодействие тел всегда происходит по некоторой площадке или даже по объему (как у гравитационных сил).
Говоря о сосредоточенной силе, которая приложена в точке, мы на самом деле имеем в виду равнодействующую некоторой силы, распределенной на участке поверхности, размер которого очень мал и в расчёте может не учитываться.
Вмеханике рассматриваются три вида моделей распределенных сил:
1)силы, распределенные вдоль линии;
2)силы, распределенные по поверхности, и
3)силы, распределенные по объему.
Рассмотрим первые два случая.
СИЛЫ, РАСПРЕДЕЛЕННЫЕ ВДОЛЬ ЛИНИИ
Сила, распределенная вдоль линии, характеризуется ее интенсивностью q , которая определяется величиной силы, приходящейся на единицу длины (на 1м) и измеряется в Н/м.
Величина интенсивности может быть переменной q q x (рис. 3.7, а) или постоянной q const (рис. 3.7, б).
q |
а |
q |
б |
|
|
O |
x |
O |
x |
|
|
||
l |
l |
Q ql |
l |
Q q x dx |
|
|
|
|
|
|
|
0 |
|
|
|
Рис. 3.7
В общем случае, когда сила на участке (О, l ) распределена по произвольному закону q q x , ее равнодействующая Q должна быть
вычислена как интеграл. Линия действия равнодействующий Q проходит через центр тяжести подграфика интенсивности, положение которого неизвестно.
Рассмотрим частные случаи.
