
9388
.pdf
Только эта система очень просто «устроена»: сначала нужно решить второе уравнение относительно функции p(x) , а затем вернуться к
первому уравнению и найти y(x) .
К нормальной системе дифференциальных уравнений сводится математическая модель движущейся материальной точки массы m . Пусть
R = + +
r (t) x(t)i y(t) j z(t)k
радиус-вектор этой точки в декартовой системе координат. Скорость и ускорение точки определяются формулами
R
dr
dt
R |
dx R |
|
dy R |
|
dz R |
|||
= v (t) = |
|
i |
+ |
|
j |
+ |
|
k ; |
|
|
|
||||||
|
dt |
|
dt |
|
dt |
|||
R |
|
d 2 x |
d 2r |
R |
|
|
= a(t) = |
|
d t2 |
d t 2 |
R |
+ |
d |
2 |
y |
R |
+ |
d |
2 |
z |
R |
i |
|
j |
|
k . |
||||||
d t 2 |
|
|
|
|||||||
|
|
|
|
d t2 |
||||||
Сила f , под действием которой движется точка, |
является функцией |
|||||||||||||||||||||||||||||||||||||
времени, координат точки и компонент ее скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
R |
R |
|
|
|
|
dx |
|
dy |
|
dz |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
||||||
f |
= f (t, x, y, z, |
, |
, |
) = fxi |
+ f y j |
+ fz k . |
|
|||||||||||||||||||||||||||||||
dt |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 R |
|
f |
|
R |
|
||||
На основании второго закона |
|
Ньютона имеем |
|
|
|
|
r |
|
= |
|
= F |
или в |
||||||||||||||||||||||||||
|
|
|
|
|
d t 2 |
|
m |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
координатной записи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
dx |
|
|
|
dy |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
d |
|
|
= Fx (t, x, y, z, |
, |
|
, |
|
), |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
d t |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||
|
d 2 y |
|
= F (t, x, y, z, |
dx |
|
|
|
dy |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
), |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
d t 2 |
|
|
y |
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
z |
|
|
|
|
|
|
|
dx |
|
|
|
dy |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
d |
|
|
= F (t, x, y, z, |
, |
, |
) |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
d t2 |
|
|
z |
|
|
|
|
|
|
dt |
|
|
dt |
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если считать неизвестными не только координаты точки, но и проекции скорости точки на координатные оси, то придём к нормальной системе из шести дифференциальных уравнений. Здесь производные по переменной t обозначены для краткости точкой сверху.
52

x& = u(t),
y& = v(t),
z& = w(t),
u& = Fx (t, x, y, z,u,v, w),v& = Fy (t, x, y, z,u,v, w),w& = Fz (t, x, y, z,u,v, w)
Решив эту систему, можно получить не только траекторию движения точки, но и закон изменения её скорости.
Покажем, как можно найти интегральные кривые нормальной системы в простейшем случае двух линейных дифференциальных уравнений с постоянными коэффициентами вида
& |
= ax + by |
|
x |
(48.1) |
|
& |
, |
|
y = cx + dy |
|
|
где x = x(t) , y = y(t) – неизвестные функции времени. Из (48.1) следует, что
dy = cx + dy , dx ax + by
а это есть не что иное, как дифференциальное уравнение первого порядка относительно неизвестной функции y = y(x) , правая часть которого
является однородной функцией своих аргументов. Согласно методу решения таких уравнений полагаем y / x = u , где u – новая переменная, и
задача сводится к решению уравнения с разделяющимися переменными u и x .
48.2. Математическая модель «хищник-жертва». К нормальной системе дифференциальных уравнений приводится математическая модель, описывающая борьбу двух видов в живой природе (более подробно см. Ю.И. Неймарк «Математические модели в естествознании и технике», издательство ННГУ, 2004 г.). Эта модель связана с именами биофизика Альфреда Лотки (1880-1949) и математика Вито Вольтерра
(1860-1940).
Рассмотрим пруд, в котором живут караси и щуки. Обозначим через x(t) и y(t) – функции, соответствующие числу карасей и щук в момент
времени t . Будем предполагать, что x и y достаточно велики, чтобы эти
функции можно было считать непрерывными и даже дифференцируемыми. Предполагается также, что в пище для карасей нет
53

недостатка, и в отсутствии щук караси размножаются экспоненциально со скоростью
dx = kx, k > 0, dt
которая пропорциональна их количеству. Что касается щук, то без карасей они вымирают экспоненциально со скоростью
dy = −l y, l > 0. dt
Предположим, что число «встреч» карасей со щуками пропорционально как числу карасей, так и числу щук, поэтому функция, определяющая количество карасей, удовлетворяет уравнению
dx = kx − axy, a > 0. dt
Щуки, съедая карасей, начинают размножаться со скоростью, пропорциональной числу этих «встреч», т.е. в результате получим уравнение
dy = −ly + bxy, b > 0. dt
Таким образом, приходим к системе уравнений Лотки – Вольтерра, представляющей собой простейшую модель экологической системы хищник— жертва
& |
= kx − axy |
|
x |
(48.2) |
|
& |
. |
|
y = −ly + bxy |
|
|
Коэффициенты этой системы «добываются» путём наблюдений, а ее решения находятся с помощью численного интегрирования. Ниже будут показаны графики решений для конкретной системы.
|
Некоторое качественное представление о сосуществовании карасей и |
щук |
может быть получено путем приведения этой системы к |
дифференциальному уравнению, связывающему между собой переменные x и y непосредственно, исключив из рассмотрения переменную t . А
именно, если в системе (48.2) разделить одно уравнение на другое, то приходим к дифференциальному уравнению с разделяющимися переменными
54
k − ay dy = bx − l dx.
y |
x |
(48.3) |
Общее решение этого уравнения |
имеет вид |
k ln y − ay = bx − l ln x + C , |
поэтому его интегральные кривые можно представлять как линии уровня функции
z(x, y) = bx + ay − l ln x − k ln y .
Рис. 48.1
На рис. 48.1 для конкретной системы (48.4) показаны сечения поверхности z(x, y) горизонтальными плоскостями. Из этого рисунка
видно, что ее линии уровня представляют собой замкнутые кривые и что эта функция, по-видимому, имеет минимум. Действительно, приравнивая к нулю частные производные
∂z |
= b − |
l |
|||
|
∂x |
|
|
||
x |
|||||
|
|
||||
|
∂z |
|
k |
||
|
|
|
|
|
|
|
∂y |
= a − y |
|||
|
|
|
|
|
|
получаем, что в точке |
M 0 ( x0 |
= l / b, y0 = k / a) |
возможен экстремум. |
||||||
Вычисляя вторые производные |
|
|
|
|
|
|
|
||
∂2 z = |
l |
, |
|
∂2 z |
= 0, |
∂2 z = |
k |
, |
|
|
|
y2 |
|||||||
∂x2 |
x2 |
|
∂x∂y |
∂y2 |
|
|
|||
убеждаемся, что здесьь выполняется достаточное условие экстремума
55
|
|
AC - B2 = |
l |
× k |
|
> 0 . |
|
|
|
|
|
|
|
|
|
(x0 )2 |
( y0 )2 |
|
|
|
|
|
|
В качестве иллюстрации рассмотрим, например, систему |
|
||||||||||
|
|
& |
= 0,8x − 0,001xy |
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|||
|
|
& |
= − y + 0,001xy |
|
|
|
|
|
|
||
|
|
y |
|
|
|
|
|
(48.4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
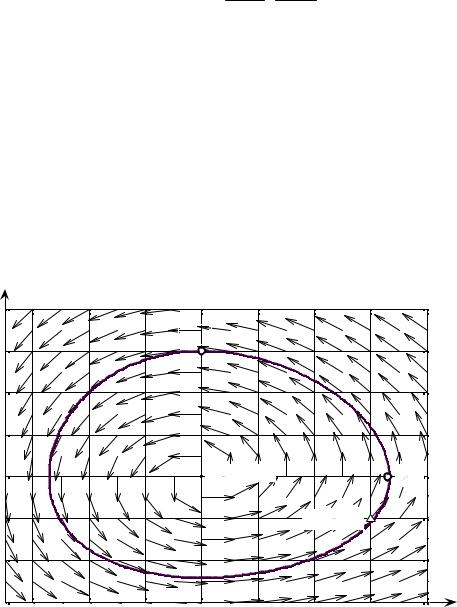
Ее правая часть определяет векторное поле скоростей (см. рис. 48.2) |
|||||||||||
изменения количества карасей и щук: в каждой точке |
( x, y) |
мы имеем |
|||||||||
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
(0,8x − 0,001xy; |
− y + 0,001xy) . |
|
|
|
|||||
1200 |
|
|
|
|
|
|
|
|
|
|
|
1100 |
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
800 |
|
|
(1000,800) |
|
|
|
|
M |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
(1300.700) |
|
|
|
||
600 |
|
|
|
|
|
|
|
|
|
|
|
500 |
800 |
900 |
1000 |
1100 |
1200 |
1300 |
|
1400 |
|
||
700 |
|
|
|||||||||
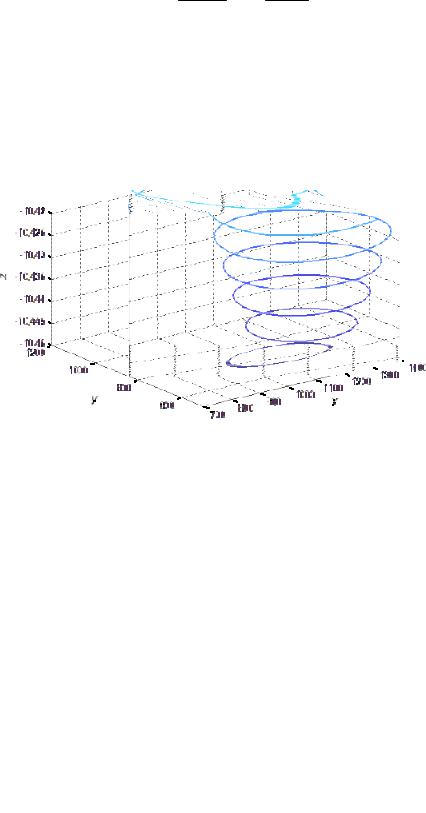
Рис. 48.2
Дифференциальное уравнение (48.3) для этой системы имеет замкнутые интегральные кривые, подобные показанной кривой на рис. 48.2. Решения же x(t) и y(t) системы (48.4) определяют координаты точки,
«пробегаемой» с течением времени по этим интегральным кривым. Каждая замкнутая интегральная кривая соответствует периодическим колебаниям количеств щук и карасей, причем направление «движения» по кривой определяется исходной системой дифференциальных уравнений (48.4).
Пусть, например, сначала было 1300 карасей и 700 щук. Подставляя
эти значения в правую часть системы (48.4), |
получим x(0) = 910 > 0 , |
|
y(0) = 210 > 0 . Следовательно, |
начиная с точки |
& |
(1300,700) происходит |
||
& |
|
|
рост как количества карасей, |
так и количества щук. Затем с точки M1 |
|
|
56 |
|
количество карасей убывает, а количество щук продолжает расти. |
Когда |
|||||||||
пищи для щук станет совсем мало, то их количество начнет уменьшаться (с |
||||||||||
точки M 2 ) и т.д. |
= l / b, y0 = k / a) = (1000, 800) , в |
|
|
|
|
|||||
Точка |
(x0 |
которой |
правые |
части |
||||||
уравнений (48.4) обращаются в ноль, соответствует состоянию равновесия |
||||||||||
системы, когда прирост карасей уравновешивается «деятельностью» |
щук, |
|||||||||
а прирост щук – их естественной смертностью. |
|
|
|
|
||||||
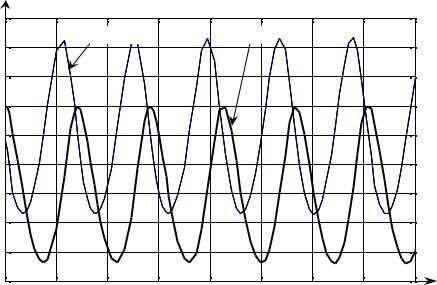
На рис. 48.4 приведены графики решения системы (48.4) с |
|
|||||||||
начальными условиями (x(0) = 1000, y(0) = 1100) , полученные численным |
||||||||||
интегрированием. |
|
|
|
|
|
|
|
|
||
1400 |
|
|
|
|
|
|
|
|
|
|
1300 |
|
|
караси |
|
|
щуки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1200 |
|
|
|
|
|
|
|
|
|
|
1100 |
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
|
|
|
500 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
|
|
|||||||||
Рис.48.4
48.3. Метод исключения. Выше мы показали, как дифференциальное уравнение высокого порядка сводится к нормальной системе дифференциальных уравнений. Иногда систему дифференциальных уравнений решают методом исключения – приведением системы к дифференциальному уравнению высокого порядка. Продемонстрируем этот метод на примере линейной системы второго порядка
|
& |
= ax + by |
x |
||
|
& |
. |
y = cx + dy
Сведём ее решение к решению одного дифференциального уравнения
второго порядка. Для этого продифференцируем по переменной |
t одно из |
|
уравнений системы, например, первое уравнение x = ax + by . |
Для того, |
|
&& & |
& |
|
чтобы исключить из полученного уравнения переменную |
y , подставим в |
|
него y из второго уравнения данной системы |
|
|
& |
|
|
&&x = ax& + bcx + bdy .
57
Наконец, выражая переменную y |
из первого уравнения системы, |
получаем однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно неизвестной функции
x = x(t)
&&x − (a + d )x& − (bс − ad )x = 0 .
Подставив найденное решение |
|
x(t) = C1 x1 (t) + C2 x2 (t) |
в первое уравнение |
|||||
системы, получим вторую функцию |
|
|
||||||
y(t) = |
1 |
& |
1 |
|
& |
& |
(t) − a(C1x1 |
(t) + C2 x2 (t)) . |
|
|
|
||||||
b |
(x − ax) = |
b |
(C1x1 |
(t) + C2 x2 |
||||
|
|
|
|
|
|
|||
Ясно, что метод симметричен. Дифференцируя второе уравнение системы и исключая переменную x , получим уравнение второго порядка относительно функции y = y(t)
&&y − (a + d ) y& − (bс − ad ) y = 0 .
58
Раздел 9. Кратные интегралы
Лекция 49. Двойной интеграл: определение, свойства
В этой лекции мы переходим к рассмотрению способов интегрирования функций многих переменных. Интегралы, которые будут введены, являются обобщением понятия определённого интеграла для функции одной переменной. Напомним, что соответствующая лекция начиналась с рассмотрения задачи вычисления площади криволинейной трапеции. Сохраняя прежнюю логику рассуждений, начнём с геометрической задачи – нахождения объёма цилиндрического тела.
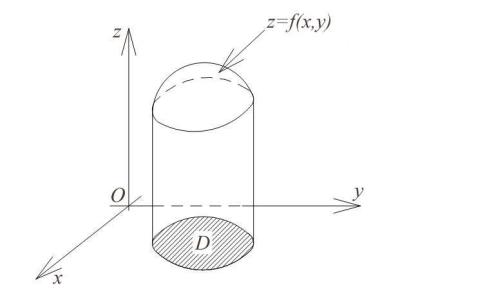
49.1. Задача о вычислении объёма цилиндрического тела. Пусть на плоскости xOу задана область D , ограниченная линией L (где L - замкнутая кривая без самопересечений), и пусть в области D определена некоторая непрерывная функция z = f ( x, y) ³ 0 .
Цилиндрическим телом будем называть тело G , ограниченное
1)плоскостью xOу ,
2)поверхностью z = f ( x, y) ,
3)цилиндрической поверхностью с образующей, параллельной оси Oz и направляющей L (рис. 49.1).
Рис. 49.1
Заметим, что это название достаточно условное. Например, полушар и конус оказываются «цилиндрическими телами». Некоторые авторы употребляют термин «тело с двумя крышками».
59

Ставим задачу найти объём тела G . Отметим, прежде всего, два
принципа, из которых следует исходить при |
определении |
объёма |
произвольного пространственного тела: |
|
|
1. Если тело G разбито на составные части |
G1 , G2 , ..., Gn , |
то его |
объём V равен сумме объёмов всех частей, т.е. V = V1 + V2 +
2. Если цилиндрическое тело G представляет собой прямой цилиндр с высотой H и площадью основания S , то V = SH .
Теперь разобьём область D на подобласти D1, D2 , ..., Dn . Здесь и
далее под разбиением будем понимать представление D в виде объединения областей D1 , D2 , ..., Dn , которые пересекаются между собой
только по границе (т.е. не имеют общих внутренних точек). В соответствии с этим тело G разобьётся на цилиндрические тела G1 , G2 , ..., Gn ,
ограниченные сверху кусками поверхности z = f (x, y) (рис. 49.2).
Рис. 49.2
Выберем в каждой частичной подобласти Di произвольную точку и заменим цилиндрическое тело Gi прямым цилиндром с тем же основанием (площади Si ) и высотой hi = f ( xi , yi ) . По принципу 2
объём этого прямого цилиндра равен V |
i |
= f ( x |
, y |
) |
S |
i |
. Суммируя |
|
i |
i |
|
|
|
объёмы всех прямых цилиндров, получим объём «ступенчатого» тела, дающий приближённое значение объёма исходного цилиндрического тела
n |
|
V ≈ ∑ f (xi , yi ) Si . |
(49.1) |
i=1 |
|
Ясно, что чем «мельче» будет разбита область |
D на части, тем |
60 |
|
точнее объём «ступенчатого» тела будет соответствовать тому числу, которое следует считать объёмом тела G . За точное значение объёма естественно принять предел сумм (49.1) при неограниченном увеличении числа подобластей Di . Переходя к пределу при n → ∞ , потребуем, чтобы
все частичные области стягивались в точку. Для этого введём понятие диаметра области Di как наибольшего расстояния между её точками.
Диаметром разбиения называется наибольший из диаметров областей Di . Обозначим его dn .
Будем считать теперь по определению, что объём тела G есть предел, если он существует, к которому стремится сумма (49.1) при диаметре разбиения, стремящемся к нулю
n |
|
V = lim ∑ f (xi , yi ) Si . |
|
dn →0 i=1 |
|
49.2. Определение двойного |
интеграла. Чтобы ввести |
математическое понятие двойного интеграла функции f ( x, y) по области
D , будем сохранять способ рассуждений, использовавшийся для определения объёма цилиндрического тела.
Рассмотрим в плоскости xOу область D , ограниченную замкнутой
линией L без самопересечений, причём точки, лежащие на границе, будем считать принадлежащими области. Такие области называются
замкнутыми. |
Пусть в |
области D задана функция f ( x, y) . |
Разобьём |
||
область |
на |
|
n частей |
D1, D2 , ..., Dn . В каждой подобласти Di |
выберем |
точку Pi ( xi , yi ) и сформируем так называемую интегральную сумму |
|||||
|
|
|
|
n |
|
|
|
|
|
I n = ∑ f ( xi , yi ) S i , |
|
|
|
|
|
i =1 |
|
где f ( x , y |
) – |
значение функции в точке Pi , а Si – площадь области D . |
|||
i |
i |
|
|
|
i |
Рассмотрим произвольную последовательность интегральных сумм, составленных для функции f ( x, y) в области D при различных
способах разбиения её на части. Будем предполагать, что диаметр разбиения стремится к нулю при n → ∞ .
Если существует предел интегральных сумм In при диаметре разбиения, стремящемся к нулю, и этот предел не зависит ни от способов разбиения области D на подобласти D1, D2 , ..., Dn , ни от выбора точек Pi в каждой подобласти Di , то этот предел называется двойным интегралом функции f ( x, y) по области D и обозначается
∫∫ f ( x, y)ds .
D
Функция f ( x, y) в этом случае называется интегрируемой в областиD ; область D называется областью интегрирования.
61
