Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4629 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Нижегородский Государственный Архитектурно-Строительный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

8779

.pdf
Скачиваний:
0
Добавлен:
25.11.2023
Размер:
1.88 Mб
Скачать
☆

70

равновесия, с помощью которой данная конкретная задача будет решаться наиболее рациональным образом.

8.4. ДРУГИЕ ЧАСТНЫЕ СЛУЧАИ УСЛОВИЙ РАВНОВЕСИЯ

Сходящиеся системы сил

Если линии действия всех сил системы проходят через одну точку, то моменты сил относительно этой точки (или любой проходящей через нее оси) будут равны нулю.

В этом случае уравнения моментов (7.4, г,д,е) оказываются тождествами (т. е. выполняются автоматически); тогда для системы сходящихся сил остаются только уравнения проекций сил:

∑Fix

= 0

 

 

n

 

 

i=1

 

 

 

n

= 0

(4.2)

 

∑Fiy

i=1

 

 

 

n

 

 

∑Fiz = 0.

 

i=1

 

 

Если при этом все силы системы лежат в одной плоскости Oxy, то и уравнение (в) также обратится в тождество и в системе останется два уравнения:

∑n Fix = 0

i=1

n (4.3)

∑Fiy = 0.i=1

Системы пар сил

Если система сил состоит только из пар, для каждой из которых, как известно, сумма векторов сил равна нулю, то уравнения проекций сил (а,б,в) в (7.4) оказываются тождествами.

Тогда для системы пар остаются только уравнения сумм проекций моментов пар, которые были записаны нами как уравнения (6.7):

∑mix

= 0,

 

 

= 0,

(6.5)

∑miy

∑miz

= 0.

 

71

Если при этом все силы системы лежат в одной плоскости, то равновесие системы описывается одним уравнением:

n

 

∑mi = 0.

(6.7)

i=1

Системы параллельных сил

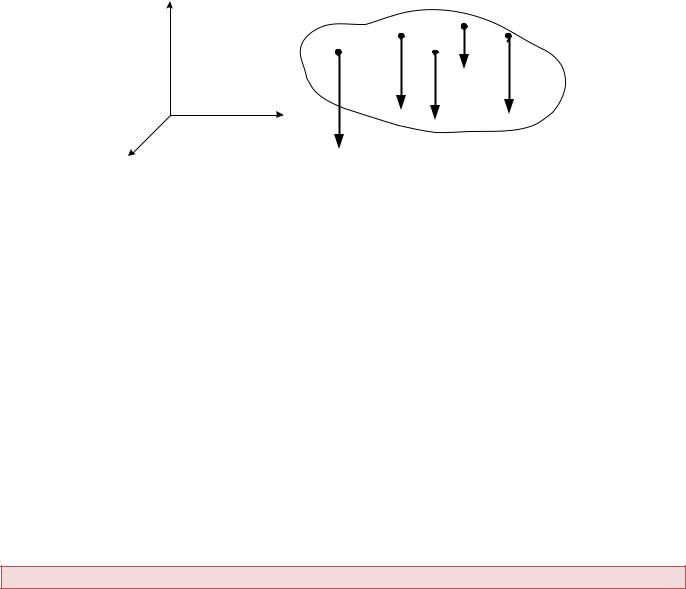
Пусть линии действия всех сил параллельны друг другу (рис. 8.4). Направим ось z параллельно этим силам. В этом случае являются тождествами уравнения проекций сил на оси х и у, а также уравнения моментов сил относительно оси z, то есть уравнения (а,б,е) из (7.4).

Тогда остаются три уравнения:

z

 

 

R

 

R

Fn

O

F2

 

R

 

 

F1

 

 

y

 

x

Рис. 8.4

∑Fiz

= 0,

 

 

n

 

 

i=1

 

 

 

n

R

 

∑M x (Fi )

i=1

 

 

 

n

R

)

∑M y (Fi

i=1

 

 

= 0,

= 0,

(8.4)

которые называются уравнениями равновесия пространственной системы па-

раллельных сил.

Тема 9.

72

ЦЕНТР ТЯЖЕСТИ

9.1. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ

Рассмотрим систему (рис. 9.1) параллельных и одинаково направленных сил

F1, F2 ,..., Fn , приложенных к твердому телу в точках O1 , O2 ,..., On .

Очевидно, что эта система сил имеет равнодействующуюкоторая имеет то же направление, что и силы системы:

R

n R

 

 

 

 

 

 

R

= ∑Fi

 

 

 

 

 

 

 

i=1

 

 

 

 

 

 

 

 

 

n

 

 

 

 

По модулю она равна

R = ∑Fi

 

 

 

 

 

 

 

i=1

 

 

 

 

Пусть единичный вектор e указывает направление сил системы. Тогда силы

можно записать в виде

 

 

 

 

 

 

 

R

R

 

 

R

 

 

F1 = F1e, F2

= F2e, ..., Fn

= Fne,

 

 

 

R

 

 

 

 

 

 

R = R ×e .

 

 

 

 

 

 

Изменим направление сил системы. Для этого с помощью единичного вектора

e′ укажем новое направление (рис. 9.1).

 

 

 

 

Тогда все силы системы повернутся на один и тот же уголα и образуется но-

 

 

′

R′

′

R′

′

R′

вая система параллельных сил F1

= F1e , F2

= F2e , ...,

Fn

= Fne , с теми же модулями,

которая имеет равнодействующую,

n

R¢ = ∑Fi = R ,

i=1

которая отличается направлением, но имеет тот же модуль.

Такую операцию будем называть поворотом системы параллельных сил.

Покажем, что имеется такая точка C , через которую линия действия равнодействующей пройдет при любом направлении сил системы.

Согласно теореме Вариньона, момент равнодействующей системы сил относительно любой точки равен сумме моментов всех сил системы относительно этой точки.

В рассматриваемом случае, например,

R ( R ) = ∑n R ( R )

MO R MO Fi

i=1

 

R

R n

R

R

или

rC

´ R = ∑(ri

´ Fi )

i=1

73

R R R

где r1 , r2 ,..., rn — радиус-векторы точек O1 , O2 ,..., On , проведенные из начала коор-

R

динат (точки O ), rC —

R

F1

R z r1

O

x

радиус-вектор точки С.

R′ e

R

R e

F1′

R

F2′

 

 

R

R

 

Fn

F2

 

 

R

 

 

r2

 

 

R

 

 

rC

R

R

 

R

R′

y

 

 

Рис. 9.1

R

Fn′

Выразим в последнем равенстве все векторы сил через единичный вектор, тогда оно примет вид:

R

R

n

R

× Fi

R

R R

 

n

R

R

rC

× R e

= ∑(ri

e )

или (RrC )×e

=

∑Fi ri

×e

 

 

i=1

 

 

 

 

i=1

 

 

Чтобы это равенство выполнялось при любом по направлению единичном векторе e должны быть равны сомножители этого вектора в левой и правой частях, т. е.

n

R = ∑ R

RrC Fi ri

i=1

откуда получаем:

 

 

n

R

 

 

 

 

 

R

=

∑Fi ri

(9.1)

i=1

 

r

 

 

 

C

 

 

R

 

 

 

 

 

Точка С, через которую линия действия равнодействующей пройдет при любом повороте системы параллельных сил, называетсяцентром параллельных сил.

Формула (9.1) определяет положение центра параллельных сил через его ра- диус-вектор.

74

Координаты центра параллельных сил можно получить, если спроектировать равенство (9.1) на координатные оси:

 

 

 

 

∑xi Fi

 

 

 

 

 

 

 

 

n

 

 

 

 

x

=

 

i=1

,

 

 

 

 

 

C

 

 

R

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

∑yi Fi

 

 

 

 

y

=

 

i=1

 

 

,

(9.2)

 

 

 

 

 

C

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

=

∑zi Fi

 

 

 

 

z

i=1

 

.

 

 

 

 

 

C

 

 

R

 

 

 

 

Заметим, что формулы (9.1) и (9.2) справедливы и для случая параллельных сил, направленных в разные стороны, если в них полагать величины Fi для сил одно го направления со знаком «плюс», а для сил другого направления со знаком «минус».

При этом, конечно, сумма сил не должна быть равна нулю.

9.2. ЦЕНТР ТЯЖЕСТИ СИСТЕМЫ ТЕЛ

Силы притяжения отдельных частиц тела к Земле направлены к центру Земли. Поскольку размеры рассматриваемых тел малы по сравнению с радиусом Земли, эти силы можно считать параллельными.

Равнодействующая этих параллельных сил — это сила тяжести (ее модуль — это вес тела), а центр этой системы параллельных сил (в котором всегда приложена сила тяжести) называется центром тяжести тела.

Поворот тела относительно Земли приводит к повороту системы сил относительно самого тела. При этом положение центра тяжести тела не зависит от расположения тела в пространстве.

Если обозначить модули сил тяжести отдельных частей тела G1 , G2 ,..., Gn , и вес

n

 

 

 

 

 

тела G = ∑Gi , то радиус-вектор и координаты центра тяжести могут быть вычисле-

i=1

 

 

 

 

 

ны по общей формуле

 

 

 

 

 

n

R

 

 

 

 

 

 

 

R

=

∑Gi ri

,

(9.3)

i=1

 

r

 

 

 

C

 

 

G

 

 

 

 

 

 

 

75

из которой следует, что

 

 

 

 

n

 

 

 

 

 

=

 

∑xiGi

 

 

 

 

x

 

i=1

,

 

 

 

 

 

C

 

 

G

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

∑yiGi

 

 

 

 

y

=

 

i=1

 

 

,

(9.4)

 

 

 

 

 

C

 

 

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

=

∑ziGi

 

 

 

 

z

i=1

.

 

 

 

 

C

 

 

G

 

 

 

 

Если тело однородное, т. е. все его части имеют один и тот же удельный вес

γ = gρ , где g −

ускорение свободного падения, а ρ − плотность, то G = γV и Gi = γVi

n

 

 

 

 

 

 

 

 

 

, где V = ∑Vi −

объем всего тела, а Vi −

объем i- ой его части.

i=1

 

 

 

 

 

 

 

 

 

После подстановки этих выражений в формулы (9.4) и сокращения мы полу-

чаем соотношения для координат центра тяжести объема:

 

 

 

 

 

n

 

 

 

 

 

 

 

 

∑xiVi

 

 

 

 

 

 

 

=

 

 

 

 

 

 

x

 

i =1

,

 

 

 

 

 

 

 

C

 

 

V

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

∑ yiVi

 

 

 

 

 

y

C

=

 

i =1

 

 

,

(9.5)

 

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

∑ziVi

 

 

 

 

 

 

 

=

 

 

 

 

 

zC

i =1

 

.

 

 

V

 

 

 

 

 

 

 

 

 

 

 

Центр тяжести однородной тонкой пластины постоянной толщины (оболочки)

— может быть вычислен аналогично через площади отдельных ее частей Ai и об-

n

щую площадь A = ∑ Ai :

i =1

76

 

 

n

 

 

 

 

 

 

=

∑ xi Ai

 

 

 

 

 

i=1

 

,

 

xC

 

A

 

 

 

n

 

 

 

 

 

 

 

∑ yi Ai

 

 

 

 

 

=

i=1

 

 

 

,

(9.6)

yC

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

=

∑ zi Ai

 

 

 

 

 

i=1

 

 

.

 

zC

 

 

 

 

A

 

Если при этом вся пластина лежит в одной плоскости, например в плоскости Oxy), то третье уравнение в (9.6) обращается в тождество и центр тяжести определяется по формулам

 

 

 

 

n

 

 

 

 

=

 

∑xi Ai

 

 

x

 

i=1

,

 

A

 

C

 

 

(9.7)

 

 

 

 

n

 

 

 

 

 

 

 

 

 

∑ yi Ai

 

 

y

=

i=1

 

.

 

 

 

C

 

 

A

 

 

 

 

 

 

 

 

Центр тяжести однородного пространственного ломаного стержня, состоящего из ряда прямолинейных участков, определяется через длины его участков Li и

n

 

 

 

 

 

 

 

общую длину L = ∑Li

:

 

 

 

 

 

 

i=1

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

=

∑ xi Li

 

 

 

 

 

i=1

 

,

 

xC

 

 

 

 

L

 

 

 

n

 

 

 

 

 

 

 

∑ yi Li

 

 

 

 

 

=

i=1

 

 

 

,

(9.8)

yC

 

 

 

 

L

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

=

∑ zi Li

 

 

 

 

 

i=1

 

 

.

 

zC

 

 

 

 

L

 

77

КИНЕМАТИКА

1.Тема:

КИНЕМАТИКА ТОЧКИ

1.1.ВВЕДЕНИЕ В КИНЕМАТИКУ

Кинематикойназывается раздел механики, в котором изучаются движения материальных тел без учета их масс и действующих на них сил, то есть с чисто геометрической точки зрения.

Под движением в механике понимают изменение положения данного тела в пространстве по отношению к некоторой координатной системе, которую называют си-

стемой отсчета.

Таким образом, понятие движения является относительным. Тело, находящееся в покое относительно одной системы отсчета может совершать движение относительно другой системы отсчета.

Пространство в классической механике считается однородным, изотропным и евклидовым, а время является абсолютным, то есть протекающим одинаково во всех системах отсчета.

Для описания течения времени в механике используют независимую переменную − время. При этом все другие переменные величины рассматривают как функции времени. Отсчет времени ведут от некоторого начального момента .

Основной задачей кинематики является изучение способов задания движения тел. Движение тела считается заданным, если для любого момента времени можно математически указать положение любой точки тела по отношению к данной системе отсчета.

Для описания движения кинематика кинематика использует кинематические характеристики, такие как скорости или ускорения, и устанавливает связывающие их математические зависимости.

Основными разделами кинематики являются:

∙кинематика точки,

∙кинематика твердого тела,

∙сложное движение точки,

z

78

∙ сложное движение твердого тела.

1.2.СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

В кинематике используют три способа задания движения точки: векторный, координатный и естественный.

Векторный способ задания движения точки

Положение движущейся точки М по отношению к системе отсчета Оxyzможно задать радиус-вектором этой точки , который считается векторной функцией времени:

(1.1)

M

R

r

R k

j

O

z

y

R

 

i

x

 

x

y

 

 

Рис. 1.1

Уравнение (1.1) представляет собой уравнение движения точки в векторной

форме. Линия, которую описывает точка в своем движении, называется ее траек-

торией точки.

 

Траектории движения точек можно разделить на прямолинейные и криволиней-

ные.

 

Конец радиус-вектора указывает на точку М и в процессе движения всегда заканчивается на её траектории.

Таким образом, траектория точки является годографомвектора .

Координатный способ задания движения точки

79

 

Положение точки в данной системе отсчета можно определить, задав ее коорди-

 

 

 

 

,

 

 

(1.2)

наты в виде функций времени. В декартовой системе координат это будут функции

 

 

 

 

,

 

 

 

 

Эти уравнения .

 

 

 

 

 

 

 

можно рассматривать как уравнения траектории точки, заданные

в параметрической форме. Время

 

в данном случае будет являться параметром.

Чтобы получить уравнение

траектории в явной форме надо из уравнений (1.2) ис-

 

 

 

 

ключить время.

 

 

 

 

 

 

Связь между векторным и координатным способами задания движения точки да-

 

 

 

 

 

 

,

(1.3)

ется формулой

 

 

где

,

,

единичные вектора (орты) декартовой системы координат.

 

–

Естественный способ задания движения точки

Этот способ применяется когда заранее известна траектория точки.

 

A

−

O +

M

 

 

 

 

 

 

 

     

 

 

 

 

s

 

 

 

 

 

B

 

 

 

Рис. 1.2

 

Чтобы задать движение некоторой точки М естественным способом, следует

указать:

 

 

 

1.

траекторию точки (кривая АВ на рис. 1.2);

 

2.

начальную точку на ней (точкаО на рис. 1.2);

 

3.

положительное и отрицательное направление отсчета по траектории;

в котором s

,

 

 

4.

уравнение движения точки по траектории:

 

 

 

 

 

(1.4)

есть дуговая координата, то есть длина дуги по траектории между точкамиО и М, взятая со знаком «плюс» или «минус» в зависимости от того в какой части траектории находится точка.

Дуговая координата определяет положение точки на траектории движения, а не пройденный ею путь.

1.3.СКОРОСТЬ ТОЧКИ

Определение скорости при векторном способе задания движения

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности