
8508
.pdf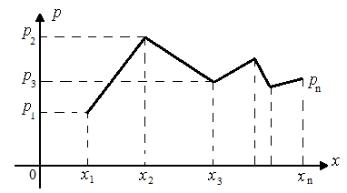
Рис. 1.1. Многоугольник распределения дискретной величины
Для случайной непрерывной величины невозможно говорить о вероятности значения случайной величины в точке P( X = x) , но можно определить вероятность ее значения в любом интервале области возможных значений
X = {(a, b)} − a b + . |
|
Функцией распределения случайной величины X |
называется функ- |
ция FХ (x) , выражающая для каждого числа x из области возможных значений вероятность того, что случайная величина X примет значение, меньшее этого числа:
F(x) = P( X x) , x Х .
Функция распределения F (x) принимает значения на отрезке [ 0;1] , т.к. ее значения есть вероятность события. Она будет рассматриваться как непрерывная и дифференцируемая функция, обладающая следующими важными свойствами:
P(x1 X x2 ) = F (x2 ) − F (x1 ) ,
F (x2 ) −
F(x1)
0
, т.е. F (x2 ) F (x1) при x2 x1 .
F (õ) →0, |
F (x) →1 |
. |
õ→a+0 |
x→b−0 |
Таким образом, функция распределения F (x) не убывает, её значения расположены на отрезке [0;1] . При стремлении x → а функция распределения обращается в ноль, а при стремлении x → b функция распределения обращается в единицу. Примерный график функции распределения F (x) приведён на рис. 1.2.
61
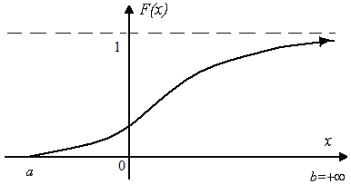
Рис. 1.2. Функция распределения случайной непрерывной величины
Пусть имеется непрерывная случайная величина, определённая в области = {( , )}, −∞ < < < +∞, и описывается непрерывной и дифференцируемой функцией распределения ( ). Вычислим вероятность нахождения случайной величины в h -интервале и поделим ее на
длину интервала: |
|
|
|
|
|
|
|
( ≤ ≤ + ) |
= |
( + ) − ( ) |
→ |
′( ). |
|
|
|
|
|
|||
|
|
|
→0 |
|||
Такие величины называются обычно погонной плотностью или просто плотностью величины. Плотностью распределения вероятностей (или сокращённо плотностью вероятности) непрерывной случайной величины называется производная от её функции распределения: ( ) =
′( ).
Плотность вероятности обладает рядом замечательных свойств:
|
b |
|
|
|
|
f (x) 0 , |
|
f (x) dx = 1 , |
f (x) →0 |
, |
|
|
|
|
x→a,b |
|
|
|
a |
|
|
|
|
|
|
x |
|
x |
|
|
|
2 |
|
|
|
P(x1 X x2 ) = |
f (x) dx , |
F (x) = f (t) dt . |
|||
|
|
x1 |
|
a |
|
В силу указанных свойств, функция ( ) плотности распределения вероятностей всегда неотрицательна, стремится к нулю на границах области возможных значений, вероятность нахождения в интервале значений величины равна площади под графиком функции ( ) , опирающейся на интервал значений, а вся площадь между графиком функции ( ) и осью абсцисс равна единице. Примерный график функции ( ) плотности распределения вероятностей изображён на следующем рис.
1.3.
62

Рис. 1.3. Свойства функции распределения и плотности распределения
Итак, для полной характеристики случайной величины достаточно знать или функцию распределения, или плотность распределения вероятностей (т.к. одну из них можно выразить через другую):
x F (x) = f (t) dt
a
или
f (x) =
F '(x)
.
Вероятностная модель наблюдаемого явления создается именно в виде случайной величины или системы случайных величин с заданными областями их возможных значений и законами распределения.
Часто, особенно в задачах математической статистики, удобнее использовать не функцию распределения F (x) , а обратную к ней функцию Fobr ( p) , которая, как и сама функция распределения является монотонной, однозначной и непрерывной функцией от вероятности. Так для выделения части области возможных значений X , где случайная величина может находиться (принимать эти значения в опыте) с той или иной заданной вероятностью, используются квантили распределения по заданному уровню вероятности.
Левосторонняя квантиль
аправосторонняя
b |
|
P( X xα ) = |
f (x) dx = α . |
x |
|
α |
|
xβ |
= Fobr (β) определяется как P( X |
|
|
квантиль |
xα = Fobr (1− α) |
xβ
xβ ) = f (x) dx = β ,
a
определяется
63
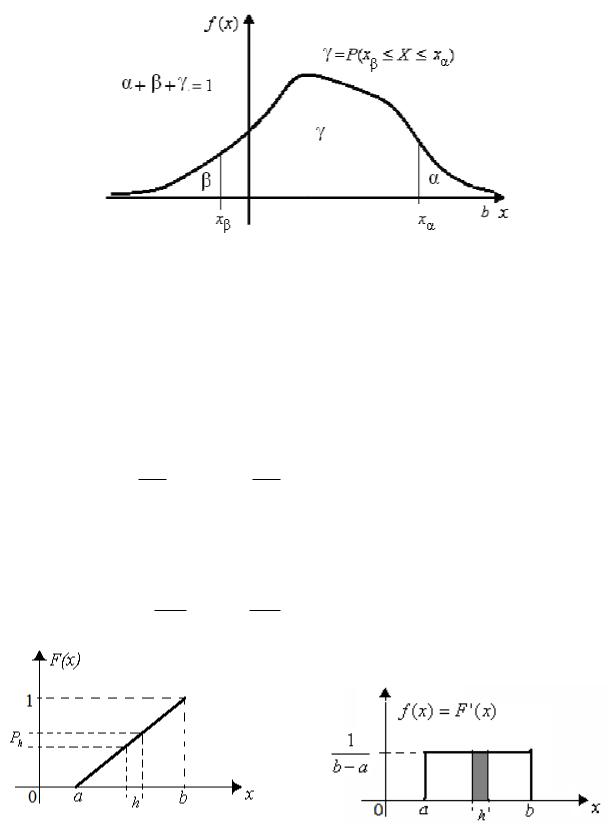
Рис. 1.4. Левосторонняя и правосторонняя квантили распределения
Обе эти квантили используются для отсечения приграничных частей у области возможных значений X = {(− ,+ )} рис. 1.4, а для выделения срединной части области часто используется центральная квантиль, где случайная величина будет находиться с вероятностью γ . Границы центральной квантили, за которые случайная величина выходит с равной вероят-
ностью α = β = (1− γ) / 2 :
xγ1 = Fobr (1−2 γ ) ,
x |
= F |
1+ γ |
) |
( |
|||
γ2 |
obr |
2 |
|
|
|
|
,
xγ 2 P(xγ1 X xγ 2 ) = xγ1
f (x) dx =
γ
.
Пример. Рассмотрим случайную непрерывную величину, определённую на конечном отрезке с линейно нарастающей функцией распределения рис. 1.5.
F (x) =
x − a b − a
,
f (x) = |
1 |
|
b − a |
||
|
, x X = {(a, b)} |
− a b + |
Рис. 1.5. Функция распределения равномерной случайной величины
Вычисляя вероятность попадания случайной величины в интервал длиной h , получим, что Ph = P(x X x + h) = F (x + h) − F (x) = h /(b − a) , то есть эта вероятность постоянна и не зависит от расположения h интервала в
64

области X , а зависит лишь от длины интервала. Такая величина, принимающая свои значения с равной вероятностью во всех точках области возможных значений, называется равномерной случайной величиной.
Это может быть, например, время ожидания трамвая на остановке при регулярном их движении с периодом Т.
Обратная функция распределения и квантили для такого распределения следующие:
Fobr ( p) = a + p(b − a) ,
xβ
=
F |
(β) |
obr |
|
, xα = Fobr (1− α) .
3.1.2. Числовые характеристики случайных величин
Закон распределения случайной величины, заданный в той или иной форме, полностью определяет случайную величину как некоторую модель наблюдаемого в опыте явления. Однако часто в практической деятельности знание закона бывает невозможным, а то и избыточным, достаточно знать лишь некоторые общие (интегральные) характеристики
случайной величины. |
|
Пусть случайная величина |
X , дискретная или непрерывная, зада- |
ется законом распределения, тогда основными характеристиками случайной величины являются:
Математическое ожидание:
|
|
|
xk |
pk |
− для |
дискретной случайной величины |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
M ( X ) = mX |
= |
xf X (x)dx |
− для |
непрерывной случайной величины |
||
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
Дисперсия:
|
|
|
(xk |
− mX )2 pk |
− для |
дискретной случайной величины |
D( X ) = DX |
|
|
m |
|
|
|
= |
(x − mX )2 f X (x)dx |
− для |
непрерывной случайной величины |
|||
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
Среднеквадратическое отклонение:
σ(X ) = σX = 
 DX .
DX .
Математическое ожидание М ( X ) = mX характеризует центр распределения или средневзвешенное ожидаемое значение величины, а геометрически оно изображается как координата центра тяжести фигуры,
65
образованной осью |
х |
и линией функции |
f (х) или p(хm ) . Дисперсия |
|
D(X ) = x |
характеризует средний ожидаемый разброс (широту, изменчи- |
|||
2 |
|
|
|
|
вость, вариативность) значений величины возле М ( X ) , поскольку совпадает с математическим ожиданием квадрата отклонения случайной величины от его математического ожидания.
~ |
2 |
) , где |
~ |
= X − mX . |
D(X ) = M (X |
X |
|||
|
|
|
|
|
Среднеквадратическое отклонение (X ) = x |
имеет тот же смысл, что и |
|||
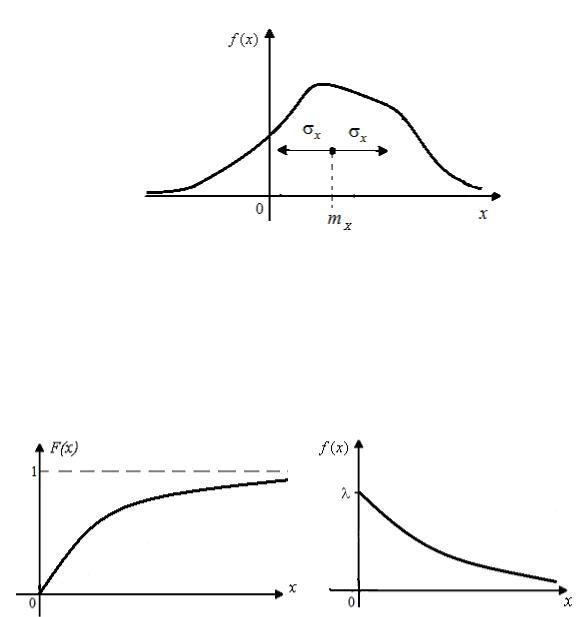
дисперсия, но в отличие от неё имеет размерность, совпадающую с размерностью самой случайной величины, что более удобно и позволяет изобразить его, как и математическое ожидание, на рис. 1.6. Между дисперсией и математическим ожиданием имеется простая связь
D( X ) = M ( X 2 ) − M 2 ( X ) .
М ( X )
=
Рис. 1.6. Геометрическая иллюстрация понятий математического ожидания
mX |
и дисперсии D(X ) = 2 |
случайной величины |
|
x |
|
Пример. Рассмотрим случайную величину X , определенную на мно-
жестве возможных значений Х |
= {[0;+ )} со следующим законом распре- |
||||||
деления FX |
(x) =1−e |
−λx |
, |
fX |
(x) = λ e |
−λx |
, где параметр λ 0 . Такая случайная не- |
|
|
|
|
|
|
||
прерывная величина называется показательной (рис. 1.7).
66

Рис. 1.7. Функция распределения |
FX (x) и плотность распределения |
f |
|||||||||||||||||||||||||
ной случайной величины |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
M ( X ) = x e |
−x |
dx = − x e |
−x |
+ e |
−x |
dx |
= |
0 − |
|
e |
−x |
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M ( X 2 ) = x2 e− x dx = −x2 e− x |
|
x e−xdx = 0 − 2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D( X ) = M ( X |
2 |
) − M |
2 |
( X ) = |
2 |
|
− |
1 |
2 |
= |
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X (x) |
показатель- |
|||
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
2 |
|
|
|
|
|
|
|
|
|
2 |
||
Математическое ожидание постоянной величины равно этой постоянной величине, а её дисперсия равна нулю:
X = C =const M ( X ) = C , D( X ) = 0 .
Умножение случайной величины на постоянный множитель приводит к следующему изменению её характеристик:
M (C X ) = C M ( X ) , D(С X ) = С |
2 |
D( X ) , где C = const. |
|
|
Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий этих величин:
M ( X1 + X 2 + + X k ) = M ( X1 ) + M ( X 2 ) + + M ( X k ) . |
|||
Из вышеприведённых свойств можно заметить, что при преобразо- |
|||
вании случайной величины X по линейному закону в величинуY |
|||
Y = |
X − m |
M (Y ) = 0, D(Y ) = 1 . |
|
|
X |
||
|
|
|
|
|
σ |
X |
|
|
|
|
|
Такое преобразование случайной величины называется центрированием и нормированием, а характеристики получаемой величины называются стандартными.
Для независимых случайных величин X и Y имеет место:
( + ) = ( ) + ( ), ( ) = ( ) ( ).
Величины называются независимыми, если распределение любой из них не зависит от того, какие значения принимает другая величина. В противном случае величины являются статистически зависимыми.
3.1.3. Нормальная случайная величина
Случайная величина имеет нормальный закон распределения (за-
кон Гаусса), если она определена в области Х = {(−;+ )} , а её плотность распределения вероятностей имеет вид:
67

|
|
1 |
|
− |
( x−m) |
2 |
|
|
f (x) = |
e |
|
||||
|
|
|
|
||||
|
|
|
2σ |
2 |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
σ |
2 |
|
|
|
|
|
где m |
и - параметры распределения (σ 0, − m + ). |
||||||
Нормальный закон распределения X = N (m, σ) наиболее часто встречается на практике. Главная его особенность – он является предельным законом, которым приближаются другие, более сложные законы распре-
деления . |
|
|
|
|
Плотность вероятности f (x) похожа на «колокол» (рис. 1.8). |
|
|
||
При уменьшении только параметра |
|
, график функции сжимается и под- |
||
нимается вверх по оси ординат. При изменении только параметра |
m |
, |
||
|
|
|
|
|
график перемещается вдоль оси абсцисс.
Рис. 1.8. Функция плотности распределения нормальной величины
Функция распределения F (x) нормальной величины имеет вид:
x |
|
|
|
x |
−(t −m) |
2 |
|
|
|
|
|
x |
u 2 |
|
|
|
1 |
|
1 |
+ ( x − m) , где (x) = |
1 |
|
|||||||
F (x) = |
f (t) dt = |
|
e |
2σ2 |
dt = |
|
e− |
|
|
|||||
|
|
2 du |
||||||||||||
|
|
|
|
|
|
|
||||||||
− |
|
σ |
2π |
− |
|
|
2 |
σ |
|
2π 0 |
|
|
||
|
|
|
|
|
|
|
|
|||||||
График функции распределения F (x) |
изображен на рис. 1.9. |
|
|
|
|
|||||||||
Рис. 1.9. Функция распределения нормальной величины
68

Вероятность того, что изучаемая случайная величина (распределённая
нормально) примет значение в пределах от x1 |
до x2 |
вычисляется по фор- |
||||||||||
муле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − m |
|
x |
|
x |
|
− m |
|
x − m |
|
|
P(x1 |
X x2 ) = ( |
) |
2 |
= ( |
|
) − ( |
) . |
|||||
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
σ |
|
x |
|
|
|
σ |
|
|
σ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
В частном случае, когда интервал симметричен относительно мат.ожидания m , эта формула выглядит так:
P(m − ε X m + ε) =
P( X
X
− m ε) =
ε) =
2
ε σ
.
Рассмотрим вероятность того, что изучаемая случайная (распределённая нормально) примет значение в пределах от
m + 3σ :
величина m − 3σ до
P(m −3σ X
m + 3σ) =
2 (3σ/σ) = 2 (3)
0,9973
,
т.е. вероятность значений изучаемой случайной величины именно на
интервале |
[m −3σ, m + 3σ] |
велика. Это утверждение составляет правило |
«трёх сигм». Числовые характеристики нормальной случайной величины
:
2 |
. |
М ( X ) = m , D( X ) = σ |
Пример. Наблюдение за скоростью автомашин на определённом участке дороги показало, что скорость есть нормальная случайная величина с математическим ожиданием 60 км/ч и среднеквадратическим отклонением 10 км/ч. Определить вероятность того, что:
-скорость на этом участке не превышает 80 км/ч,
-скорость не отклоняется от мат.ожидания более чем на 20%. Поскольку скорость есть нормальная величина с параметрами
m = 60 |
и σ =10 |
, то по основным формулам находим: |
P(0 V
80) = ( x − m)
σ 20% 60 =12
80 |
|
|
80 − 60 |
|
|||
|
= ( |
) |
|||||
0 |
10 |
||||||
|
|
|
|||||
|
|
|
|
|
|
||
P( |
|
V − 60 |
|
12) |
|||
|
|
||||||
|
|
|
|
|
|
|
|
− ( |
0 − 60 |
) |
|
|
|||
|
10 |
|
|
|
12 |
) = |
|
= 2 ( |
|||
|
10 |
|
|
= (2) − (−6) = 0, 477 + 0,5 = 0,947 ,
2 (1, 2) = 2 0,385 = 0, 770 .
Вычислим скорость, которую автомашины на этом участке не превышают с вероятностью 0,99. Из уравнения
P(0 V vm ax ) = ( x − m) |
vmax |
= (vmax − 60) − (0 − 60) = (vmax − 60) − (−6) = 0,99 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
0 |
10 |
|
10 |
10 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
vmax − 60 |
) = 0, 49 |
|
vm ax − 60 |
|
= 2,33 vm ax = 60 +10 2,33 = 83,3 . |
||||||||
|
||||||||||||||
|
|
|||||||||||||
10 |
|
|
|
|
10 |
|
|
|
|
|
|
|||
69
Нормальная случайная величина X = N (m, σ) обладает рядом исключительных свойств, важнейшим из которых является центральное утверждение закона больших чисел о том, что если мы имеем систему n случайных величин, X i с конечными мат.ожиданиями и дисперсиями mi , i2 то величина
|
n |
|
|
|
|
|
Y = |
|
X |
→N(m |
, |
) |
|
n |
i |
n→ |
n |
n |
|
|
|
i=1 |
|
|
|
|
|
где
n |
|
n |
|
i |
|
m |
= |
m |
|
|
i=1 |
,
n |
n |
= i |
|
2 |
2 |
|
i=1 |
.
Это означает, что чем сложней случайная величина, чем больше случайных факторов влияет на ее значение, тем больше она приближается к нормальной случайной величине.
3.2 Основные задачи и методы математической статистики
Для установления закономерностей, которым подчинены случайные события и случайные величины, теория вероятности, как и любая другая наука, обращается к опыту – наблюдениям, измерениям, экспериментам. Результаты наблюдений за случайными величинами объединяются в наборы статистических данных. Задачей математической статистики, раздела современной теории вероятностей, является разработка методов сбора и обработки статистических данных, а также их анализа и синтеза с целью установления законов распределения наблюдаемых случайных величин.
Выборочный метод. Генеральной совокупностью является набор всех мыслимых статистических данных, при наблюдениях случайной величины:
х |
Г |
= {х |
, х |
2 |
, х |
3 |
,......, |
|
1 |
|
|
|
х |
N |
} = {x |
; i |
|
i |
|
=1,
N}
.
Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность есть статистический аналог случайной величины, её объем N обычно велик, поэтому из неё выбирается часть данных, называемая выборочной совокупностью или просто выборкой
х |
B |
= {х |
, х |
2 |
, х |
3 |
,......, х |
n |
} = {x |
; i = 1, n} |
, |
х |
В |
х |
Г |
, n N |
. |
|
1 |
|
|
|
i |
|
|
|
|
Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать её сплошного (массового) наблюдения, что часто бывает ресурсоёмким процессом, а то и просто невозможным. Однако выборка должна удовлетворять следующим основным требованиям:
70
