8508

ного сигнала иногда используются полиномы первого порядка. В этом случае между моментами отсчёта непрерывный сигнал ( ) аппроксимируется линейной функцией. Соответствующие формулы могут быть легко получены самостоятельно. Устройство, обеспечивающее восстановление сигнала на основе полинома первого порядка, называется эк-

траполятором первого порядка (First-Order Hold, FOH). Заметим, что ин-

терполяционные полиномы выше первого порядка практически не используются для восстановления непрерывного сигнала, поскольку могут отрицательно сказаться на устойчивости систем с управлением.

2.3.2. Синтез регулятора при полной информации о состоянии

Рассмотрим теперь построение цифровой системы управления в задаче стабилизации перевёрнутого маятника. Сделаем упрощающие предположения. Во-первых, при преобразовании непрерывного сигнала в дискретный используется только дискретизация по времени с интервалом дискретизации ; во-вторых, в моменты отсчёта = ,+, известно состояние объекта, то есть вектор = , , ̇, ̇ , и, в- третьих, для преобразования дискретных значений управления в непрерывную функцию используется экстраполятор нулевого порядка:

Динамика маятника в окрестности неустойчивого положения равновесия описывается линейной системой дифференциальных уравнений (2.7), а регулятор, как следует из соотношения (2.27), является дискретным, поэтому для синтеза цифровой системы управления нужно перейти к описанию объекта управления в виде системы разностных уравнений, эквивалентной исходной системе (2.7). Эквивалентность здесь понимается в том смысле, что при одинаковых начальных условиях и управлениях вида (2.27) состояния непрерывной и эквивалентной систем совпадают в моменты отсчёта . Запишем решение системы (2.7):

Положим = (+1) и учтём, что согласно равенству (2.27) управление ( ) можно вынести за знак интеграла. После этого выражение (2.28)

51

примет вид

Упрощая интеграл и вводя обозначение = ( ), приходим к эквивалентной дискретной системе

Таким образом, задача синтеза цифрового стабилизирующего регулятора для непрерывной системы (2.7) свелась к задаче стабилизации дискретной системы (2.29). Поскольку по предположению в моменты отсчёта = , +, известно состояние объекта (2.29), то управлениебудем искать в классе линейных обратных связей по состоянию, то есть

Заметим, что уравнение (2.29) по форме «совпадает» с системой (2.7), поэтому задача синтеза стабилизирующего регулятора для системы (2.29) может быть решена теми же методами, которые применялись в предыдущих разделах при синтезе непрерывных регуляторов.

Для проведения численных расчётов, положим = 0.1, тогда

В этом случае система (2.29) является полностью управляемой, так как

Следовательно, существуют такие матрицы обратной связи Θ, что все собственные числа матрицы замкнутой системы + Θ лежат внутри единичного круга комплексной плоскости, то есть замкнутая система

52

является устойчивой. Для построения такой матрицы Θ воспользуемся алгоритмом модального управления из раздела 2.2.1.

Матрица имеет собственные числа

поэтому внутрь единичного круга достаточно передвинуть только 3 и4. Выберем в качестве новых значений ′3 = − 2 и ′4 = − 1. Построим преобразование, приводящее матрицу к блочной нижнетреугольной форме так, чтобы в начале главной диагонали располагались числа 3 и4. Для этого найдём левые собственные векторы 3 и 4, соответствующие собственным числам 3 и 4, и дополним их произвольными векторами, например базисными векторами 1 и 2, до линейно независимой системы, тогда матрица преобразования запишется как

Определим параметры 1 и 2 так, чтобы ′3 и ′4 являлись корнями характеристического многочлена выделенного блока матрицы , то есть

2 − 2.892 + 0.013 1 − 0.043 2 + 1.892 + 0.025 1 − 0.043 2 = 0.

53

Применяя к многочлену теорему Виета, приходим к системе

2.892 + 0.013 1 − 0.043 2 = 0.858, 1.892 + 0.025 1 − 0.043 2 = 0.174,

На рисунке 2.12 приведены графики изменения компонент вектора состояния и управления в зависимости от времени. Для линейной системы (2.7), замкнутой регулятором (2.32), соответствующие кривые изображены красным цветом, а для нелинейной системы (2.4) при использовании этого же регулятора — синим цветом. Из представленных графиков видно, что при сравнительно небольших отклонениях маятника от вертикального положения построенный дискретный регулятор является стабилизирующим для нелинейной системы (2.4).

Для сравнения рассмотрим случай, когда интервал дискретизации= 0.5. Матрица имеет неустойчивые собственные числа 3 = 1 и4 ≈ 24.230. Также как и в предыдущем случае, передвинем их внутрь единичного круга в точки ′3 = − 2 и ′4 = − 1. Нетрудно получить, что матрица параметров регулятора равна

переходных процессов в системах (2.7) и (2.4), замкнутых регулятором (2.33), приведены на рисунке 2.13. Из представленных графиков видно, что при начальных условиях 0 = (0.0, −0.3, 0.0, 0.0) добиться стабилизации перевёрнутого маятника не удаётся. Однако, легко проверить, что стабилизация возможна при начальных условиях 0 = (0.0, −0.1, 0.0, 0.0) . Сравнивая начальные условия в этом и предыдущем примерах, заключаем, что увеличение интервала дискретизации может привести к уменьшению области притяжения равновесного состояния (0, 0, 0, 0) нелинейной системы (2.4), замкнутой регулятором

(2.33).

54

Рис. 2.12. Графики зависимости от времени смещения и скорости ̇тележки, угла отклонения и угловой скорости ̇маятника и управления для линейной (красный цвет) и нелинейной (синий цвет) систем, замкнутых регулято-

ром (2.9); начальные условия 0 = (0.0, −0.6, 0.0, 0.0) .

55

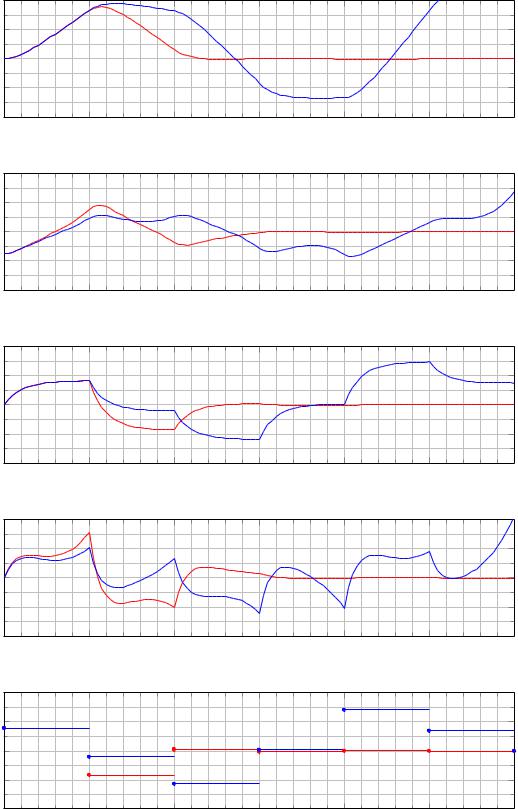
Рис. 2.13. Графики зависимости от времени смещения и скорости ̇тележки, угла отклонения и угловой скорости ̇маятника и управления для линейной (красный цвет) и нелинейной (синий цвет) систем, замкнутых регулято-

ром (2.9); начальные условия 0 = (0.0, −0.3, 0.0, 0.0) .

56

3. Элементы математической статистики

Вероятностный подход к изучению сложных и неподдающихся обычному динамическому описанию явлений появился и развивался в силу необходимости описать, понять и предсказать подобные явления. Таких непредсказуемых, содержащих элемент случайности, явлений в различных сферах человеческой деятельности большинство. Это явления от игры в кости или хаотического движения части газов до социальнопсихологических явлений в обществе. Иметь вероятностную (стохастическую) модель явления, это все лучше, чем не иметь никакой модели и сдаться перед сложностью явлении. Теория вероятностей создает и исследует модели случайных явлений, а с другой стороны, ее раздел Математическая статистика, на основе наблюдений за явлением анализирует и консолидирует эти данные для создания и уточнения вероятностной модели.

Задачи статистического анализа очень часто встречаются в различных областях научно-практической деятельности человека. Эти задачи связаны со сбором и обработкой наблюдательных данных над теми или иными объектами, явлениями или процессами. Под наблюдениями понимается довольно широкое понятие, включающее в себя получение наборов статистических данных различного свойства и форматов. Объекты таких наблюдений могут иметь различную природу, это, например, экспериментальные измерения в научно-технических установках, экс- плуатационно-технические проверки и акты, геологические паспорта территорий, финансово-экономические отчеты, регистрационно-ка- дастровые документы, социально-политические опросы, медико-психо- логические обследования и многое другое. Обработка статистических данных связана с анализом и выявлением закономерностей в поведении объектов с целью объяснений наблюдений, выявления причин и предсказания поведения наблюдаемых объектов.

Вобласти строительства также имеется ряд задач по обработке и анализу о свойствах строительных материалов и конструкций, отраженных в текущих и аттестационных поверочных измерениях, отчетах о себестоимостях строительства объекта и его содержания, о состоянии инфраструктурных элементов.

Всвязи со столь широким предметом исследования статистика превратилась из наблюдательно-фиксирующей науки в аналитическую с

57

широчайшим применением математических методов планирования, сбора и обработки статистических данных. Наблюдаемые величины всегда в той или иной степени являются непредсказуемыми, то есть случайными. Случайность измеряемых величин связана как с их внутренней стохастичностью, так и с ошибками измерения, вносимыми прибором и измеряющим субъектом. Методы теории вероятностей и математической статистики лежат в основе всех методов статистического анализа.

К задачам статистического анализа обычно относят следующие задачи:

▪корреляционный анализ (определение зависимости величин),

▪регрессионный анализ (определение формы зависимости),

▪дисперсионный анализ (анализ влияния условий измерения),

▪факторный анализ (определение наиболее значимых факторов),

▪кластерный анализ (классификация и идентификация объектов),

▪дискриминантный анализ (выбор наилучших решений),

▪анализ временных рядов (обработка изменяющихся во времени данных, их сглаживание и прогноз),

▪планирование эксперимента (анализ мероприятий, необходимых для достижения максимальной точности измерений и достоверности выводов),

▪фрактальный анализ (выделение внутренних структур в объектах).

3.1. Случайные величины

Теория вероятностей - математическая наука о случайных явлениях окружающего нас мира, имеющая серьезное эмпирическое обоснование. Случайность, как неоднозначность и непредсказуемость явлений обусловлена их сложностью или их квантовой сущностью, а также субъективным действием или восприятием человека. Рассмотрим Опыт как любое наблюдение (созерцание, измерение или эксперимент) случайного явления в произвольной практической деятельности человека, например, в бытовой, научно-познавательной, производственно-техни- ческой, социально-экономической, психофизической или какой-либо другой сфере деятельности. Событием будем называть любой возможный исход опыта. Множество всех событий опыта образуют его событийное пространство. События в опыте могут быть как равносильными, так

58

и неравносильными с точки зрения их наступления в опыте. Числовая величина, характеризующая возможность наступления события в опыте называется вероятностью события. Определение (вычисление) вероятности события производится обычно через его частоту наблюдения при массовом повторении опыта, без изменения условий проведения. Иногда, в случае наличия симметрии опыта, возможно определение теоретической (до опытной) вероятности, через число равновозможных исходов опыта, приводящих к наступлению события. Например, пусть событие, состоящее в выпадении «шестерки» в опыте по бросанию игровой кости, тогда Р( ) = 1/6 есть теоретическая вероятность события при бросании правильной кости (симметричной без смещения центра тяжести). Если кость неправильная (изношенная, специально изготовленная), то можем определить только частоты события 36 ( A) = 5 / 36 , 72 ( A) = 9 / 72 , .., при 36, 72, .. однотипных бросаниях такой кости. Но если отклонения (вариативность) этих частот с ростом числа бросаний уменьшаются, то это означает, что мы с определенной точностью вычислим эмпирическую (статистическую) вероятность события.

Другим важнейшим понятием теории вероятностей, после понятия события, является понятие случайной величины.

3.1.1. Понятие и описание случайных величин

Внимательно анализируя опыт, можно заметить, что помимо событий в опыте обычно можно увидеть и ввести некоторую числовую величину, которая своими значениями описывает все множество событий опыта. Например:

I - число, выпадающее на игральной кости. {1,2,3,4,5,6} N - число посетителей сайта за сутки. {1,2,3, . . . }

TS - время работы устройства до первого сбоя. {[0; +∞)}

Случайной величиной называется числовая величина, принимающая в опыте случайным образом одно и только одно значение из всех своих возможных значений. Будем обозначать случайные величины большими латинскими буквами X , Y , Z ,..., а их возможные значения малыми x, y, z, .

Множество всех возможных значений случайной величины X будем обозначать X = {x} , в зависимости от вида этого множества

59

случайные величины делятся на дискретные и непрерывные. Дискретная величина принимает конечное или бесконечное, но счетное, число значений

= { 1, 2, . . . , , . . . },

а непрерывная величина принимает значения из конечного или бесконечного непрерывного числового интервала

скольку каждое значение есть события А = (X = x) , В = (X x) и др. В связи

с этим необходимо уметь вычислять вероятности этих событий, то есть вероятность того, что случайная величина принимает те или иные значения.

Законом распределения PX (x) случайной величины называют любое правило (функция, таблица, график, алгоритм,..), которое устанавливает соответствие между возможными значениями случайной величины и вероятностями, с которыми она принимает эти значения.

личину как вероятностную модель случайного явления, наблюдаемого в опыте.

Поскольку у случайной дискретной величины все значения можно перечислить, то ее закон распределения удобно задавать в виде таблицы вероятностей для упорядоченных значений величины:

Получается так называемый ряд распределения случайной дискретной

p1 + p2 + p3 + + pn = pk =1.

k

Закон распределения случайной дискретной величины может быть задан и функционально в виде pm = p(xm ) , а часто в графическом виде в форме так называемого многоугольника распределения вероятностей

случайной дискретной величины, изображенного на рис. 1.1.

60