
8337
.pdf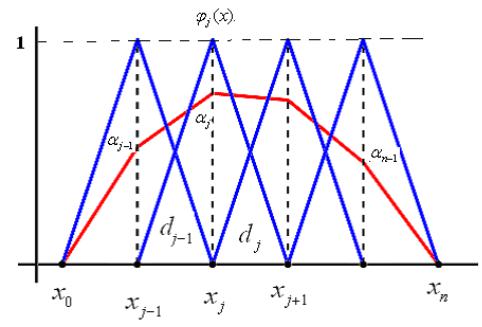
31
|
x x j 1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
x j |
x j 1 |
|||
|
|
|
x |
||
|
x j 1 |
||||
j |
(x) |
|
|
|
|
|
|
x j |
|||
|
x j 1 |
||||
|
0 |
|
x |
||
|
|
|
|
||
x j 1 x x j
x j 1 x x j x j 1; x x j 1x0 xn
Используя такие линейные конечные элементы и представив приближенное решение в виде:
n
u(x) j j (x) можно используя например метод Галеркина найти
j 1
неизвестные коэффициенты разложения i . При этом необходимо вычислить матрицу B (L k , r ) и вектор C ( f , r ) . Матрица В в силу структуры
выбранных конечных элементов будет трех диагональной и поэтому для решения системы линейных уравнений можно воспользоваться методом прогонки.
32
Система уравнений с трех диагональной матрицей для вектора ( i ) имеет вид:
ai i 1 bi i ci i 1 fi , |
i 1, 2,..n; |
a1 0, |
cn 0 , |
а ее решение путем прямой и обратной прогонки будет следующим:
На прямой прогонке определяются вспомогательные коэффициенты i 1, i 1
|
|
c1 |
, |
|
|
f1 |
, |
|
|
|
ci |
, |
|
|
fi |
i ai |
, |
i 1, 2,3,..n 1, |
|
1 |
|
i 1 |
|
i 1 |
|
|
|||||||||||
1 |
|
b1 |
|
|
b1 |
|
|
bi i ai |
|
|
bi |
i ai |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а на обратной прогонке находятся искомые коэффициенты i
|
|
|
fn |
n an |
|
|
|
|
|
|
|
, |
i n 1,..3, 2; |
n |
|
|
i |
i 1 |
i 1 |
||||||||
|
|
bn |
n an |
|
|
i 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Прогонка надежно работает при любом шаге сетки, но при выполнении следующих условий
ai 0, ci 0 , |
|
bi |
|
ai ci , |
|
|
|||
c1 / b1 0, an / bn 1, |
c1 / b1 an / bn 2 . |
|||

33
§2.2 Численное решение начально-краевых задач методом сеток.
1.Дифференциальная задача для уравнения переноса
Рассматривается следующая дифференциальная краевая задача
|
|
l |
u f |
|
|
Lu f |
0 |
|
0 |
|
|
lg u fg |
||
|
|
|||
Где l0u f0 дифференциальная задача |
в области, а lg u fg условия на |
|||
границе области.
На примере одномерного линейного уравнения переноса:
Непосредственной проверкой можно пококазать, что точное решение уравнения переноса при заданной функции начального возмущения (x) и(t) 0, f (t, x) 0 будет следующим u(t, x) (x at) . Его можно использовать для проверки численных решений.
2. Сеточная область, сеточные функции и сеточные схемы (уравнения)
Для рассмотренной задачи введена равномерная сетка
|
p = 0, 1, …, P; |
m = 0, 1, …, M. |
||||||
В узлах сетки определена сеточная функция |
||||||||
|
p = 0, 1, …, P; |
m = 0, 1, …, M; |
||||||
uh Uh |
с нормой |
|
|
|
|
|
max(uh ) |
|
|
uh |
|
|
|
|
|||
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|||
где |
— компонента сеточной функции, относящаяся к узлу |
|
ПРОСТЫМИ |
для использования и анализа являются |
|
сетки |
|
|
.
равномерные
— постоянный шаг по времени, |
h — постоянный шаг по координате, |
||||||
Неравномерные сетки используются так же, |
например |
для решения |
|||||
уравнений с переменными коэффициентами или |
при |
наличии областей с |
|||||
резкими изменениями функций. |
На сетку можно |
спроектировать значения |
|||||
(составить таблицу) неизвестной функции u(x,t) : u(x ,t |
p |
) [u]p |
[u]h U |
h |
|||
|
|
m |
|
m |
|
||

34
На сеточных функциях может строится разностная задача
|
|
|
|
l huh |
f h |
|
Lhu |
h |
f |
h |
|||
h h |
h . |
|||||
|
|
0 |
0 |
|||
|
|
|
|
lg u |
fg |
|
|
|
|
|
|||
|
|
|
|
|
|
Причем, |
правя часть сеточной |
функцией |
пространства |
f h F |
(с |
||||||
|
|
|
|
|
|
|
|
|
|
h |
|
нормой |
|
|
|
|
|
), |
является элементом боле |
широкого |
пространства, |
поскольку |
|
|
f h |
|
|
|
|||||||
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
включает в себя не только значения правых частей сеточного уравнения, но и начально-краевых условий. Поэтому равномерная норма будет такой

 f h
f h 
 F max( f0h , fgh ) .
F max( f0h , fgh ) .
Одним из вариантов построения является замена дифференциальных величин конечно-разностными аналогами на сетке:
u (x, t) |
ump 1 ump |
, |
|
||
t |
|
|
|
|
u |
|
(x, t) |
ump 1 ump |
, |
u |
|
(x, t) |
ump ump 1 |
, |
u |
|
(x, t) |
ump 1 2ump ump 1 |
x |
x |
xx |
|
||||||||||
|
|
h |
|
|
h |
|
|
h2 |
|||||
Для рассмотренной дифференциальной задачи переноса одна из возможных
разностных задач имеет вид:
в области
p = 0, 1, …, P – 1; |
m = 0, 1, …, |
M – 1; |
m = 0, 1, …, M;
p = 1, 2, …, P, на границах.
Рассмотренная разностная схема при заданных m и p связывает значения функции в трех точках сетки, которые образуют конфигурацию, называемую шаблоном этой схемы. Тачки сетки при постоянном значении p=const образуют временной слой. Разностная схема представляет собой систему уравнений для значений сеточной функции и представляет собой сеточные уравнения, которые могут быть решены единственным образом или иметь множество решений, или не иметь решения вообще.
Вопрос единственности решения, как вопрос единственности дифференциальной задачи, требует особого исследования.
3. Погрешность метода
Введем в пространстве сеточных функций норму |
uh |
sup( uk |
) , |
|
|
|
U |
m |
|
|
|
m, p |
|
|
|
|
|
|
|
m = 0, 1, …, M; p = 0, 1, …, P.

35
Тогда погрешность (отклонение сеточной функции от точной таблицы
|
самой функции) выражается формулой |
uh [u]h |
|
|
|
. Если выполняется |
||
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|||
|
uh [u]h |
|
Chk , то говорят о точности порядка k. |
|||||
|
|
|||||||
|
|
|
U |
|||||
|
|
|
||||||
|
4. Аппроксимация. Невязка. |
|||||||
При подстановке в разностную задачу точного решения [u]h правая часть
не совпадет с правой частью схемы на невязку
|
f |
|
|
|
L uh L [u]h |
|
|
|
|
|
|
||||
|
|
|
F |
|
h |
h |
F |
|
|
|
|
|
|
||
Говорят, что разностная задача аппроксимирует дифференциальную с порядком k , если при уменьшении шага сетки невязка стремится к нулю и,
кроме того, |
|
|
C hk |
где C |
константа независящая от h. |
f |
|
||||
|
|
F |
1 |
1 |
|
|
|
|
|
|
Для рассмотренной выше разностной задачи соотношения, которые получены заменой производных по формулам численного дифференцирования в произвольном (p, m) узле, дают компоненту ошибки аппроксимации (невязку):
Представление о величине |
легко получить, если задать опорную |
точку и представить значения 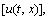 входящие в выражение для
входящие в выражение для 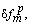 в виде разложения в ряды Тейлора относительно этой точки.
в виде разложения в ряды Тейлора относительно этой точки.
u(x h) u h ux 1 2 h2uxx 1
2 h2uxx 1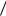 6 h3 uxxx 1
6 h3 uxxx 1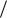 24h4 ux(4) 1
24h4 ux(4) 1 120h5ux(5) .. ,
120h5ux(5) .. ,
u(x ) u ut 1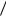 2 2utt 1
2 2utt 1 6 3 uttt .. .
6 3 uttt .. .
Тогда получим варианты аппроксимации производных
|
|
[u ] |
u(x h) u(x) |
|
h |
[u |
|
] |
h2 |
|
[u |
|
|
] .. uh O(h) , |
|
||||||||||||||
|
|
|
|
|
xx |
|
|
xxx |
|
||||||||||||||||||||
|
|
x |
h |
|
h |
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
[u ] |
u(x h) u(x h) |
|
h2 |
[u |
|
|
|
] .. uh O(h2 ) |
|
|
|||||||||||||||||
|
|
|
|
|
xxx |
|
|
||||||||||||||||||||||
|
|
|
x h |
|
2h |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[u |
] |
u(x h) 2u(x) u(x h) |
|
h2 |
|
[u |
|
|
|
|
] |
h4 |
[u |
|
] .. uh |
O(h2 ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
xx h |
|
|
h2 |
|
|
|
12 |
|
|
xxxx |
|
|
360 |
|
xxxxxx |
|
xx |
|
||||||||||
для невязки в опорной точке  получим:
получим:
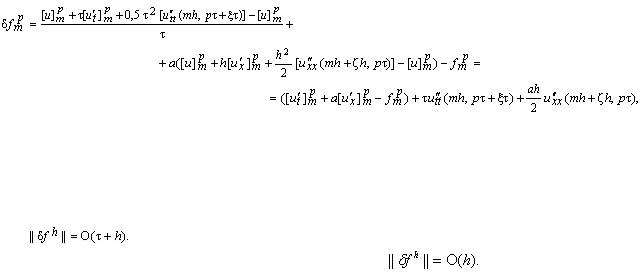
36
где 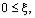
 Выражение в первых скобках в последнем равенстве равно нулю.
Выражение в первых скобках в последнем равенстве равно нулю.
Поскольку выкладки проводились для произвольного узла 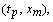 ,то получаем (в предположении ограниченности вторых производных
,то получаем (в предположении ограниченности вторых производных 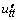 и
и 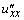 ):
):
Если и h имеют одинаковый порядок, то
5. Устойчивость и сходимость разностной задаче к дифференциальной.
Будем называть разностную схему устойчивой если: существуют h0 , 0 0
такие что для любых |
h h |
и любых |
возмущений |
h F |
таких что |
h |
|
0 |
, |
|
|
0 |
|
|
|
h |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
решение возмущенной |
разностной задачи |
L zh f h h отличается от решения |
||||||||
|
|
|
|
h |
|
|
|
|
|
|
не возмущенной задачи |
L uh f h |
не |
более |
чем |
само возмущение |
|||||
|
|
h |
|
|
|
|
|
|
|
|

 zh uh
zh uh 
 U C2
U C2 
 h
h 
 F .
F .
Теорема о сходимости разностной схемы к решению дифференциальной задачи. Если разностная схема аппроксимирует дифференциальную задачу с порядком точности k, и устойчива, то при уменьшении шага четки к нулю решение разностной задачи сходится к тачному и при чем точность.
|
uh [u]h |
|
C C hk . |
|
|
|
U |
1 |
2 |
|
|
|
|
|
Таким образом, для построенной разностной задачи необходимо проверить ее устойчивость и то, что она аппроксимирует дифференциальную задачу.
Откуда возникают возмущения в разностной схеме по отношению к дифференциальной. Это ошибки замены функций и их производных разностными аналогами, это ошибки округления при вычислениях и ошибки задания параметров исходной задачи.
Проблема аппроксимации дифференциальной задачи разностной решается достаточно просто с использованием Тейлоровских разложений. Полное же исследование устойчивости разностной схемы достаточно сложная задача, но есть один достаточно простой Необходимый спектральный
признак устойчивости по начальным возмущениям. Он заключается в требовании не нарастании возмущения во времени.
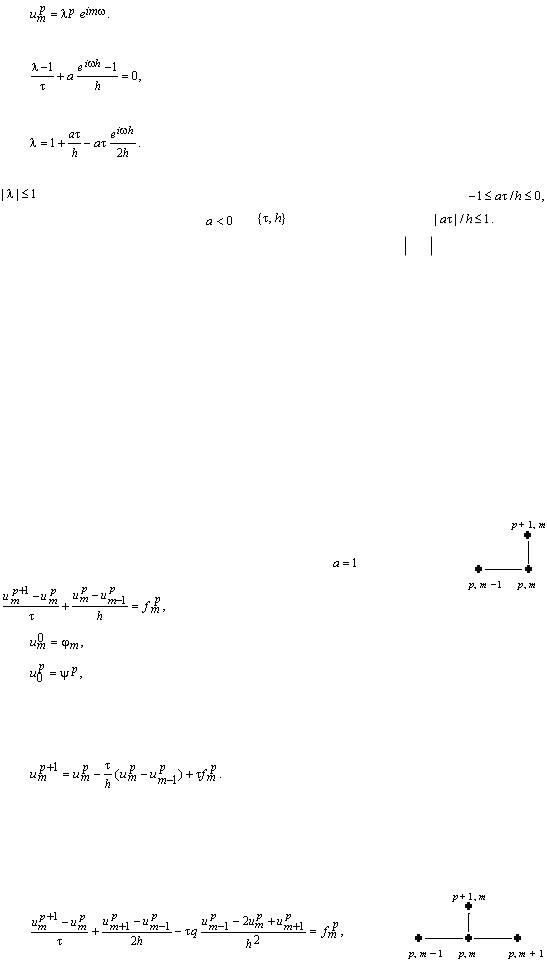
Для рассмотренной выше однородной разностной задачи ищем решение в виде
37
Подставляя его в разностные уравнения, получим
или
В силу произвольности отсюда получаем, что не нарастание решения
при всех будет |
тогда и |
только тогда, когда |
т. е. схема |
устойчива только, если в |
и |
выбраны так, что |
|
Последнее неравенство, записанное в форме h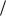 a , носит название условие Куранта.
a , носит название условие Куранта.
6. Наиболее употребительные разностные схемы для модельных уравнений переноса и диффузии.
Одной из проблем нахождения сеточного решения является решение сеточных уравнений, представляющих собой систему алгебраических (линейных или нелинейных) уравнений. Если схема позволяет явно записать решение на временном слое через решение на предыдущих слоях, то такие схемы называются явными. Обычно явные схемы не обладают хорошей устойчивостью. Неявные схемы обычно устойчивы, но приходится решать систему сеточных уравнений.
Явный левый уголок
Разностная схема (далее полагаем |
): |
|
p = 0, 1, …, P – 1; |
m = 1, …, |
M; |
m = 0, 1, …, M; |
|
|
p = 1, 2, …, P. |
|
|
Значение сеточной функции на |
верхнем временном |
слое p + 1 |
рассчитывается по ее значениям на нижнем слое p:
Порядок аппроксимации: О( + h).
Схема устойчива при 
Явная четырехточечная схема
Разностная схема:

|
38 |
p = 0, 1, …, P – 1; |
m = 1, 2, …, M – 1; |
где q — коэффициент искусственной (схемной) вязкости;
m = 0, 1, …, M;
p = 1, 2, …, P.
Значение сеточной функции на верхнем временном слое p + 1 при m = 1, 2, ..., M – 1 рассчитывается по ее значениям на нижнем слое p
Порядок аппроксимации (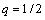 и
и 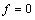 ):
):
Схема (при  ) устойчива при
) устойчива при 
Явная центральная трехточечная схема
Разностная схема:
p = 0, 1, …, P – 1; |
m = 1, 2, …, |
M – 1; |
|
m = 0, 1, …, M; |
|
u0p uMp p |
p = 1, 2, …, P. |
|
Значение сеточной функции на верхнем временном слое p + 1 находится по ее значениям на нижнем слое р (значения сеточной функции в граничных точках xm=0, M рассчитываются по схеме «явный левый/правый уголок»):
Порядок аппроксимации:
Схема устойчива при 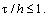
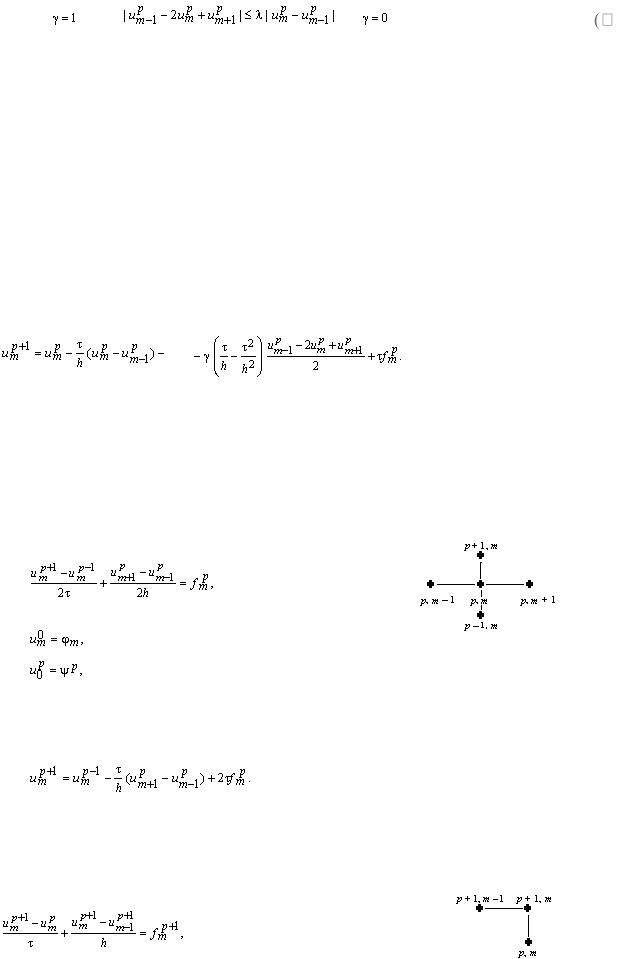
Гибридная схема (схема Федоренко)
Разностная схема:
p = 0, 1, …, P – 1; |
m = 1, 2, …, M – 1; |
|
m = 0, 1, …, M; |
u0p uMp p |
p = 1, 2, …, P. |
|
|
39 |
|
|
Здесь |
при |
и |
в противном случае |
— |
численно подбираемый параметр гибридной схемы). |
|
|||
|
Гибридные схемы |
используются при |
расчетах процессов, имеющих |
|
особенности разрывного характера (или большие градиенты искомых функций). Вблизи областей с большими градиентами искомого решения используется схема первого порядка аппроксимации, обладающая сглаживающими свойствами (см., например, поведение численного решения, полученного по схеме «явный левый уголок» при начальном условии третьего типа). В «гладких» областях расчет ведется по немонотонной схеме второго порядка аппроксимации (см., например, поведение численного решения,
полученного по явной четырехточечной схеме при том же начальном условии). Значение сеточной функции на верхнем временном слое p + 1
рассчитывается по ее значениям на нижнем слое p:
Порядок аппроксимации: Аналитические и численные методы решения уравнений математической физики Аналитические и численные методы решения уравнений математической физики O( h) .
Схема устойчива при 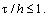
Схема «Чехарда»
Разностная схема:
p = 1, …, P – 1; |
m = 1, 2, …, M – 1; |
|
m = 0, 1, …, M; |
p = 1, 2, …, P.
Алгоритм численного решения задачи: значения сеточной функции на верхнем временном слое p + 1 рассчитываются по ее значениям на двух нижних слоях:
Порядок аппроксимации: 
Схема устойчива при 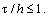
Неявный левый уголок (Схема бегущего счета – на право)
Разностная схема:
p = 0, |
…, |
P – |

40
1; m = 1, …, M;
m = 0, 1, …, M;
p = 1, 2, …, P.
Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям в точках верхнего и нижнего p временных слоев:
Порядок аппроксимации: O( h) .
h.
Неявный правый уголок (Схема бегущего счета – на лево)
Разностная схема:
p = 0, …, P – 1; m = 0, …, M – 1; m = 0, 1, …, M;
p = 1, 2, …, P.
Значение сеточной функции на верхнем временном слое p + 1 рассчитывается по ее значениям в двух точках верхнего и нижнего p-слоев:
Порядок аппроксимации: O( h) . Схема устойчива при 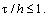
Неявная четырехточечная схема
Разностная схема:
p = 0, 1, …, P – 1; |
m = 1, 2, …, M – 1; |
|
m = 0, 1, …, M; |
p = 1, 2, …, P.
Алгоритм численного решения полученной системы линейных уравнений с матрицей трехдиагональной структуры — метод прогонки.
Для предложенного метода рассматриваются пять типов условий на правой границе области интегрирования:
1)схема «явный левый уголок»;
2)схема «неявный левый уголок»;
3)схема «неявный правый уголок»;
