Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

8337

.pdf

Скачиваний:

Добавлен:

24.11.2023

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

§ 1.4. Задача Штурма-Лиувиля

Другим поставщиком ортогональных систем функций, да еще полных в

H 2 [a, b] и с некоторыми заданными свойствами, является решение задачи

Штурма-Лиувиля.

Линейным оператором А в пространстве Н называется набор действий,

отображающих функцию		u(x) H в функцию		f (x) H . Это обозначается		Au f ,
в силу	линейности,	для любых		функций	u1 (x),u1 (x) H	имеем:
A( 1u1 2u2 ) 1 Au1 2 Au2 . Оператор А может быть :
- Положительно определенным			(Au,u) 0 , или неотрицательным
(Au,u) 0 u H ,
- Самосопряженным при (Au,v) (u, Av) u,v H
Функция u H и		удовлетворяющая		уравнению	Au u , называется
	ˆ				ˆ ˆ
собственной	функцией	линейного	оператора, а соответствующее			число

R собственным числом.

Верна теорема 1:

Если оператор А в пространстве Н неотрицателен (неположителен) и самосопряжен, то все его собственные функции взаимно ортогональны, а соответствующие собственные числа неотрицательны (неположительны).

Рассмотрим

одномерный

ограниченный

отрезок

x [a,b] R

функциональное

пространство

u(x) H2 [a, b] .

Рассмотрим так

же

самосопряженный дифференциальный оператор 2-го порядка

1 d

здесь u(x) C2 [a, b] дважды непрерывно-дифференцируемая функция,

(x) C [a, b] ,

(x) 0непрерывная и положительная функция (вес в H 2 [a, b]),

p(x) C1 [a, b] ,

p(x) 0 ,

q(x) C [a, b] , q(x) 0 .

Задача Штурма-Лиувиля (S-L) состоит в следующем: определить все

собственные

числа

оператора

соответствующие

им собственные

функции uˆ (x) , удовлетворяющие граничным условиям на границах области

[a,b].

	1 d		du	qu u ,
Au		p

	dx		dx

u(a) u'				(a) 0	.
a(u)	1	1	x		.
		u(b)	u'	(b) 0
	2	2	x

Здесь i , i параметры граничных условий в граничном операторе a(u)

i2 i2 0, i i 0 . Различаются 3 типа:

i 0 , u(a) u(b) 0 - граничное условие 1-го рода (Дирихле),

i 0 , ux' (a) ux' (b) 0 - граничное условие 2-го рода (Неймана),

i 0,

i 0

- граничное условие 3-го рода (смешанное).

Проблема состоит в том, что линейное дифференциальное уравнение имеет, как известно единственное решение при условии в одной точке (начальная задача Коши), а в разных точках на границах области решения – это краевая задача, которая может как не иметь решений, так и иметь множества решений.

Теорема 2 (Стеклова) о решении задачи S-L и его свойствах.

При сделанных предположениях о коэффициентах уравнения S-L справедливо следующее:

- Имеется счетное множество различных собственных чисел 1, 2 , 3 ,..., n ,... и соответствующих им различных собственных функций uˆ1,uˆ2 ,uˆ3 ,...,uˆn ,... задачи S-L. - Все собственные числа не положительны и монотонно нарастают по модулю

i 0			1	2	3	...		n	...
i 0			1	2	3	...		n	...
- Возможно	1	0 только при q(x) 0					, но тогда u1 const
									ˆ

- Собственные функции задачи S-L соответствующие различным собственным

числам образуют полную, ортогональную систему функций в пространстве

H 2 [a, b].

Т.е. Любая функция, удовлетворяющая граничным условиям задачи, в

нем может быть разложена в ряд Фурье по ортогональной системе собственных

функций, который абсолютно и равномерно сходится к этой функции.

		(u,uˆi )
u(x) ciuˆi ,	ci	(u,uˆi )
			uˆi	2
				2
i 1

Несколько важных примеров задач S-L

1) Рассмотрим тригонометрический оператор A(u)

d 2u

u(x) H

1[0, l]

Задача S-L имеет вид:

d 2u

u ,

(x) 1 0 , p(x) 1 0 ,

q(x) 0 0

dx2

Общее решение u(x) C1 sin x C2 cos x

2) Рассмотрим оператор Чебышева A(u)

1 x

u(x) H ( 1, 1)

Задача S-L имеет вид: Au u ,

(x)

0 ,

p(x)

1 x2

0 ,

q(x) 0 0 , или

(1 x2 )u'' xu' u

- уравнение Чебышева

Сделав замену переменной x cos t , уравнение будет следующим:

u'' u 0 , которое при

будет u''

n2u 0

Общее решение

которого u(t) C1 sin nt C2 cos nt ,

в переменной

х будет

функция Чебышева:

un (x) C1 sin(n arccos x) C2 cos(n arccos x) .

Если задать граничное условие u(1) 1 ,

то решениями уравнения будут

многочлены Чебышева T(x) , и как собственные функции задачи S-L, они

представляют собой полную ортогональную систему в

H2 ( 1, 1)

3) Рассмотрим оператор Лежандра

A(u)

(1 x

)

, u(x) H

( 1, 1)

Задача S-L имеет вид: Au u ,

(x) 1 0 ,

p(x) 1 x2

0 , q(x) 0 0 , или

(1 x2 )u' ' 2xu' u

- уравнение Лежандра,

При n n(n 1) его частными решениями будут многочлены Лежандра 1-рода.

Другим частным решением будут функции Лежандра 2-рода является:

Qn (x) Pn (x)

(1 x2 )P2 (x)

тогда общее решение уравнения Лежандра будет un (x) C1 Pn (x) C2

Qn (x) .

Некоторые первые из

Q (x) будут такими: Q (x)

1 x

, Q (x)

1 x

Q (x)

3x2 1

1 x

x ,

Q (x)

5x2 3x

1 x

1 x 2

Система функций Pn (x) также как и Qn (x) полна и ортогональна в H2 ( 1, 1) .

1 d

4) Рассмотрим оператор Бесселя

A(u)

u ,

u(x) H2 (0, l)

x dx

Задача S-L имеет вид: Au u ,

(x) x 0,

p(x) x 0 ,

q(x)

0 , или

x2u' ' xu' p2u x2u ,

а при

x2u' ' xu' (x2 2 p2 )u 0

- уравнение Бесселя c параметром .

Заменив переменную t x получим

t2 u'

' t u'

(t2

p2 ) u 0

уравнение Бесселя без параметра, его частными решениями будут функции Бесселя порядка p.


Находя их решение в виде степенного ряда up (t) t antn	при p
n 0
с p 0

		( 1)n (t / 2)2n p
	u p (t)
	u p (t)	n ( p n 1)
	n 0	n ( p n 1)

		( 1)n (t / 2)	2n p
J p (t) ,	u p (t)			J p (t)

	n 0	n ( p n 1)


где ( p) y p 1e y dy - гамма функция Эйлера
0
при p 0 , ( p 1) p ( p) , для целых p k 0				(k) 12...k 1 (k 1)!,
а при p 0 определим ( p)			( p k 1)	где p ( k 1, k), для

			p( p 1)..( p k)
1		0
целых p k 0 ,
целых p k 0 ,	( k )

Полученные функции Бесселя 1-го рода

J p (t)

, J p (t)

, линейно

независимы

при

нецелых

знаниях

p 0

значит

составляют

фундаментальный

базис

решения

уравнения

Бесселя

up (t) C1J p (t) C2 J p (t) .

Если же p 0,1, 2,..k,.. целые, то эти функции

линейно

зависимы

J k (t) ( 1)k Jk (t)

фундаментального

базиса не

составляют. Функции Бесселя имею ряд свойств

(0) 1

(0) 0

(0)

(t) 0

. Справедливы

рекуррентные соотношения

J p 1 (t)

2 p

J p (t) J p 1 (t) ,

J p'

(t) 0.5[J p 1(t) J p 1(t)] .

Для полуцелых функций Бесселя

из ряда для J

0.5 (t) можно

получить

J 0.5 (t)

sin(t) , J 0.5 (t)

cos(t) ,

J 1.5 (t)

(

sin(t)

cos t) , ..

Для построения фундаментального базиса для решения уравнения Бесселя при целых вводится функция Бесселя 2-го рода называемая функцией

Немана:
N p (t)	J p (t) cos( p) J p (t)	для нецелых p	и Nk (t) limN p (t) для целых p .
N p (t)	sin( p)	для нецелых p	и Nk (t) limN p (t) для целых p .
	sin( p)		p k

При нецелых p функция Неймана является решение уравнения Бесселя как комбинация его независимых решений, а целых p она также в пределе является решением. Функции J p (t), N p (t) линейно независимы так как J p (0) 0, N p (0) . Поэтому общее решение уравнения Бесселя можно записать при любом p

в следующем виде: up (t) C1 J p (t) C2 N p (t) , up (x) C1J p ( x) C2 N p ( x) .

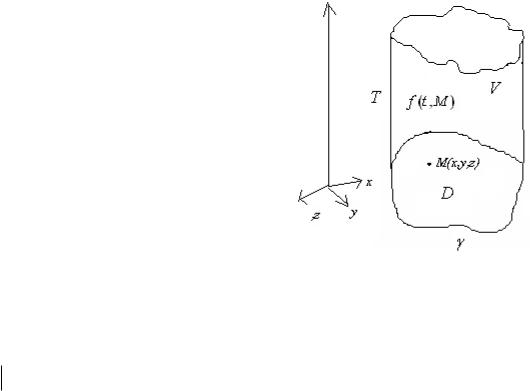
Функции Бесселя являются полной системой функций в u(x) H2 (0, l) очень

часто используются для решения задач Математической физики, поэтому их графики приводим ниже:

II. Численные методы решения уравнений математической физики

§ 2.1 Проекционные методы решение стационарных задач

Пусть физика на основе своих законов (законы сохранения вещества, импульса или энергии и прочих связей действующих в физической системе

сформулирована	математическая задача для координаты	u(x,t) в
цилиндрической области (границы неподвижны):
Lu f , x V ;	V D T
l(u) , x	T

Lu - линейный дифференц. оператор в V

f - правая часть

l(u) - линейный оператор граничных усл. на

- правая часть

Рассматриваем

функциональное

пространство, H 2 (D) в котором будем искать решение. Выделим в нем

подпространство функций, удовлетворяющих граничным условиям:

F(D) {u(x) l(u) , x } H2 (D) . Построить такое подпространство

сложно, но можно например через базис собственных функций задачи S-L. Для любой функции u(t, x) F(D) может быть вычислена невязка

(u) L(u) f

Метод Галеркина (Бубнова-Галеркина)

Самым простым и понятным методом приближенного решения уравнения

Lu f является проекционный метод Галеркина. Его идея минимизации невязки состоит в том, что невязка должна быть ортогональна подпространству F(D) . Действительно, пусть определен полный бесконечный базис { 1 (x), 1 (x),..., n (x),..} F (D) , тогда условие минимальности невязки, есть условие ее ортогональности ко всем r (x) , т.е. ( n , r ) 0 . Как и в рядах Фурье рассмотрим конечную линейную оболочку

un (x) k k (x) 1 1 (x) 2 2 (x) ... n n (x) F(D)

k 1

n	n
(un ) L(un ) f L( k k (x)) f	k L k (x) f
k 1	k 1
n
( (un ), r )) 0 k (L k , r ) ( f , r ) 0;		r 1,.., n .

k 1

Получена система линейных алгебраических уравнений относительно k

B (L k , r ),

C ( f , r ),

( k )

B C .

Решив эту систему (методами Крамера, Гаусса, обратной матрицы) мы найдем наилучшее приближение в базисе размерности n , а в силу полноты бесконечной базисной системы это решение будет приближаться решению задачи.

	n
u (x)				(x) u(x)	.
n		k	k	n	.
	k 1

Пример 1: Lu u'' u x,

u(0) u(l) 0 .

Выберем базис

(x) sin x,

Тогда L k (x) k2 sin k x sin k x (1 k2 ) sin k x ,

k r

Brk ( r , L k ) sin r x (1 k2 ) sin k xdx

(1 k2 )

kr ;

где kr

k r

( , f )

x sin xdx

cos l .

Матрица В диагональная и поэтому система решается тривиально:

	l cos r l		: (1 2 )	l2	2 cos k
			: (1 2 )		l(1 2 )
k		r	k	2	l(1 2 )
		r			k

	Lu a (x)u'' a (x)u'			a (x)u f (x),
Пример2:	2	1		0
Пример2:	u u(x). x ( 1,		1),		u( 1)	A, u( 1)	B.

Перейдем к задаче с нулевыми краевыми условиями при помощи замены

u(x) v(x) A 0.5(B A)(x 1) x ( 1, 1)

L(u) L(v) 0.5a1 (B A) 0.5(B A)(x 1) f (x)

L(v) f (x); v( 1) 0, v( 1) 0;

f (x) f (x) 0.5a1 (B A) 0.5a0 (B A)(x 1)

Ищем решение методом Галеркина в базисе k (x 1)(x 1)k ,

удовлетворяющем нулевым условиям (но не ортогональном), до двух членов:

v(x) 1 1 2 2

Учитывая, что k			(x 1)(x 1)k		(x 1)k 1 2(x 1)k и [(x 1)n ]' n(x 1)n 1
		(x) (x 1)2 2(x 1);					2	(x) (x 1)3 2(x 1)2	;
		1					2
			'	(x) 2(x 1) 2; '		(x) 3(x 1)2 4(x 1) ;
			1		2
				'' (x) 2; '' (x) 6(x 1) 4;
				1	2
L( ) a [2] a [2(x 1) 2] a [(x 1)2 2(x 1)];
1		2		1	0
L(	2	) a [6(x		1) 4] a [3(x 1)2 4(x 1)] a [(x 1)3					2(x 1)2 ]
	2	2		1				0

Далее, вычислим матрицу Галеркина Brk ( r , L k ) r L k dx

и вектор правой части Cr ( r , f ) f r dx

																																	29
											1													1
B		( , L )											L dx													[(x 1)2				2(x 1)] {[2] a [2(x 1) 2] a [(x 1)2 2(x 1)]}dx
11			1			1									1				1															1					0

											1													1
											1														1
B		( , L					)							L						dx							[(x 1)2				2(x 1)] {[6(x 1) 4] a [3(x 1)2 4(x 1)] a [(x 1)3 2( x 1)2											]}dx
12			1			2									1				2																		1				0

											1														1
												1													1
B		(			, L			)									2	L		2	dx							[(x 1)3			2(x 1)2 ] {[6(x 1) 4] a [3(x 1)2										4(x 1)] a [(x 1)3 2(x 1)2		]}dx
22			2			2											2			2																		1			0

												1													1
											1														1
B		(			, L )											2		L dx									[(x 1)3 2(x 1)2 ] {[2] a [2(x 1) 2] a [(x 1)2 2(x 1)]}dx
21			2			1										2			1															1						0

									1		1									1					1
C ( , f )										f dx												[(x 1)2							2(x 1)] { f (x) 0.5a (B A) 0.5(B A)(x 1)}dx
1			1									1																						1

									1											1
									1												1
C	2	(		, f )									2		f dx								[(x 1)3 2(x 1)									] { f (x) 0.5a (B A) 0.5(B A)(x 1)}dx
	2		2										2																					1

									1												1
			Все эти интегралы необходимо вычислить (до числа) численно или
аналитически с учетом вида коэффициентов																																				a1 (x), a2 (x) и возможной замены
переменной интегрирования t x 1,
																														1				(x 1)		n 1	1		2	n 1
			При этом как известно																												(x 1)n dx			(x 1)					2		.
																														1				n 1			1		n 1
																														1							1
			Вычислим при a1 1, a2 1, A 0, B 0, f (x) x -- достаточно простой случай
Тогда для неизвестных коэффициентов Галеркина получим линейную систему
уравнений
1						0.2 47.2													1.6							1				0.2					1				0.2
																												2				ее решение
2				10.8								7.1							13									2		10.8					2			10.8
																															1.2
																															1
																															0.8
																															0.6										Ряд1
																															0.4
																															0.2
																															0
																			-1.5							-1			-0.5			0	0.5	1			1.5
			Метод наименьших квадратов

Идея метода наименьших квадратов используется в многочисленные приложения математики, и в частности, для решения краевых задач. Она состоит в минимизации квадратичной невязки (квадратичного уклонения) по неизвестным коэффициентам разложения по базису.

	n	n
Так как n L(un ) f	L( k k (x)) f	k L k (x) f , то подберем
	k 1	k 1

коэффициенты k таким, чтобы квадрат невязки n2 был минимален, для этого необходимо что бы:

n2	0 , при этом	2	n
ak	0 , при этом	n	2 k	L k (x) f L r	(x) 0	или B C
		ar	k 1
		ar	k 1
где	B (L k , L r ), C		( f , L r ), ( k ) .
	Метод Ритца
	Если в краевой		задаче	Lu Au положительный самосопряженный

оператор, то задача нахождения его решения u(x) F(D) эквивалентна нахождению минимума функционала J (u) (Au,u) 2(u, f ) .

J		n	n			n
J		L k k (x), j j		(x)	2 j j (x) f		0 или B C ?
a j		L k k (x), j j		(x)	2 j j (x) f		0 или B C ?

		k 1	j 1			j 1
	B (L k , r ),		C ( f , r ),			( k )	B C .

Что совпадает с методом Галеркина, однако метод не требует постановки

дифференциальной краевой задачи, а позволяет решать вариационную краевую

задачу.

Метод конечных элементов

Для решения стационарной задачи одним из приведенных выше методов используется система независимых (желательно ортогональных) функций, удовлетворяющих краевым условиям. Тогда приближенное решение задачи ищется в линейной оболочке этой системы базисных функций. В Методе конечных элементов (МКЭ) используется специальная система базисных функций с конечным носителем. Для ее построения область D переменных задачи разбивается на элементы d j [x j 1 x x j 1 ] , в каждом из которых

определении функция j (x) (например, непрерывная кусочно-линейная)

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.11.20231.55 Mб08332.pdf
#
24.11.20231.55 Mб08333.pdf
#
24.11.20231.55 Mб08334.pdf
#
24.11.20231.55 Mб08335.pdf
#
24.11.20231.55 Mб08336.pdf
#
24.11.20231.55 Mб08337.pdf
#
24.11.20231.55 Mб08338.pdf
#
24.11.20231.56 Mб08339.pdf
#
21.11.2023155.13 Кб0834.pdf
#
24.11.20231.56 Mб08340.pdf
#
24.11.20231.56 Mб08341.pdf