
6858
.pdf
30
|
|
|
2 |
|
ml2 |
l |
2 |
|
ml2 |
|
ml2 |
|
ml |
2 |
|
|
|
Jz = JzC + md |
|
= |
|
+ m |
|
|
= |
|
+ |
|
= |
|
|
. |
|
|
|
12 |
|
12 |
4 |
3 |
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
Ответ: |
J = ml2 |
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема 6. Теорема об изменении кинетического момента
6.1. КИНЕТИЧЕСКИЙ МОМЕНТ
Теоремы о движении центра масс и об изменении количества движения описывают только поступательную часть движения твердого тела. Вращательную часть движения описывает теорема об изменении кинетического момента.
Введем понятия:момент количества движения и кинетический момент.
R |
R |
R |
R |
R |
относительно точки О. |
Величину mO (F ) = r |
× F |
называют моментом силыF |
|||
Момент количества движения относительно некоторой точки определяется аналогично, но вместо вектора силы берется вектор количества движения.
То есть:
моментом количества движения материальной точки относительно некоторого центра называется векторное произведение
R |
R R |
R |
|
mO (mv ) = r |
× mv. |
(6.1) |
|
|
|
|
|
а проекция этого вектора на некоторую ось z называется моментом количества
движения материальной точки относительно этой оси ( R ) mz mv .
31
|
R |
R |
|
||
|
mO (mv ) |
|
|||
|
|
z |
|
|
R |
|
|
|
|||
|
|
|
|
|
mv |
|
|
R |
|
|
|
|
|
mv |
|
|
|
|
|
R |
|
|
|
O |
h |
r |
|
|
h |
|
|||||
|
|
|
|||
|
π 2 |
R |
|||
π |
2 |
(mv ) x y |
|||
Oxy |
|
||||
|
|
|
|||
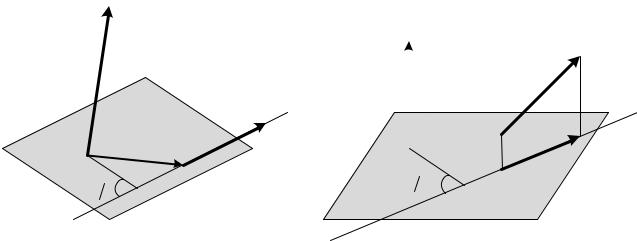
Рис. 6.1. |
Рис. 6.2. |
Направление вектора кинетического момента количества движения относительно точки определяется по правилу правого винта.
Его модуль равен произведению количества движения на плечо (рис. 6.1):
( R) = ×
mO mv mv h,
где h – плечо вектора количества движения относительно точки О.
O ( |
R |
) |
|
кг× м2 |
|
Размерность модуля момента количества движения: m |
mv |
|
= |
|
. |
|
|
|
|
с |
|
Чтобы вычислить момент количества движения относительно оси надо :
Спроектировать вектор на плоскость перпендикулярную оси; Модуль этой проекции (рис. 6.2) умножить на ее плечо относительно точки пересечения оси с плоскостью; Добавить знак в зависимости от направления вектора.
В результате получим:
R |
× h, |
mz (mv ) = ± (mv )xy |
(6.2)
Теперь введем понятие кинетического момента.
Кинетическим моментом механической системы относительно некоторого центра О (или оси) называется сумма моментов количеств движения всех точек данной системы относительного данного центра (или оси):
R |
n |
R |
R |
n |
R |
× mi |
R |
, |
KO |
= ∑ mO (m i |
v i ) = ∑ ri |
vi |
|||||
|
i=1 |
|
|
i=1 |
|
|
|
(6.3) |
|
|
|
|
|
|
|
|
|

32
n |
R |
|
|
|
|
Kz = ∑ mz (m i v i ). |
|
|
i=1 |
|
(6.4) |
|
|
|
Если точка О является началом системы координат, то спроектировав кинетический моментотносительно центра О на оси, получим кинетические моменты относительно координатных осей:
|
R |
n |
R |
Kx |
= (KO )x |
= ∑mx (m i v i ) |
|
|
|
i=1 |
|
|
R |
n |
R |
Ky |
= (KO ) |
= ∑my (m i v i ) |
|
|
y |
i=1 |
|
|
|
||
|
R |
n |
R |
Kz |
= (KO ) |
= ∑mz (m i v i ) |
|
|
z |
i=1 |
|
|
|
||
|
|
|
(6.5) |
Примечание
Если механическая система представляет собой твердое тело, то кинетические моменты должны определяться не суммированием, а путем интегрирования по объему.
6.2. КИНЕТИЧЕСКИЙ МОМЕНТ ВРАЩАЮЩЕГОСЯ ТЕЛА |
, |
||
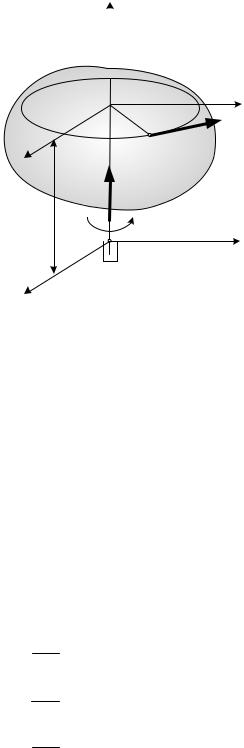
Пусть материальное тело вращается относительно оси z с угловой скоростью |
|||
(рис. 6.3). Вычислим кинетический момент тела относительно оси вращения |
|||
- . |
|
|
|
Для этого выделим бесконечно малый элемент объема с массой , который |
|
||
находится от оси вращения на расстоянии . |
. Его скорость будет |
|
|
равна ,, а его кинетический момент определится по формуле: |
|
||
dK z = dm × vh = dm ×ω h2 =ω ( x2 + y 2 ) dm. |
|
||
Кинетический момент всего тела получим, проинтегрировав моменты коли- |
|
||
честв всех бесконечно малых объемов тела: |
|
||
K z = ∫ d K z = ω ∫ ( x2 + y 2 ) dm. |
|
||
V |
V |
|
|
где интеграл |
|
|
|
∫( x2 + y2 ) dm = J z
V
представляет собой осевой момент инерции .
33
Таким образом, кинетический момент вращающегося тела относительно оси вращения равен произведению осевого момента инерции на угловую скорость:
Kz = Jz ω. |
(6.6) |
||||
|
z |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
h |
R |
|
d mv |
x′
ωR
z |
y |
x
Рис. 6.3.
6.3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА
ТЕОРЕМА
Производная по времени от кинетического момента механической системы относительного некоторого центра (или оси) равна главному моменту внешних сил относительно этого же центра (или оси):
dK |
O |
n |
R |
R |
|
|
|||
|
= ∑mO (Fke ) |
|||
|
|
|||
dt k =1 |
|
(6.7) |
||
или
dKx
dt
dK y
dt
dKz
dt
n |
R |
|
= ∑mx (Fke ) |
|
|
k =1 |
|
|
n |
R |
|
= ∑my (Fke ) |
|
|
k =1 |
|
|
n |
R |
|
= ∑mz (Fke ) |
|
|
k =1 |
. |
(6.8) |
Доказательство
Рассмотрим сначала одну материальную точку.
34
Запишем для нее основное уравнение динамики:
|
|
|
|
|
|
|
|
|
|
R |
= F . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
m a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Помножим радиус-вектор точки на левую и правую части равенства: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
× m a |
= r × F . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
R |
R |
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В правой части r × F |
= M O |
( F ) по определению, а в левой части |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
R |
|
d |
( |
R |
) |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
R |
|
R R |
|
|
dv |
R |
mv |
|
d |
( |
R |
|
R |
) |
|
dr |
R |
|
d |
|
R |
|
R |
R |
R |
|||||
r × m a |
= r |
× m |
= r × |
|
|
= |
r |
× mv |
− |
× mv |
= |
|
m |
mv |
− v |
× mv. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
dt |
|
|
dt |
|
|
|
|
dt |
|
dt |
|
O ( |
|
) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
|
R |
= 0 |
и мы получаем равенство |
||||
Вектор v |
|
параллелен векторуmv |
поэтому v × mv |
||||||||||||||||||||||||||||
|
d |
|
O |
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
R |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m |
|
mv |
|
= r × m a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dt
Для материальной точки теорема доказана.
Рассмотрим теперь механическую систему.
Просуммируем полученные равенства для всех точек системы.
В левой части получим:
n |
d |
|
R |
R |
|
|
∑ |
|
m |
(m v ) |
= |
||
|
||||||
dt |
|
O |
k k |
|
|
|
k =1 |
|
|
|
|
|
|
d |
n |
R |
R |
|
|
dK |
O |
|
|
m |
(m v ) |
= |
|
. |
|||
|
|
|
||||||
|
∑ |
O |
k k |
|
|
dt |
||
dt k =1 |
|
|
|
|
||||
В правой части отделим моменты внешних сил от моментов внутренних сил:
n |
R |
R |
n |
R |
R |
n |
R |
R |
|
|
|
|
|
|
|||
∑ mO (Fk ) = ∑ mO (F ek ) + ∑ mO (F ik ). |
||||||||
k =1 |
|
|
k =1 |
|
|
k =1 |
|
|
Внутренние силы, как силы взаимодействия, попарно равны и противоположно направлены, и по этой причине
∑ R ( i ) =
n R
mO F k 0.
k=1
Врезультате получим равенство:
dKO |
= n |
O ( |
R |
k ) |
|
|
|||||
|
∑ |
|
|||
dt |
|
R |
|
e |
. |
|
m |
F |
|||
|
|
|
|||
k =1
Теорема доказана.
35
Вывод из теоремы:
внутренние силы не могут изменить кинетический момент механической системы.
6.4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Предположим, что материальное тело вращается относительно оси z . По формуле (6.6) его кинетический момент будет равен Kz = Jzω и тогда в соответствии с теоремой об изменении кинетического момента
d [ J zω ] |
= n |
|
z ( |
|
k ) |
|
|
|
R |
||||
dt |
∑ |
|
|
|||
|
m |
|
F |
e |
. |
|
|
|
|
|
|||
k =1
Если тело в процессе вращения не изменяется, то Jz = const и мы получаем дифференциальное уравнение вращательного движения твердого тела:
J |
|
|
dω |
= |
|
n |
|
|
R |
|
||
|
|
|
|
|
|
|
||||||
|
z |
|
|
dt |
∑ mz |
(F ek ) , |
(6.9) |
|||||
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
Если учесть, что ε = |
dω |
= |
d 2ϕ |
, |
уравнение (6.9) можно записать в виде |
|
||||||
|
|
|
||||||||||
|
|
|
|
dt |
|
dt 2 |
|
|
|
|
||
Jz |
ε = Jzϕ = |
|
n |
e |
|
|||||||
|
|
|
|
|
|
|
&& |
∑ mz (F k ) |
(6.10) |
|||
|
|
|
|
|
|
|
|
|
||||
k =1
Из сравнения формулы (3.8) для поступательного движения и формулы (6.10) для вращательного движения видно, что при поступательном движении мерой инертности тела является его масса, а при вращательном − его момент инерции.
6.5. СЛУЧАИ СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА
Из теоремы об изменении кинетического момента следуют два положения.
Следствие 1
Если главный момент внешних сил механической системы относительно некоторого центра все время равен нулю, то кинетический момент системы относительно этого центра остается неизменным.
|
|
|
|
dK |
|
|
R |
n |
R |
R |
|
O |
|
и KO = const. |
|
Действительно, если ∑ mO (F ek ) ≡ 0, |
то |
|
= 0 |
||||
|
|
||||||
k =1 |
|
|
|
dt |
|
||
Следствие 2
36
Если главный момент внешних сил относительно какой-либо оси все время равен нулю, то кинетический момент системы относительно этой оси остается неизменным.
n |
R |
|
|
dK z |
|
|
|
|
= const. |
|
|
|
|
|||
Действительно, если ∑ mz (F ek ) |
≡ 0 то |
= 0 |
и Kz |
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
k =1 |
|
|
|
|
|
dt |
, |
|
|
|
|
|
|
|||
номерно-. ! , /012 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
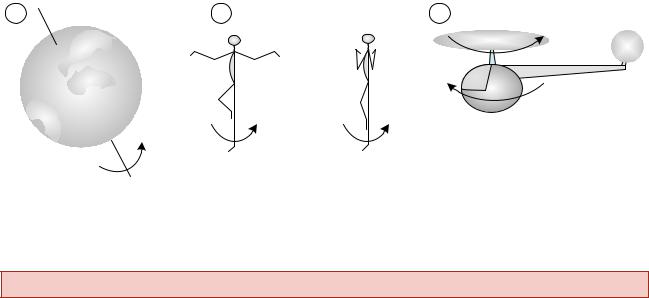
1. Если механическая система представляет собой одно неизменяемое твердое |
||||||||||||||||
тело, то |
|
|
|
и поэтому |
|
|
, то есть тело вращается рав- |
|||||||||
2. Если система изменяема, то из |
|
|
|
|
следует, что увеличение мо- |
|||||||||||
|
|
уменьшение угловой скорости (и наоборот). |
||||||||||||||
мента инерции вызывает |
|
! , /012 |
|
! , ! , |
|
|
|
|||||||||
вательно, вращение - |
|
/012 |
|
|
|
|
|
|
|
|||||||
3. Если система состоит из двух (или нескольких) вращающихся тел с одной |
||||||||||||||||
осью вращения, то из |
|
|
|
|
|
следует, что |
|
|
|
, и, следо- |
||||||
одного тела будет вызывать вращение второго тела с |
||||||||||||||||
угловой скоростью, |
!! , . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
J z = const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|
J zω z = const |
|
|
|
ω 2 |
|
|
|
|
||||
|
|
|
|
J1 > J2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
ω1 < ω2 |
|
|
|
|
|
|
|
|
||||
ω z = const |
|
ω1 |
|
|
|
ω 2 |
|
J1ω1 + J2ω2 |
= const |
|
||||||
|
|
|
|
|
J1ω1 = −J2ω2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 6.4
Тема 7. Мощность и работа сил
7.1. ОПРЕДЕЛЕНИЕ МОЩНОСТИ И РАБОТЫ СИЛЫ
Мощностью силы называется величина, равная скалярному произведению силы на скорость точки ее приложения:
R |
R |
R |
R |
N = F |
×v |
= F v cos (F , v ). |
|
|
|
|
(7.1) |
Мощность может быть как положительной, так и отрицательной (рис. 7.1 ).

37
F |
F |
|
|
|
F |
|
|
|
|
|
|
||||
α |
R |
|
α |
|
|
α |
R |
|
|
|
R |
|
|
||
|
|
|
|
|
|||
cosα > 0 |
v |
cosα < 0 |
|
cosα = 0 |
v |
||
v |
|
||||||
N > 0 |
|
|
N < 0 |
|
|
N = 0 |
|
Рис. 7.1
Размерность мощности [N ] = [F ][v] = Н × м/ с = Вт.
Работой силы за некоторый промежуток времени Dt = t - t0 называется величина, равная интегралу от мощности силы по времени:
|
t |
|
|
|
dA |
|
|
|
A = ∫ N dt , и следовательно N = |
|
(7.2) |
||||||
dt |
||||||||
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
Если мощность постоянна, то A = N |
t . |
|
||||||
|
[ A] = [N ][t] = Вт× с = |
Н × м× с |
= Н × м |
|
||||
Размерность работы |
|
. |
||||||
|
|
с |
||||||
Выражение под знаком интеграла в (7.4) есть работа за бесконечно малый про- |
||
межуток времени,которую называютэлементарной работой: |
|
|
|
∙ 6 |
(7.3) |
3 4 5 |
|
|
Вычисление работы при разных способах описания движения также будет отличаться.
Закон движения задан в векторной форме |
|
|||||||
Если учесть, что |
|
7 ⁄ |
|
3 ∙ 7 |
, и тогда |
|||
3 |
|
, то |
|
|
|
|||
|
7 ∙ 7 |
|
|
|
|
|
||
/012 |
|
7 |
|
|
|
|
|
(7.4) |
|
|
|
|
. |
(7.5) |
|||
При |
из |
(7.5) следует, |
что |
|
|
|
||
|
3 |
∙ 8 7 |
7 |
|
9 ∙ ∆7 |
|
||
Закон движения задан в аналитической форме
|
R |
R |
R |
R |
R |
R |
R |
R |
Пусть |
F |
= Fxi |
+ Fy j |
+ Fz k , |
v |
= vx i |
+ vy j |
+ vz k . |
38
|
N = F v |
|
+ F v |
|
+ F v |
|
= F |
dx |
+ F |
dy |
+ F |
dz |
|
|
Тогда |
|
|
|
|
|
|
||||||||
x |
x |
y |
y |
z |
z |
x dt y dt |
z dt . |
|||||||
Тогда путем интегрирования мощности получаем, что работа равна |
||||||||||||||
|
3 ;; 5 6 |
(7.7) |
||||||||||||
Закон движения задан в естественной форме
Поскольку |
R |
R |
&R |
& |
v |
= vττ |
= sτ , то |
N = Fτ vτ = Fτ s . |
Отсюда следует, что при разложении силы по естественному базису мощность имеет только составляющая силы, направленная по касательной к траектории.
Тогда путем интегрирования мощности получаем, что работа равна |
|
|
3 |
<2 |
(7.9) |
/012, получаем, что |
|
|
Когда проекция силы на касательную к траектории постоянна, то есть < |
||
3 |
<2 |
(7.10) |
7.2. ЧАСТНЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ МОЩНОСТИ И РАБОТЫ
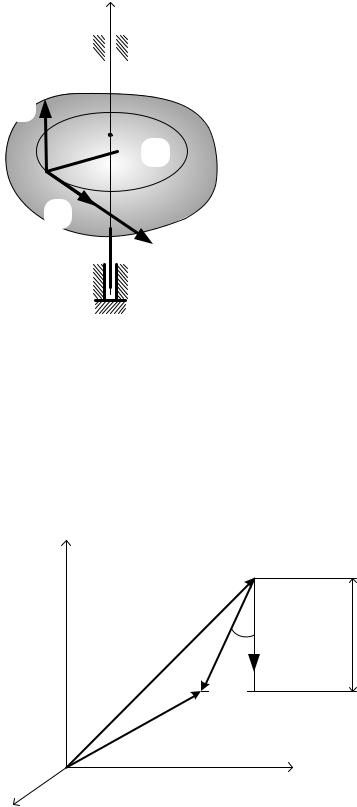
Работа силы, действующей на вращающееся тело
Силу, действующую на вращающееся тело (рис. 7.2), разложим на составляю- |
|||||||||||
щие по естественным осям: |
|
|
|
|
|
||||||
|
< |
1 |
|
=. |
4 > |
, |
|||||
|
|
|
|
|
|
|
|
|
|||
Мощность имеет только |
<. |
Мощность ее равна |
< , где |
. |
|||||||
|
4 > |
, |
|
|
|
|
56 |
|
|
||
Следовательно, |
|
< |
|
, но |
< |
|
|
. |
|
|
|
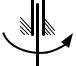
Таким образом, мощность силы равна произведению момента силы относи-
тельно оси вращения на угловую скорость тела:
4 > 56,.
z
 ω
ω
F b
 F n
F n
F τ
R
v
Рис. 7.2
39
Знак '+'соответствует случаю разгоняющей силы, а '-'─ тормозящей силы.
Если на тело действует не сила, а пара сил с вращающим моментом М, то его мощность определя-
ется аналогично: 4 >;,. |
|
(7.11) |
|
работа момента |
3 4 >; ? |
|
|
Если учесть, что |
, то элементарная ра- |
||
бота будет равна |
, ?⁄ |
, а полная |
|
получится путем интегрирования: |
|||
3 > ? ; ?. |
|
(7.12) |
|
Откуда при; /012 получится, что |
3 >;?. |
||
Работа силы тяжести
Сила тяжести постоянна по величине и по направлению, поэтому для вычисле- |
||||||||
|
|
|
3 ∙ 87 |
7 |
|
9 |
∙ ∆7 |
|
ния работы применим формулу (7.5): |
|
|
|
|
. |
|||
z |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 0 |
|
G |
h |
|
|
|
|
|
α |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
r
r
y
x
Рис. 7.3
Тогда
Поскольку
(7.13)
3 @ |∆7| /02 A |
3B >@ > B . |
|∆7| /02 A , то |
Знак '+'соответствует опускающемуся, а '─' ─ его подъему.
