
6038
.pdf
|
7 вариант |
|
|
|
8 вариант |
|
|
||
|
|
|
|
|
|
||||
Найти |
экстремум, |
используя |
Найти |
экстремум, |
используя |
||||
матричные формы записи процессора матричные формы записи процессора |
|||||||||
MathCAD: |
166 |
|
32 |
MathCAD: |
204 |
|
7 |
||
|
|
|
|
||||||
с = S141T |
= S22T |
с = S105T |
= S3T |
||||||
|
178 |
0.8 |
16 |
|
308 |
0 |
4 |
||
|
0.3 |
0.1 |
T |
|
0.9 |
0.1 |
T |
||
a = S0.63 |
0.5 |
0 |
a = S0.2 |
0.4 |
0 |
||||
|
0.9 |
0.2 |
0.4 |
|
|
0.8 |
0.2 |
0.8 |
|
|
9 вариант |
|
|
|
10 вариант |
|
|||
|
|
|
|
|
|
||||
Найти |
экстремум, |
используя |
Найти |
экстремум, |
используя |
||||
матричные формы записи процессора матричные формы записи процессора |
|||||||||
MathCAD: |
106 |
|
23 |
|
MathCAD: |
14 |
|
700 |
|
|
|
|
|
|
|
||||
с = S104T |
= S29T |
с = S35T |
= S300T |
||||||
|
107 |
0 |
17 |
|
|
38 |
0.1 |
400 |
|
|
0.2 |
0.1 |
|
|
0 |
0.3 |
|
||
a = S 0 |
0.2 |
0.3T |
|
a = S0.5 |
0 |
0.4T |
|
||
|
0.9 |
0.2 |
0.4 |
|
|
0.8 |
0.2 |
0.8 |
|
30
5 Каноническое представление при решении задач линейного программирования
Возможность получения из предложенной формы задачи линейного программирования любой другой формы − одна из прерогатив линейного программирования. Часто необходимостью является приведение задачи к каноническому виду представления.
Происходит преобразование неравенства в равенство путем установки в левой части уравнения заданной неотрицательной переменной. При этом если неравенство "меньше или равно", вводимая дополнительная переменная имеет знак минус, если "больше или равно", то знак плюс.
Дополнительная (фиктивная) переменная вводится в неравенство: |
|
≤ |
|
∙ + ∙ + + ∙ U≥V |
∙ |
! = 9 ∙ 9 ∙ 9 9 |
|
∙ + ∙ + + ∙ U+V = |
|
Уравнение принимает вид: |
|
9 |
|
Каждое из уравнений рассчитываемой системы уравнений необходимо уравновесить вводимой переменной. Система уравнений становиться преобразованной системой ограничений.
Условие неотрицательности соблюдается заменой разностью неотрицательных |
|
переменных W = W 9 X, |
W ≥ 0, X ≥ 0 |
Когда правая часть ограничений отрицательная, она умножается на отрицательную единицу.
В том случае, когда решалась задача поиска максимума, то быстро решить обратную ей задачу можно умножением целевой функции на минус = 9 . Таким образом − задача поиска на максимум, поиска на минимум.
31

5.1 Пример выполнения задания
Описание в общей форме математически поставленной задачи линейного
программирования. Рассматриваем и анализируем условия задачи. |
||
1 = 9x + 2 ∙ x → min |
||
329x∙ x +x+x ≤≥03 |
|
|
|
x 9 x = 1 |
|
Второй путь решения задачиx: |
≥преобразовав0, x ≥ 0 |
в ограничения-равенства систему |
ограничений-неравенств и введением дополнительной переменной система уравнений
принимает канонический вид и доступна для решения в математическом процессоре |
|
MathCAD в общепринятом для математиков виде. |
|
329x∙ x +x+x +x9xDD==03 |
|
В системе MathCAD вводятся записьx 9 xзадачи= 1 |
в общем виде и функция цели. Для |
решения используется встроенный блок Given 9 Minimize. После задания системы
ограничений и решения задачи находится величина функции цели и ее оптимальное значение.
Общий вид документа решения задачи в общей форме и в каноническом виде записи уравнений представлен ниже.
32

5.2 Задания для самостоятельной работы
1 вариант |
2 вариант |
|
|
Используя встроенные матричные |
Используя встроенные матричные |
операторы процессора MathCAD, привести |
операторы процессора MathCAD, привести |
уравнения в канонический вид и решить |
уравнения в канонический вид и решить |
их: |
их: |
x 9 6 ∙ x ≥ 6 |
x 9 5 ∙ x ≥ 10 |
F92 ∙ x + x ≤ 2 |
F9x 9 2 ∙ x ≤ 6 |
x ≥ 0, x ≥ 0 |
x ≥ 0, x ≥ 0 |
1(x) = x + 2 ∙ x → max(min) |
1(x) = 2 ∙ x + x → max(min) |
3 вариант |
|
4 вариант |
|
|
|
Используя встроенные матричные |
Используя встроенные матричные |
|
операторы процессора MathCAD, привести |
операторы процессора MathCAD, привести |
|
уравнения в канонический вид и решить |
уравнения в канонический вид и решить |
|
их: |
их: |
|
x 9 2 ∙ x ≥ 8 |
F |
2 ∙ x 9 3 ∙ x ≥ 12 |
F92 ∙ x + x ≤ 2 |
x + x ≤ 10 |
|
x ≥ 0, x ≥ 0 |
|
x ≥ 0, x ≥ 0 |
1(x) = 3 ∙ x + x → max(min) |
1(x) = x 9 x → max(min) |
|
|
5 вариант |
6 вариант |
|
|
|
||
Используя встроенные матричные |
Используя встроенные матричные |
||
операторы процессора MathCAD, привести |
операторы процессора MathCAD, привести |
||
уравнения в канонический вид и решить |
уравнения в канонический вид и решить |
||
их: |
|
их: |
|
F |
x 9 5 ∙ x ≤ 20 |
9x + 3 ∙ x ≥ 12 |
|
9x + x ≥ 9 |
F x 9 4 ∙ x ≤ 8 |
||
x ≥ 0, x ≥ 0 |
x |
≥ 0, x ≥ 0 |
|
1(x) = 3 ∙ x + 4 ∙ x → max(min) |
1(x) = x |
+ 5 ∙ x → max(min) |
|
33

7 вариант |
|
8 вариант |
|
|
|
||
Используя встроенные матричные |
Используя встроенные матричные |
||
операторы процессора MathCAD, привести |
операторы процессора MathCAD, привести |
||
уравнения в канонический вид и решить |
уравнения в канонический вид и решить |
||
их: |
|
их: |
|
96 ∙ x!x ≥ 12 |
|
2 ∙ x 9 x ≥ 6 |
|
Fx |
9 2 ∙ x ≤ 10 |
|
F9x + 3 ∙ x ≤ 9 |
x |
≥ 0, x ≥ 0 |
1(x) |
x ≥ 0, x ≥ 0 |
1(x) = 3 ∙ x + x → max(min) |
= x + x → max(min) |
||
|
9 вариант |
|
10 вариант |
|
|
||
Используя встроенные матричные |
Используя встроенные матричные |
||
операторы процессора MathCAD, привести |
операторы процессора MathCAD, привести |
||
уравнения в канонический вид и решить |
уравнения в канонический вид и решить |
||
их: |
|
их: |
|
F |
93 ∙ x + 4 ∙ x ≤ 12 |
F |
3 ∙ x 9 4 ∙ x ≥ 12 |
2 ∙ x 9 x ≥ 10 |
9x + x ≤ 1 |
||
|
x ≥ 0, x ≥ 0 |
|
x ≥ 0, x ≥ 0 |
1(x) = x + 3 ∙ x → max(min) |
1(x) = x + x → max(min) |
||
34
6 Математическая модель целочисленной задачи линейного программирования
Часто при проведении сложных математических исчислений результат может быть выполнен только в целых числах - число людей, машин, планет, траекторий полетов...
Данный тип задач необходимо решать способами целочисленного программирования. Целочисленное программирование требует буквального указания, что результат
поиска оптимальных значений может получать только целые значения.
Линейное программирование целочисленной задачи принимает вид математической
модели: |
|
|
|
|
|
|
|
|
|
|
→ max(min) |
|
|
|
1( ) = %& |
|
||||
Ограничения при этом выглядят следующим образом. |
|
|||||
|
≤ |
(≥) , = 1 … ( |
|
|||
%& |
|
|||||
|
|
≥ 0, Z = 1 … |
|
|
||
|
|
|
|
|
|
|
|
|
- целые, |
|
|
||
|
|
|
|
|
||
|
которые при решении задачи может принять переменная |
|
||||
То есть ряд значений, |
|
|
|
Z = 1 … |
|
|
определен заранее. Причем, если |
< , задача линейного программирования является |
|||||
частично целочисленной, если же = |
− полностью целочисленной. |
|
||||
При решении задач оптимизации классическими являются задачи целочисленного программирования: задача о наполнении ранца школьными предметами (или задача о рюкзаке), задача о раскрое материала, задача о коммивояжере.
Линейное программирование целочисленного исчисления при решении графическими методами начинается с построения линий ограничений на плоскости. После определения точки пересечения вершины многоугольника с целевой функцией, удовлетворяющей условию оптимальности, внутри определенной части плоскости строится еще один многоугольник, вершины которого имеют только целочисленные координаты.
Точка пересечения линии уровня целевой функции и вершины полученного многоугольника является оптимальным решением задачи целочисленного линейного программирования.
35

6.1 Пример работы в математическом процессоре MathCAD - выполнения методом графического решения оптимального целочисленного исчисления
Представлена математическая модель задачи оптимизации. Линейное программирование целочисленного решения задачи будет производиться графическим методом.
Устанавливается минимизируемая целевая функция и задается система ограничесний.
Производится построение допустимых областей значений для всех трех ограничений. Сначала записывается ограничение, затем выполняется выражение переменной из всех ограничении и отображаются в координатных осях геометрические изображения ограничений.
В первом графике рассматривается нижняя полуплоскость, потому что ограничением задано "меньше или равно". Второе и третье ограничение используют неравенство "больше или равно", поэтому исследуются верхние полуплоскости.
36
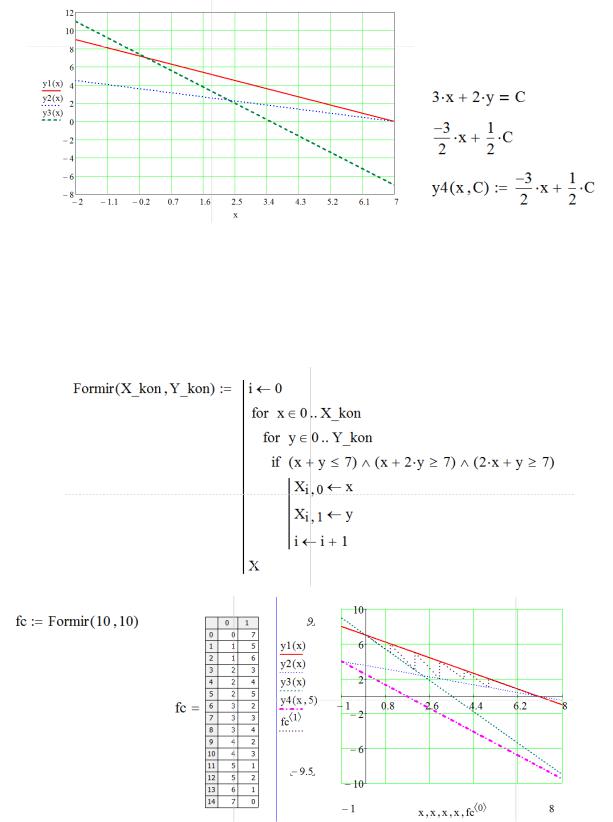
На одном графике строятся все три прямые, в середине явственно видна плоскость включения области допустимых значений. Применяя производную константу можно вывести уравнение линии, определяющей уровень целевой функции.
Для координат x и y находятся соответственно возможные значения экстремума
 .
.
Записывается программный модуль поиска и получения массива значений координат, численные величины которых могут выражены только в целочисленном варианте.
37

После рассмотрения построенных линий уровня определяется куда направлен антиградиент. Видно, что в пересечении линий и их минимального значения в точке V(2,3) можно найти целое число минимального решения задачи − оно равно f(2,3) = 12.
38
6.2 Задания для самостоятельного решения задачи оптимизационного целочисленного исчисления графическими методами
|
|
1 вариант |
|
|
|
2 вариант |
|
||||
|
|
|
|
||||||||
Представленную |
математическую |
Представленную |
математическую |
||||||||
модель |
задачи |
оптимизации |
следует |
модель |
задачи |
оптимизации |
следует |
||||
решить графическим методом при помощи |
решить графическим методом при помощи |
||||||||||
математического процессора MathCAD: |
математического процессора MathCAD: |
||||||||||
|
3 |
3 ∙ x + 2 ∙ x ≤ 7 |
|
|
|
x 9 4 ∙ x ≤ 4 |
|
||||
|
x + 2 ∙ x ≥ 6 |
|
|
* |
3 ∙ x + 2 ∙ x ≤ 6 |
|
|||||
|
|
x |
x 9 x |
≤ 3 |
|
|
9x + x ≤ 1 |
|
|||
|
|
≥ 0, x ≥ 0 |
|
|
|
x + 2 ∙ x ≥ 4 |
|
||||
|
1 = x + x |
→ max |
|
|
|
x |
≥ 0, |
x ≥ 0 |
|
||
|
|
|
|
|
|
|
1 = 3 ∙ x + 3 ∙→ max |
|
|||
|
|
3 вариант |
|
|
|
4 вариант |
|
||||
|
|
|
|
||||||||
Представленную |
математическую |
Представленную |
математическую |
||||||||
модель |
задачи |
оптимизации |
следует |
модель |
задачи |
оптимизации |
следует |
||||
решить графическим методом при помощи |
решить графическим методом при помощи |
||||||||||
математического процессора MathCAD: |
математического процессора MathCAD: |
||||||||||
|
|
x + x ≤ 14 |
|
|
9x + 10 ∙ x ≥ 8 |
|
|||||
|
33 ∙ x 9 5 ∙ x ≤ 15 |
|
|
8 ∙ x + 5 ∙ x ≤ 80 |
|
||||||
|
5 ∙ x + 3 ∙ x ≥ 21 |
|
|
* |
x 9 2 ∙ x ≤ 2 |
|
|||||
|
|
x |
≥ 0, x ≥ 0 |
|
|
|
x + 4 ∙ x ≥ 4 |
|
|||
|
1 = 7 ∙ x + x → max |
|
|
|
x |
≥ 0, |
x ≥ 0 |
|
|||
|
|
|
|
|
|
|
1 = x 9 x → max |
|
|||
|
|
5 вариант |
|
|
|
6 вариант |
|
||||
|
|
|
|
||||||||
Представленную |
математическую |
Представленную |
математическую |
||||||||
модель |
задачи |
оптимизации |
следует |
модель |
задачи |
оптимизации |
следует |
||||
решить графическим методом при помощи |
решить графическим методом при помощи |
||||||||||
математического процессора MathCAD: |
математического процессора MathCAD: |
||||||||||
|
|
|
x + x |
≤ 3 |
|
|
|
x 9 x ≥ 93 |
|
||
|
|
35 ∙ x + x ≥ 5 |
|
|
6 ∙ x + 7 ∙ x ≤ 42 |
|
|||||
|
|
x + 5 ∙ x ≥ 5 |
|
|
* |
2 ∙ x 9 3 ∙ x ≤ 6 |
|
||||
|
0 ≤ x |
≤ 4, 0 ≤ x ≤ 4 |
|
|
|
x |
x + x ≥ 4 |
|
|||
|
1 = 7 ∙ x 9 x → max |
|
|
|
≥ 0, |
x ≥ 0 |
|
||||
|
|
|
|
|
|
|
1 = 2 ∙ x 9 x → max |
|
|||
39
