Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5545

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

629.33 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Пример. Построить прямую l : 3y + 6 = 0.

Решение. Уравнение прямой l является общим уравнением прямой на плоскости A = 0 , B = 3, C = 6 , параллельной оси Ox и проходящей через точку

( 0;−2). (См. рис. 21).

		0	x

	l	-2	Рис. 21
			Рис. 21
4. При A ¹ 0 , B = 0 , C ¹ 0		уравнение (3.2) примет вид: Ax + C = 0 или

x = − C . A

Это уравнение прямой на плоскости параллельной оси Oy и проходящей

	−	C
через точку			; 0 . (См. рис. 22)
через точку			; 0 . (См. рис. 22)
		A

−	C	0	x
	C
	A	Рис. 22
	A

Пример. Построить прямую l : 2x +1 = 0 .
Решение. Уравнение прямой l является			общим уравнением прямой на

плоскости A = 2 , B = 0 , C = 1 параллельной оси Oy и проходящей через точку

−	1
		; 0	. (См. рис. 23)
	2	; 0	. (См. рис. 23)
	2
					y
					y
			−	1	0	x
				1

			2
						Рис. 23

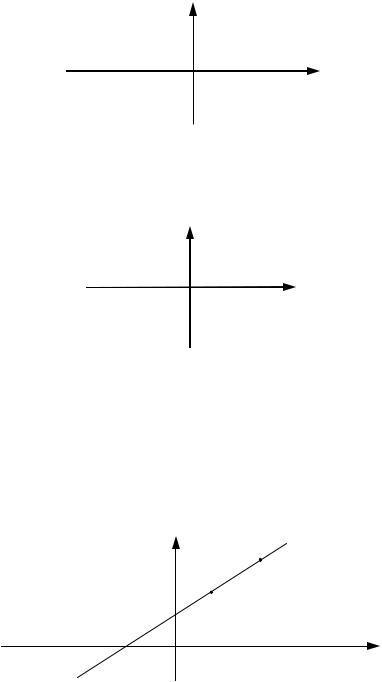
5. При A = 0 , B ¹ 0 , C = 0 уравнение (3.2) примет вид: By = 0 или y = 0. Это уравнение координатной оси Ox (См. рис. 24)

0	x
	Рис. 24

6. При A ¹ 0 , B = 0 , C = 0 уравнение (3.2) примет вид: Ax = 0 или x = 0 . Это уравнение координатной оси Oy . (См. рис. 25)

0	x
	Рис. 25
Итак, рассмотрены все возможные случаи общего уравнения (3.2) прямой на
плоскости.
Выведем уравнение прямой l ,	проходящей через две заданные точки
M1 (x1; y1 ) и M 2 (x2 ; y2 ) на плоскости	xOy в прямоугольной декартовой системе
координат. (См. рис. 26)
y
	M 2
	M1
l	x
	Рис. 26
Поскольку точка M1 (x1 ; y1 ) лежит на прямой l то, подставляя x = x1		и y = y1
в уравнение (3.5), находим, что уравнение прямой l имеет вид:
l : y - y1 = k ×(x - x1 ),		(3.6)
где k – пока неизвестный коэффициент.

Так как прямая l проходит и через точку M 2 (x2 ; y2 ), то ее координаты должны удовлетворять уравнению (3.6), то есть:

- y

= k × (x

- x ), откуда k =

y2 − y1

x2 − x1

Подставляя найденное значение k

в уравнение (3.6), получим уравнение прямой,

проходящей через точки M1

и M 2 :

l :

y − y1

x − x1

(3.7)

x2 − x1

y2 − y1

Пример. Составить уравнение прямой l ,

проходящей через точки M1 (1; 2) и

M 2 (-1;3).

Решение. Подставляя в уравнение (3.7)

x1 =1, y1 = 2 и

x2 = -1, y2 = 3,

находим искомое уравнение прямой

l :

y − 2

x −1

;

y − 2

x −1

;

- 2(y - 2) =1× (x -1);

− 2 y + 4 = x −1,

3 − 2

−1−1

− 2

следовательно, l : x + 2 y − 5 = 0 .

Ответ: x + 2 y − 5 = 0.

Взаимное расположение прямых на плоскости

Пусть две прямые l1 и l2

заданы уравнениями с угловыми коэффициентами k1

и k2 ,

соответственно,

то есть

l1 : y = k1 x + b1 ;

l2 : y = k2 x + b2 .

Требуется найти

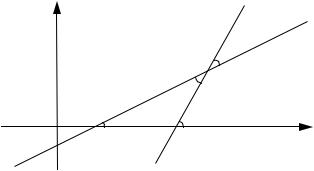
угол ϕ , на который надо повернуть прямую l , вокруг точки их пересечения до совпадения с прямой l2 . (См. рис.27)

y	l2	l1
	ϕ	l1
	ϕ
	α2
0	α1
0	Рис. 27	x
	Рис. 27

По теореме	о внешнем угле	треугольника, имеем: α2 = ϕ + α1 или
ϕ = α2 − α1 . Если ϕ ¹ 90 , то
	tgϕ = tg(α 2 -α1 )		=		tgα2 − tgα1			.
	tgϕ = tg(α 2 -α1 )		=		+ tgα1	×tgα		.
			1		+ tgα1	×tgα	2
Но так как tgα1 = k1	и tgα 2 = k2 , то
	tgϕ	=		k2 − k1			(3.8)
	tgϕ	=	1 + k1 × k2				(3.8)

Таким образом, формула (3.8) позволяет находить угол между двумя прямыми на плоскости.

Пример. Найти угол между прямыми l1 : x − 2 y + 1 = 0 и l2 : 3x + y − 3 = 0 . Решение. Запишем общее уравнение заданных прямых l1 и l2 в виде

уравнений с угловыми коэффициентами k1 и k2 , соответственно:

l : 2 y = x +1 или l : y =										1	x +	1	, значит k =									1	;
l : 2 y = x +1 или l : y =											x +		, значит k =										;
1						1	2				2							1			2
							2				2										2
l2 : y = −3x + 3 , значит k2 = −3.
Подставляя найденные значения k =																1	и k				= −3 в формулу (3.8), находим
Подставляя найденные значения k =																	и k			2	= −3 в формулу (3.8), находим
													1		2					2
															2
угол ϕ между прямыми l1							и l2 :
	- 3 -				1		-	7
	- 3 -						-	2
tgϕ =		2				=		2	= 7 , откуда ϕ = arctg 7 .
tgϕ =						=			= 7 , откуда ϕ = arctg 7 .
	1+		1	× (- 3)			-	1
	1+			× (- 3)			-
	2						2
Ответ: ϕ = arctg 7 .
Заметим, что если требуется вычислить острый угол между прямыми, то
правая часть формулы (3.8) берется по модулю, то есть
											tgϕ =				k2 - k1				.
															k2 - k1
														1 + k × k				2
															1			2

Если прямые l1 : y = k1 x + b1 ; l2 : y = k2 x + b2 параллельны, то ϕ = 0 и

tgϕ = 0 , следовательно, из формулы (3.8) получаем, что k2 − k1 = 0, то есть k2 = k1 .

И обратно, если прямые l1					и l2 таковы, что k1 = k2 , значит tgϕ = 0 , то есть прямые
параллельны.
Если прямые l			и l	2	перпендикулярны, то ϕ = π , следовательно
1							2

ctgϕ =	1 + k1 × k2	= 0	, откуда k × k				= -1. Справедливо и обратное утверждение.
						2
	k2 − k1				1

Пример. Составить уравнение прямой l , проходящей через точку M (1; 2) и

перпендикулярной прямой L : 3x + 2 y − 5 = 0 .

Решение. Перепишем общее уравнение прямой L в виде уравнения прямой с

угловым коэффициентом kL :

L : 3x + 2 y − 5 = 0 ,

2 y = −3x + 5 ,

y = −

x +

, значит k

= −

Прямые l и L перпендикулярны по условию, значит kl × kL = -1,

следовательно, k

= −

Подставляя в уравнение (3.5) kl =

, x0 = 1,

y0 = 2 находим искомое

уравнение прямой l :

l : y − 2 = 2 (x −1) 3

l : 3y − 6 = 2x − 2

l : 2x − 3y + 4 = 0

Ответ: 2x − 3y + 4 = 0.

§4. Функция одного переменного. Основные понятия

Понятие функции является одним из главных понятий математики. С этим понятием часто встречаемся в природе, изучая различные процессы и явления.

Пусть D – некоторое множество действительных чисел. Если каждому числу

x D – поставлено в соответствие	по какому-то правилу или	закону f
единственное действительное число y ,	то говорят, что на множестве	D задана

функция одного переменного и обозначается: y = f (x). Число x D называется аргументом функции, y – значением функции, множество D – областью определения функции, множество всех значений y , которые соответствуют числам множества D – областью значений функции – E . (См. рис. 28)

E		y = f (x)
y
	D
0	x	x

Рис. 28

Графиком Г( f ) функции y = f (x) называется множество всех точек (x, y)

плоскости xOy таких, что x D , а y = f (x), то есть

Г( f ) = {(x, y) x D, y = f (x)}.

Далее будем задавать функцию одного переменного аналитически, то есть с помощью формулы. В этом случае под областью определения D функции понимают множество всех тех значений x , для которых данная формула имеет смысл.

Пример. Формула y = x 2 задает функцию y	одного переменного x .
Поскольку данная формула имеет смысл при всех	действительных значениях

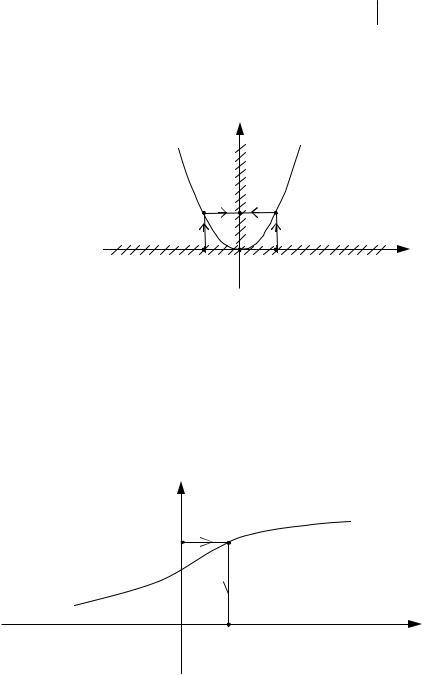
переменной x , то область определения D данной функции есть множество всех действительных чисел R , то есть D = R. Так как квадрат действительного числа – число неотрицательное, то множество значений E данной функции y = x 2 есть множество всех неотрицательных чисел, то есть E = {y y ³ 0}. Графиком функции

y = x 2	является парабола в плоскости xOy с вершиной в точке O ,				ветви которой
направлены в положительном направлении оси Oy . (См. рис. 29)
	y		E	y = x2
				y = x2

		1
				D
	-1	0	1	x
			Рис. 29
Пусть задана функция y = f (x), x D ,				такая, что для x1 ¹ x2 , f (x1 ) ¹ f (x2 ), то
есть	для любого y E найдется	единственное x D такое, что			f (x) = y или
x = f −1 (y). Тем самым определена функция				f −1 , называемая функцией, обратной к
функции f . (См. рис. 30)

y = f (x)

0 x = f −1 (y) x

Рис. 30

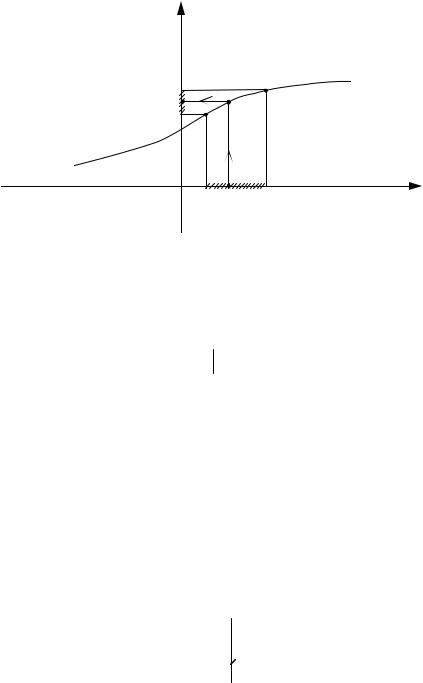
Покажем как строим график обратной функции. Если для обратной функции обозначить аргумент через x , а функцию через y , то графики функций y = f (x) и x = f −1 (y) совпадают. Разница состоит лишь в том, что для функции y = f (x) ось

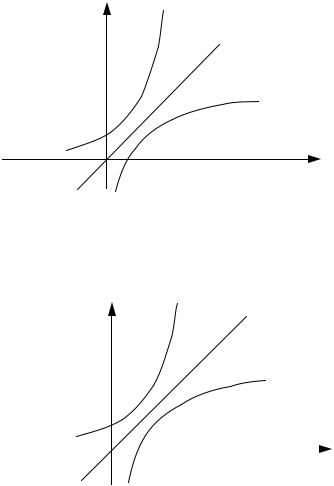
Ox – ось абсцисс, а ось Oy – ось ординат, а для функции x = f −1 (y) роль осей меняется.

Если же обозначить аргумент обратной функции через x , а значение функции через y , то получается иной график. Именно, нужно перевести друг в друга оси Ox и Oy . Это делается с помощью отражения всей плоскости xOy относительно биссектрисы первого координатного угла, то есть прямой y = x . При этом отражении график функции y = f (x) переходит в график обратной функции

y = f −1 (x).

Итак, график обратной функции относительно прямой y = x . (См. рис.31)

симметричен графику заданной функции

y = f −1 (x)

y = x

y = f (x)

Рис. 31 x

Пример. Функция y = ex является обратной функцией к функции y = ln x .

(См. рис. 32)

y = ex

y = x

y = ln x

0 1	x
	Рис. 32

Основные элементарные функции

Следующие шесть типов функции называются основными элементарными функциями:

I. Постоянная функция y = C – функция, ставящая в соответствие каждому действительному числу x одно и то же число C . (См. рис. 33) D = R , E = {C}.

		y = C
C
0	x	x

Рис. 33

II. Степенная функция y = xα .

а) α – целое число.

Если α – четное, то D = R , E = { y y ³ 0}.

y = xα (α - четное, целое)

0	x
	Рис. 34
Если α – нечетное, то D = R , E = R .
y	y = xα (α - нечетное, целое)

0		x
		Рис. 35
Графики функции	y = x−α	(α – целое)	показаны на рис. 36 и рис. 37
соответственно.
В случае если α –	четное,	D = R \ {0} –	множество всех действительных

чисел, кроме нуля, E = { y y > 0}.

y = x−α (α - четное)

0	x
	Рис. 36
В случае если α –	нечетное, D = R \ {0}, E = R \ {0}.
y	y = x−α (α - нечетное)
	y = x−α (α - нечетное)

0	x
	x
	Рис. 37

б) α – рациональное, то есть α = m , m, n Ζ , n ¹ 0 ;

y = xα = x

= n

или y =

. (См. рис. 38). D = { x

x ³ 0},

Пример графика функции y = x

E = { y

y ³ 0}.

y = x 2

0 1

Рис. 38

или y = 3 x2

Пример графика функции y = x

.(См. рис.39).

D = R , E = {y y ³ 0}.

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023628.44 Кб05540.pdf
#
21.11.2023628.55 Кб05541.pdf
#
21.11.2023628.8 Кб05542.pdf
#
21.11.2023628.84 Кб05543.pdf
#
21.11.2023629.17 Кб05544.pdf
#
21.11.2023629.33 Кб05545.pdf
#
21.11.2023629.37 Кб05546.pdf
#
21.11.2023629.58 Кб05547.pdf
#
21.11.2023629.79 Кб05548.pdf
#
21.11.2023629.88 Кб05549.pdf
#
21.11.2023130.09 Кб0555.pdf