1manly_b_f_j_statistics_for_environmental_science_and_managem

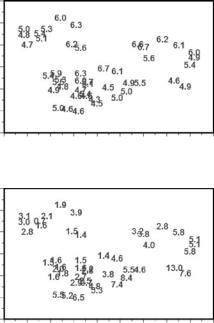
Figure 9.1

Location of 45 nests of Messor wasmanni (species 1) and 15 nests of Cataglyphis bicolor (species 2) in a 240 × 250-ft study area.

of the ant Messor wasmanni and 15 nests of the ant Cataglyphis bicolor in a 240 × 250-ft area (Harkness and Isham 1983; Särkkä 1993, Figure 5.8). Messor (species 1) collects seeds for food, while Cataglyphis (species 2) eats dead insects, mostly Messor ants.

Possible questions here are basically the same as for the shellfish:

•Are the positions of the Messor wasmanni nests randomly located over the study area, or is there evidence of uniformity or clustering in the distribution?

•Similarly, are the Cataglyphis bicolor nests random, uniform, or clustered in their distribution?

•Is there any evidence of a relationship between the positions of the nests for the two species, for example, with Messor wasmanni nests tending to be either close to or distant from the Cataglyphis bicolor nests?

In this second example there is a point process for each of the two species of ant. It is apparent that this could be made similar to the first example because it would be possible to divide the ant study area into quadrats and compare the two species by quadrat counts, in the same way as for the shellfish. However, knowing the positions of the points instead of just how many are in each quadrat means that there is more information available in the second example than there is in the first.

A third example comes from the Norwegian research program that was started in 1972 in response to widespread concern in Scandinavian countries

In considering these three examples, the most obvious differences between them are that the first concerns counts of the number of shellfish in quadrats, the second concerns the exact location of individual ant nests, and the third concerns the measurement of variables at lakes in particular locations. In addition, it can be noted that the shellfish and lake examples concern sample data in the sense that values could have been recorded at other locations in the study area, but this was not done. By contrast, the positions of all the ant nests in the study area are known, so this is population data.

9.3  Spatial Patterns in Quadrat Counts

Given a set of quadrat counts over an area, such as those for the pipis in Table 9.1, there may be interest in knowing whether there is any evidence for a spatial pattern. For example, there might be a tendency for the higher counts to be close together (clustering) or to be spread out over the study area (uniformity). The null hypothesis of interest is then randomness, in the sense that each of the counts could equally well have occurred in any of the spatial locations. This question has been of particular interest to those studying the spatial distribution of plants, where distributions may appear to be random for some quadrat sizes but not for others (Mead 1974; Galiano et al. 1987; Dale and MacIsaac 1989; Perry and Hewitt 1991; Perry 1995a, 1995b, 1998).

A particular hypothesis that it is sometimes of interest to test is complete spatial randomness, in which case the individual items being counted over a large area are each equally likely to be anywhere in the area, independently of each other. Then, it is a standard result that the counts in quadrats will have a Poisson distribution. That is, the probability of a count x is given by the equation

where μ is the expected value (mean) of the counts.

One of the characteristics of the Poisson distribution is that the variance equals the mean. Therefore, if x and s2 are the mean and variance, respectively, of a set of quadrat counts, then the variance-to-mean ratio R = s2/x should be approximately 1. Values of R that are much less than 1 indicate that the counts are more uniform than expected from the Poisson distribution, so that there is some tendency for the individuals to spread out evenly over the study area. On the other hand, values of R much larger than 1 indicate that the counts are more variable than expected from the Poisson distribution, so that there is a tendency for individuals to accumulate in just a few of the quadrats, i.e., clustering.

A standard test for whether R is significantly different from 1 involves comparing

212 Statistics for Environmental Science and Management, Second Edition

with the t-distribution with n − 1 degrees of freedom (df). If a significant result is obtained, then R < 1 implies some evenness in the counts, while R > 1 implies some clustering in the counts.

Even when the quadrat counts do not follow a Poisson distribution, they can be randomly distributed in space, in the sense that the counts are effectively randomly distributed to the quadrats, independently of each other. In particular, there will be no tendency for the high counts to be close together, so that there is some clustering (positive spatial correlation), or for the high counts to be spread out, so that there is some evenness (negative spatial correlation). This hypothesis can be tested using a Mantel matrix randomization test (Mantel 1967).

If quadrat counts tend to be similar for quadrats that are close in space, then this can be expected to show up in a positive correlation between the spatial distance between two quadrats and the absolute difference between the counts in the quadrats. The following test is designed to see whether this correlation is significantly large.

Suppose that there are n quadrats, and let the spatial distance between quadrats i and j be denoted by dij. This distance can be calculated for every pair of quadrats to produce a matrix

of geographical distances. Because of the way that it is calculated, this matrix is symmetric, with di,j = dj,i and with zeros down the diagonal, as shown.

A second matrix

can also be constructed such that the element in row i and column j is the absolute difference

between the count for quadrat i and the count for quadrat j. Again, this matrix is symmetric.

Given these matrices, the question of interest is whether the Pearson correlation coefficient that is observed between the pairs of distances (d2,1, c2,1),

(d3,1, c3,1), (d3,2, c3,2), …, (dn,n−1, cn,n−1) in the two matrices is unusually large in comparison with the distribution of this correlation that is obtained if the

quadrat counts are equally likely to have had any of the other possible allocations to quadrats. This is tested by comparing the observed correlation with the distribution of correlations that is obtained when the quadrat counts are randomly reallocated to the quadrats.

Mantel (1967) developed this procedure for the problem of determining whether there is contagion with the disease leukemia, which should show up with cases that are close in space and tending to be close in time. He noted that, in practice, it may be better to replace spatial distances with their reciprocals and see whether there is a significant negative correlation between 1/di,j and ci,j. The reasoning behind this idea is that the pattern that is most likely to be present is a similarity between values that are close together rather than large differences between values that are distant from each other. By its nature, the reciprocal transformation emphasizes small distances and reduces the importance of large differences.

Perry (1995a, 1995b, 1998) discusses other approaches for studying the distribution of quadrat counts. One relatively simple idea is to take the observed counts and consider these to be located at the centers of their quadrats. The individual points are then moved between quadrats to produce a configuration with equal numbers in each quadrat, as close as possible. This is done with the minimum possible amount of movement, which is called the distance to regularity, D. This distance is then compared with the distribution of such distances that is obtained by randomly reallocating the quadrat counts to the quadrats, and repeating the calculation of D for the randomized data. The randomization is repeated many times, and the probability, Pa, of obtaining a value of D as large as that observed is calculated. Finally, the mean distance to regularity for the randomized data, Ea, is calculated, and hence the index Ia = D/Ea of clustering. These calculations are done as part of the SADIE (Spatial Analysis by Distance IndicEs) programs that are available from Perry (2008).

Example 9.1:  Distribution and Spatial Correlation for Shellfish

For an example, consider the pipi and cockle counts shown in Table 9.1. There are n = 88 counts for both species, and the mean and variance for the pipi counts are x = 19.26 and s2 = 2551.37. The variance-to-mean ratio is huge at R = 132.46, which is overwhelmingly significant according to the