Задача частично целочисленного линейного программирования. Метод гомори-2 Постановка частично целочисленной задачи линейного программирования (чцзлп).

Найти вектор x=(x₁...,x_n), что минимизирует целевую функцию

L(x)= c₁x₁ + ... + c_nx_n (10.1)

и удовлетворяет систему ограничений

a₁₁x₁ + . . . + a_1n x_n = a₁₀

. . . . . . . . . . . . . . . . . . . . . . . (10.2)

a_m1x₁ + . . . + a_mnx_n = a_m0

x_j0, j=1...,n (10.3)

x_j — цели, j=1...,p (pn). (10.4)

Изложение метода Гомори-2.

Метод Гомори-2, как и метод Гомори-1, является одним из методов отсечения и заключается в следующем.

Решается вспомогательная ЗЛП (10.1)–(10.3), которую получают из исходной ЗЛП (10.1)–(10.4) отбрасыванием условия целочисленности переменных (10.4). Если ее решение удовлетворяет условие (10.4), то он же является и решением исходной ЧЦЗЛП. Иначе от решения ЗЛП переходят к новой вспомогательной ЗЛП присоединением линейного ограничения, которое удовлетворяют целочисленные (в понимании условий (10.4)) развязки исходной ЧЦЗЛП, но не удовлетворяетполученное нецелочисленное решение исходной ЗЛП. Упомянутое дополнительноеограничение определяет некоторую отрезающую плоскость и называется правильным відтином. Присоединение новых правильных відтинів осуществляется до тех пор, пока на некотором шаге не будет получено целочисленное (в понимании условий (10.4)) решение вспомогательной задачи, которое и является оптимальным решением исходной ЧЦЗЛП. В методе Гомори-2 правильный відтин строится так.

Пусть на последней итерации симплекс-метода при решении вспомогательной ЗЛП ее непрямые ограничения приобрели вид:

x_i + Q_i,m+1 x_m+1 +...+ Q_in x_n = Q_i0, i=1...,m

и, значит, решением вспомогательной ЗЛП является вектор

x = ( Q₁₀...,Q_m0,0,...,0 ).

Пусть существует номер r (rp) такой, что Q_r0 — нецелое, и {z} — дробная часть z. Тогда правильный відтин методу Гомори-2имеет вид:

x_n+1 – D_r,m+1x_m+1 –...– D_rnx_n = – {Q_r0} (10.5)

где x_n+1  0 — дополнительная переменная, и

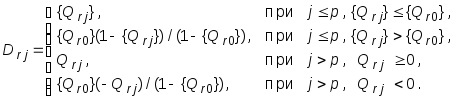(10.6)

Алгоритм метода Гомори-2.

1. Решаем вспомогательную ЗЛП (10.1)–(10.3). Пусть x(0) — ее оптимальное решение. Если эта задача не имеет решения, то исходная ЧЦЗЛП также не имеет решения.

2. Пусть на s-й итерации решена вспомогательная ЗЛП, что имеет M ограничений и N переменных, x(s) — ее оптимальное решение. Допустим, что x(s) определяется каноничными ограничениями последней итерации, а именно:

x_i + Q_i,M+1 x_M+1 +...+ Q_iN x_N = Q_i0, i=1...,M

откуда выплывает, что

x(s)= ( Q₁₀...,Q_M0,0,...,0 ).

3. Если Q_i0 (i=1...,p) — цели, то конец: x(s) является оптимальным решением исходной ЧЦЗЛП. Если существует хотя бы одно и такое, что _Qi0 — нецелое (i=1...,p), то переход к пункту 4.

4. Находим r=min{i}по всем и (i=1...,p) таким, что Q_i0 — нецелое и строим дополнительное ограничение за формулами (10.5)(10.6) при m=Mи n=N.

5. Расширяем симплекс-таблицу за счет (M+1) -ой строки (дополнительное ограничение) и (N+1) -го столбца, что отвечает дополнительной переменной xN+1.

6. Решаем расширенную ЗЛП с помощью двойственного симплекс-метода (ДСМ) и переходим к пункту 2 с заменой s на s+1, M на M+1, N на N+1. Если на некоторой итерации ДСМ одна из дополнительных переменных задачи опять становится базисной, то из последующего рассмотрения исключаются соответствующие ей строка и столбец и при переходе к пункту 2 заменяется лишь s на s+1.

Программное обеспечение.

Обучающий модуль, с помощью которого частично целочисленная задача линейного программирования Решается в диалоге с пользователем за выложенным алгоритмом, вызывается из раздела «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ» главного меню пакета ПО–МО.

Задание.

Решить методом Гомори-2задачи частично целочисленного линейного программирования, условия которых задаются модулем с помощью команды «Данные» главного меню (задачи №1–№9), а также следующие задачи.

1)	x1 + 8 x2  max	2)	– 6 x1 – x2  min
	3 x1 + x2  9		– 2.9 x1 + 6 x2  17.4
	0.16 x1 + x2  1.9		3 x1 – x2  1
	xj  0, xj — целое, j = 1,2;		xj  0, xj — целое, j = 1,2;

3)	0.25 x1 + x2  max	4)	– 2 x1 – 4 x2  min
	0.5 x1 + x2  1.75		2 x1 + x2  19.33
	x1 + 0.3 x2  1.5		x1 + 3 x2  10
	xj  0, xj — целое, j = 1,2;		xj  0, xj — целое, j = 1,2;

5)	x1 + x2  max	6)	x1 + x2  max
	2 x1 + 11 x2  38		2 x1 + 11 x2  38
	x1 + x2  7		x1 + x2  7
	4 x1 – 5 x2  5		4 x1 – 5 x2  5
	xj  0, j = 1,2, x2 — целое;		xj  0, j = 1,2, x1 — целое;

7))	x1  max	8)	– 8 x1 – 6 x2  min
	x1 + 3 x2  12		3 x1 + 5 x2 + x3 = 11
	3 x1 – 8 x2  24		4 x1 + x2 + x4 = 8
	xj  0, j = 1,2, x1 — целое;		xj  0, j = 1,2, x1 — целое.

Ответы:

1) x* = (2; 1), L(x*)= 10.

2) x* = (1; 3), L(x*)= –9.

3) x* = (1; 1), L(x*)= 1.25.

4) x* = (7; 1), L(x*)= –18.

5) x* = (3.75; 2), L(x*)= 5.75.

6) x* = (4; 2.73), L(x*)= 6.73.

7) x* = (9; 0.38), L(x*)= 9.

8) x* = (1; 1.6; 0; 2.41), L(x*)= –17.6.

Лабораторная работа 11.