Statistical physics (2005)

infinity. One thus has to return to equation (7.4).

–We have just studied the low temperature regime T TF , which takes place in metals at room temperature (TF 104 K) and corresponds to Fig. 7.3.

In astrophysics, the “white dwarfs” enter in this framework. They are stars at the end of their existence, which have already burnt all their nuclear fuel and therefore have shrunk. Their size is of the order of a planet (radius of about 5000 km) for a mass of 2 × 1030 kg (of the order of that of the sun), their temperature T of 107 K. Their high density in electrons determines εF . TF being in the 109 K range, the low temperature regime is achieved!

This regime for which the Quantum Statistics apply is called the “degenerate” (in opposition to “classical”) regime : as already mentioned about Pauli paramagnetism, and will be seen again below, the “active” particles all have an energy close to µ, this is almost as if this level was degenerate in the Quantum Mechanics meaning.

–On the other hand, when T TF , the integral (7.19) vanishes. This

is realized either at low density (εF small), or at given density when T tends to infinity. Then e−α tends to infinity, and since α = βµ with β tending to zero, this implies that µ tends to −∞. One then finds the Maxwell-Boltzmann Classical Statistics, as discussed in §6.7.2.

–Between these two extreme situations, µ thus decreases from εF to −∞ when the ratio T /TF increases.

When studying systems at room temperature, the regime is degenerate in most cases. For properties mainly depending on the Pauli principle, one can consider then to be at zero temperature. This is the situation when filling the electronic shells in atoms according to the “Aufbau (construction) principle”, widely used in Chemistry courses : the Quantum Mechanics problem is first solved in order to find the one-electron energy levels of the considered atom. The solutions ranked in increasing energies are the states 1s, 2s, 2p, 3s, 3p, 4s, 3d, etc. (except some particular cases for some transition metals). These levels are then filled with electrons, shell after shell, taking into account the level degeneracy (K shell, n = 1, containing at most two electrons, L shell of n = 2, with at most eight electrons, etc.). Since the energy splittings between levels are of the order of a keV for the deep shells and of an eV for the valence shell, the thermal energy remains negligible with respect to the energies coming into play and it is as if the temperature were zero.

On the other hand, if one is interested in temperature-dependent properties, like the specific heat or the entropy, which are derivatives versus temperature of thermodynamical functions, more exact expressions are required and at low temperature one will proceed through limited developments versus the variable T /TF .

7.2.2Specific Heat of Fermions

The very small contribution of electrons to a metal specific heat, which follow the Dulong and Petit law (see Ch. 2, §(2.4.5)) only introducing the vibrations of the lattice atoms, presented a theoretical challenge in the 1910s. This lead to a questioning of the electron conduction model, as proposed by Paul Drude in 1900.

To calculate the specific heat Cv =

Å∂U ã

∂T N,Ω

needs to express the temperature dependence of the internal energy.

One can already make an estimate of Cv from the observation of the shape of the Fermi distribution : the only electrons which can absorb energy are those occupying the states in a region of a few kB T width around the chemical potential, and each of them will increase its energy by an amount of the order kB T to reach an empty state.

The number of concerned electrons is thus kB T · D(µ) and for a three-

dimensional system at low temperature (kB T 1, so that µ and εF are

εF

close),

These considerations evidence a reduction of the value of Cv with respect to the classical value N kB in a ratio of the order kB T /µ 1, because of the very small number of concerned electrons.

The exact approach refers to a general method of calculation of the integrals in which the Fermi distribution enters : the Sommerfeld development. The complete calculation is given in Appendix 7.1. Here we just indicate its principle.

At a temperature T small with respect to TF , one looks for a limited development in T /TF of the fermions internal energy U , which depends of T , and of

164 Chapter 7. Free Fermions Properties

the chemical potential, itself temperature-dependent. The searched quantity

which is indeed of the form (7.24), as far as µ is not very di erent from εF (see Appendix 7.1).

The first factor in (7.25) is the specific heat of a monoatomic ideal gas; the last factor is much smaller than unity in the development conditions, it ranges between 10−3 and 10−2 at 300 K (for copper it is 3.6 × 10−3) and expresses the small number of e ective electrons.

The electron’s specific heat in metals is measured in experiments performed at temperatures in the kelvin range. In fact the measured total specific heat includes the contributions of both the electrons and the lattice

The contribution Cvlattice of the lattice vibrations to the solid specific heat was studied in Ch. 2, §2.4.5. The Debye model was mentioned, which correctly interprets the low temperature results by predicting that Cvlattice is proportional to T 3, as observed in non-metallic materials. The lower the temperature, the less this contribution will overcome that of the electrons.

From the measurement of γ one deduces a value of εF of 5.3 eV for copper whereas in §7.1.1 we calculated 7 eV from the value of the electrons concentration, using (7.7). In the case of silver the agreement is much better since the experiment gives εF = 5.8 eV, close to the prediction of (7.7).

The possible discrepancies arise from the fact that the mass m used in the theoretical expression of the Fermi energy was that of the free electron. Now a conduction electron is submitted to interactions with the lattice ions, with the solid vibrations and the other electrons. Consequently, its motion is altered,

which can be expressed by attributing it an e ective mass m . This concept will be explained in §8.2.3 and §8.3.3.

Defining

one deduces from these experiments a mass m = 1.32m for copper, m = 1.1m for silver, where m is the free electron mass.

Note that the fermion entropy can be easily deduced from the development of the Appendix : we saw that A = −P Ω (see §3.5.3), so that, according to

The electrons entropy thus satisfies the third law of Thermodynamics since it vanishes with T .

7.2.3Thermionic Emission

ε

0

V

εF

0 f (ε) 1

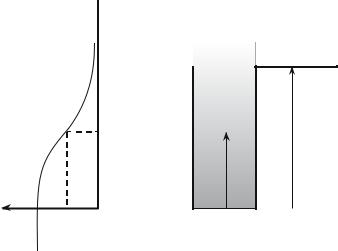
Fig. 7.4: Potential well for the electrons of a metal. In order to extract an electron at zero temperature, one illuminates the solid with a photon of energy higher than V − εF .

The walls of the “potential box” which confines the electrons in a solid are not really infinitely high. The photoelectrical e ect, evidenced by Heinrich

Hertz (1887), and interpreted by Albert Einstein (this was the argument for Einstein’s Nobel prize in 1921), allows one to extract electrons from a solid, at room temperature, by illumination with a light of high enough energy : for zinc, a radiation in the near ultraviolet is required (Fig. 7.4).

The energy’s origin is here the state of a free electron with zero kinetic energy, i.e., with such a conventionthe Fermi level has a negative energy. The potential barrier is equal to V . To extract an electron at zero temperature, a photon must bring it at least V − εF , an energy usually in the ultraviolet range.

When heating this metal to a high temperature T , the Fermi distribution is spreading toward little negative or even positive energies, so that a few electrons are then able to pass the potential barrier and become free (Fig. 7.5). One utilizes tungsten heated to about 3000 K to make the filaments of the electrons cannons of TV tubes or electronic microscopes, as its fusion temperature is particularly high (3700 K).

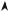ε

0

V

µ

f (ε) 1/2

Fig. 7.5: Filling of the electronic states in a metal heated to a high temperature T .

One way to calculate the thermal current consists in expressing that a particle escapes the metal only if it can overcome the potential barrier, i.e. if its kinetic energy in the direction perpendicular to the surface, taken as z axis, is large enough. It should satisfy

We know that the electronic energies, and thus V and V −µ, are of the order of a few eV : whatever the filament temperature, the system is in a regime

where kB T remains small with respect to the concerned energies, and where kB T

εF

the denominator exponent is large for the electrons likely to be emitted.

The Fermi distribution can then be approximated by a Maxwell-Boltzmann distribution

There remains to estimate the number ∆n of electrons moving toward the surface ∆S during a time ∆t. This is a standard problem of kinetic theory of gases (the detailed method of calculation is analogous to the kinetic calculation of the pressure, §4.2.2).

One obtains a total current jz = ∆n/∆S∆t equal to

This expression shows the very fast variation of the thermal emission current with the temperature T , in T 2e−(V −µ)/kB T . It predicts that a 0.3 × 0.3 mm2 tungsten tip emits a current of 15 mA at 3000 K and of only 0.8µA at 2000 K.

Practically, to obtain a permanent emission current, one must apply an external electric field : in the absence of such a field, the first electrons emitted into vacuum create a space charge, associated with an antagonistic electric field, which prevents any further emission.

Another way of calculating the emitted current consists in considering that in the TV tube, in the absence of applied electrical potential, an equilibrium sets up at temperature T between the tungsten electrons which try to escape the metal and those outside the metal that try to enter it.

The equilibrium between electrons in both phases is expressed through the equality of their chemical potentials. Now, outside the solid the electron concentration is very small, so that one deals with a classical gas which follows the Maxwell-Boltzmann statistics. The electron current toward the solid is calculated like for an ideal gas. When an electric field is applied, this current vanishes but the emission current, which is its opposite, remains.

Note that, in order to be rigorous, all these calculations should take into account the energy levels of the metal and its surface, which would be very

complicated! Anyhow, the above estimates qualitatively describe the e ect and lead to correct orders of magnitude.

On this example of the thermionic emission we have shown a practical application, in which electrons follow the high temperature limit of the Fermi-Dirac statistics.

both sides of µ compensate. Besides, we understood in §7.2.1 that, to maintain the same N when the temperature increases, µ gets closer to the origin, for a three-dimensional system for which ϕ (µ) > 0 when D(ε) is di erent from zero (ϕ(ε) √ε).

Let us write ∆ explicitly :

Here a symmetrical part is played by either the empty states below µ [the probability for a state to be empty is 1 − f (ε)], or the filled states above µ, all in small numbers if the temperature is low.

The integrals In are deduced from the Riemann ζ functions (see the section “A few useful formulae”). In particular at low temperature the principal term

of ∆ is equal to π2 (kB T )2ϕ (µ).

6

Let us return to the calculation of the specific heat Cv . For the internal energy of nonrelativistic particles, ϕ(ε) = ε · Kε1/2 = Kε3/2 for ε > 0, ϕ(ε) = 0 for ε < 0. Then