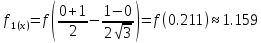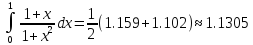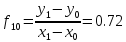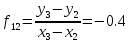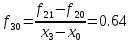Численные методы вар.15

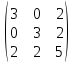
Дана матрица А=;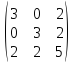

1)Решить систему уравнений Ах=b, где 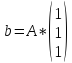способами:

- методом исключения Гаусса;

- методом Зейделя;

- методом простой итерации.

Перед началом вычислений рассчитаем b и запишем расширенную матрицу:

; Расширенная матрица

Метод Гаусса.

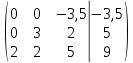
Ответ: (x=1, y=1, z=1).

Метод Зейделя. Предполагая, что a_ii ≠ 0 разрешим новое уравнение системы (1) относительно x₁, второе – относительно x₂,…, n-ое уравнение – относительно x_n. В результате получим: x₁=β₁ - α₁₂x₂ - α₁₃x₃ - ... - α_1nx_n x₂=β₂ - α₂₁x₁ - α₂₃x₃ - ... - α_2nx_n x_n=β_n - α_n1x_n - α_n3x₃ - ... - α_nn-1x_n-1 где β_i=b_i/a_ii; α_ij=a_ij/a_ii при i ≠ j; α_ii=0 Известно начальное приближение: x⁰=(x⁰₁, x⁰₂, ..., x⁰_n). Основная идея заключается в том, что при вычислении (k+1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k+1) - приближение неизвестных x₁, x₂, ..., x_n. Итерационная схема имеет вид: x^k+1₁=β₁ - ∑α_1jx^k_j x^k+1₂=β₂ - α₂₁x^k+1₁ - ∑α_2jx^k_j x^k+1_i=β_i - ∑α_ijx^k+1₁ - ∑α_2jx^k_j Прежде чем применять метод, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы.

Приведем к виду: x₁=1.667+0.67x₃ x₂=1.667+0.67x₃ x₃=1.8+0.4x₁+0.4x₂ Покажем вычисления на примере нескольких итераций. N=1 x₁=1.667 - 0 • 0 - 0 • 0.667=1.667 x₂=1.667 - 1.667 • 0 - 0 • 0.667=1.667 x₃=1.8 - 1.667 • 0.4 - 1.667 • 0.4=0.467 N=2 x₁=1.667 - 1.667 • 0 - 0.467 • 0.667=1.356 x₂=1.667 - 1.356 • 0 - 0.467 • 0.667=1.356 x₃=1.8 - 1.356 • 0.4 - 1.356 • 0.4=0.716 N=3 x₁=1.667 - 1.356 • 0 - 0.716 • 0.667=1.19 x₂=1.667 - 1.19 • 0 - 0.716 • 0.667=1.19 x₃=1.8 - 1.19 • 0.4 - 1.19 • 0.4=0.848

Остальные расчеты сведем в таблицу.

N	x1	x2	x3	e1	e2	e3
0	0	0	0
1	1.667	1.667	0.467	1.667	1.667	0.467
2	1.356	1.356	0.716	-0.311	-0.311	0.249
3	1.19	1.19	0.848	-0.166	-0.166	0.133
4	1.101	1.101	0.919	-0.0885	-0.0885	0.0708
5	1.054	1.054	0.957	-0.0472	-0.0472	0.0378
6	1.029	1.029	0.977	-0.0252	-0.0252	0.0201
7	1.015	1.015	0.988	-0.0134	-0.0134	0.0107
8	1.008	1.008	0.993	-0.00716	-0.00716	0.00573
9	1.004	1.004	0.997	-0.00382	-0.00382	0.00305
10	1.002	1.002	0.998	-0.00204	-0.00204	0.00163
11	1.001	1.001	0.999	-0.00109	-0.00109	0.000869
12	1.001	1.001	0.999	-0.000579	-0.000579	0.000463

Для оценки погрешности вычисляем коэффициент α: max[∑|α_ij|] = 0.4+0.4 = 0.8< 1 max[|x¹¹,x¹²|] = ρ(x¹¹, x¹²) = |0.999 - 0.999| = 0.000579 Вычисляем погрешность:

Метод простой итерации. Систему будем решать методом последовательных приближений. Пусть x⁰=β, тогда: x¹=b - a x⁰ x²=b - a x¹ .... x^k+1=b - a x^k Приведем к виду: x₁=1.667+0.67x₃ x₂=1.667+0.67x₃ x₃=1.8+0.4x₁+0.4x₂ Вычисления заканчиваются по критерию: где a=max ∑|r_ij| a = 0.4+0.4 = 0.8 Покажем вычисления на примере нескольких итераций. N=1 x₁=1.667 - 0 • 0 - 0 • 0.667=1.667 x₂=1.667 - 0 • 0 - 0 • 0.667=1.667 x₃=1.8 - 0 • 0.4 - 0 • 0.4=1.8 N=2 x₁=1.667 - 1.667 • 0 - 1.8 • 0.667=0.467 x₂=1.667 - 1.667 • 0 - 1.8 • 0.667=0.467 x₃=1.8 - 1.667 • 0.4 - 1.667 • 0.4=0.467 N=3 x₁=1.667 - 0.467 • 0 - 0.467 • 0.667=1.356 x₂=1.667 - 0.467 • 0 - 0.467 • 0.667=1.356 x₃=1.8 - 0.467 • 0.4 - 0.467 • 0.4=1.427 Остальные расчеты сведем в таблицу.

N	x1	x2	x3	e1	e2	e3
0	0	0	0
1	1.667	1.667	1.8	1.667	1.667	1.8
2	0.467	0.467	0.467	-1.2	-1.2	-1.333
3	1.356	1.356	1.427	0.889	0.889	0.96
4	0.716	0.716	0.716	-0.64	-0.64	-0.711
5	1.19	1.19	1.228	0.474	0.474	0.512
6	0.848	0.848	0.848	-0.341	-0.341	-0.379
7	1.101	1.101	1.121	0.253	0.253	0.273
8	0.919	0.919	0.919	-0.182	-0.182	-0.202
9	1.054	1.054	1.065	0.135	0.135	0.146
10	0.957	0.957	0.957	-0.0971	-0.0971	-0.108
11	1.029	1.029	1.035	0.0719	0.0719	0.0777
12	0.977	0.977	0.977	-0.0518	-0.0518	-0.0575
13	1.015	1.015	1.018	0.0384	0.0384	0.0414
14	0.988	0.988	0.988	-0.0276	-0.0276	-0.0307
15	1.008	1.008	1.01	0.0205	0.0205	0.0221
16	0.993	0.993	0.993	-0.0147	-0.0147	-0.0164
17	1.004	1.004	1.005	0.0109	0.0109	0.0118
18	0.997	0.997	0.997	-0.00786	-0.00786	-0.00873
19	1.002	1.002	1.003	0.00582	0.00582	0.00628
20	0.998	0.998	0.998	-0.00419	-0.00419	-0.00466
21	1.001	1.001	1.001	0.0031	0.0031	0.00335
22	0.999	0.999	0.999	-0.00223	-0.00223	-0.00248
23	1.001	1.001	1.001	0.00166	0.00166	0.00179
24	0.999	0.999	0.999	-0.00119	-0.00119	-0.00132
25	1	1	1	0.000883	0.000883	0.000953

Для оценки погрешности вычисляем коэффициент α: max[∑|α_ij|] = 0.4+0.4 = 0.8< 1 max[|x²⁴,x²⁵|] = ρ(x²⁴, x²⁵) = |1 - 0.999| = 0.000953 Вычисляем погрешность:

3. Для функции нужно численно найти производные первого и второго порядков в точках 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 и вычислить соответствующие погрешности. Найти также точку экстремума функции на (0,1). Обозначим эту точку экстремума x0.

Вычисление первой производной

По определению, первая производная гладкой функции f(x) в точке x вычисляется как

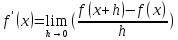
При вычислении первой производной функции f(x) на компьютере мы заменяем бесконечно ма- лое h → ∞ на малое, но конечное значение h:

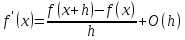
Аналитическое выражение первой производной имеет вид:

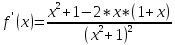
где O(h) — ошибка вычисления производной, естественно зависящая от h. Формула (1.1) называется разностной схемой для вычисления первой производной (более точно — правой разностной схемой или просто правой разностью). Аналогично, может быть записана левая разностная схема.

Где

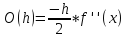
Вычисление второй производной

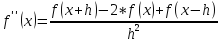
Аналитическое выражение второй производной имеет вид:

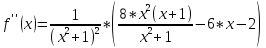
В целях экономии времени запишем вычисления в таблицу.

x	h	f’(x)	O(h)	f’’(x)
0.0	0.01	0.9999010098990191	0.01	-1.9998000199983323
0.2	0.01	0.5177532775471195	0.013086026399635867	-2.616954066798627
0.4	0.01	0.029797539600092106	0.010609291073844765	-2.1217726769195977
0.6	0.01	-0.3026933733324288	0.005979035212700997	-1.1958514917109753
0.8	0.01	-0.46098592502064734	0.0021945415765876855	-0.43897817751936685
1.0	0.1	-0.4977375565610853	0	-0.00499987500313103

Экстремумы функции на отрезке (0, 1) f_min = 0.5, f_max = 1.

4. Построить интерполяционный многочлен 3-го порядка в формах Лагранжа и Ньютона по точкам (0, p(0)), (х0, p(х0)), (1, p(1)). Построить графики исходной функции и интерполяционного многочлена по точкам x =b, где 0.0, 0.1, 0.2,...,0.9, 1.0, а также график относительной погрешности.

x	0	0.25	1
y	1	1.1765	1

Запишем формулу для интерполяционного многочлена в форме Лагранжа.

И подставим туда табличные значения, получим:

Полином Лагранжа

Составим таблицу разделенных разностей:

Запишем формулу для интерполяционного многочлена Ньютона и подставим туда полученные значения:

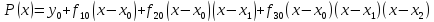
Построим графики исходной функции и полинома:

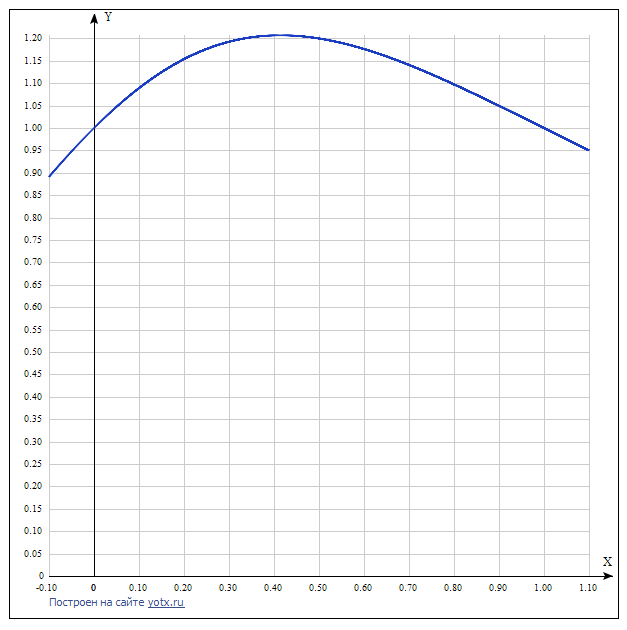
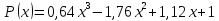
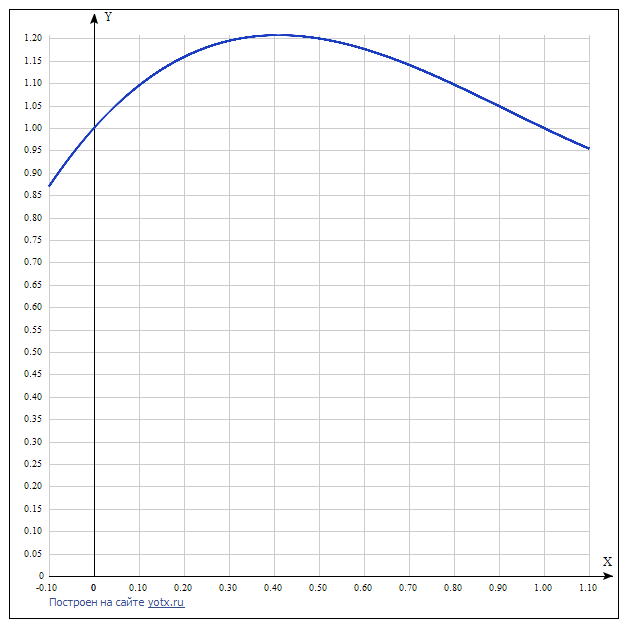
5. Снова рассмотрим многочлен p(x) на промежутке [0, 1], и вычислим точно и приближённо, методами трапеций и Гаусса, интеграл от этого многочлена.

Формула трапеций:

i	xi	yi
0	0	1
1	0.25	1.1765
2	0.5	1.2
3	0.75	1.12
4	1	1

Остаточный член квадратурной формулы:

Найдем максимальное значение второй производной функции на интервале [0;1]. y = 2/((x^2+1)^2)*((4*x^2*(x+1))/(x^2+1)-3*x-1) [0;1] Находим первую производную функции: y’ =  или Приравниваем ее к нулю: x₁ = 1.497 x₂ = 0.199 x₃ = -0.668 x₄ = -5.027 Вычисляем значения функции на концах отрезка f(1.497) = 0.269 f(0.199) = -2.617 f(-0.668) = 1.352 f(-5.027) = -0.0041 f(0) = -2.00000000000000 f(1) = 0 Ответ: f_min = -2.617, f_max = 0

Таким образом, I = 1.124 ± 0

Метод Гаусса.

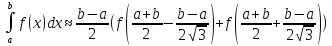
Найдём отдельно члены функции: