Методичка

бесконечное множество. Для проверки правильности рассуждений может быть использован метод доказательства от противного (закон противоречия – правило 6).

5.4 Метод резолюций в исчислении высказываний.

Метод резолюций является одним из методов доказательства от противного. Метод, предложенный Дж. Робинсоном, в настоящее время является теоретической базой большинства методов доказательства. Хотя общепринятые правила вывода, например, правило modus ponens, позволяют человеку проследить за каждым шагом процедуры доказательства, существует более сильное правило резолюций, которое трудно поддается восприятию, но эффективно реализуется на компьютере.

В настоящее время не существует эффективных критериев проверки выполнимости КНФ. Метод резолюций позволяет выявить невыполнимость множества дизъюнктов.

Этот метод использует тот факт, что если некоторая формула является невыполнимой, то наиболее сильное следствие этой формулы - константа False. Предложенный в 1965 году Дж. Робинсоном метод резолюций позволяет получить максимально сильное следствие множества формул с помощью систематической процедуры последовательного построения логических следствий формул, называемых резольвентами. Иными словами, метод резолюций обладает свойством полноты: для формулы Ф следствие False обязательно будет получено, если Ф — невыполнима.

Теорема 5.5 Пусть В — логическое следствие формулы А. Тогда А&В = А.

Доказательство теоремы легко проводится на основании определения понятия логического следствия. Действительно, пусть условие теоремы выполнено. Тогда А => В 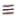True. Отсюда

A A & True A & ( A B) A( A B) A & A A & B False A & B A & B .

Определение. Резольвентой двух дизъюнктов 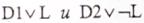называется дизъюнкт Dl v D2. Это записывается в виде

RESL(D1 v L, D2 v L) = D1 v D2.

Теорема 5.6 . Резольвента является логическим следствием порождающих ее дизъюнктов.

Доказательство. Пусть D 1vL и D 2v L,- два дизъюнкта. Тогда DlvD2их резольвента. Легко показать , что формула (D 1vL)&(D 2v L)=> (D 1vD 2) общезначима. Действительно, если имеются два высказывания (D 1vL) и

(D 2v L), которые имеют контрарные или инверсные (L, L ) литералы, то следствием из этих посылок является (D1 v D2 ). Проверим это утверждение: как известно А→В=¬А В, тогда (D 1vL)&(D 2v L)=> (Dl v D2)= ((D 1vL)&(D 2v L)) vD1v D2 = (D 1vL) v (D 2v L) vD1v D2 =1

Отсюда следует заключение теоремы.

71

Метод резолюций в доказательстве невыполнимости формулы Ф состоит в том, что формула Ф представляется в КНФ и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюций состоит в том, что он гарантирует получение для формулы Ф следствия False, если Ф невыполнима. Если же, перебрав все возможные резольвенты формулы Ф, мы не нашли пустую резольвенту, то Ф не является невыполнимой.

Метод резолюций есть фактически правило присоединения к рассуждению, в состав которого входят два утверждения А => В и А => С их следствия — утверждения В v С, что интуитивно совершенно очевидно. Действительно, первое утверждение гарантирует, что если А истинно, то В тоже истинно, а второе — что если А ложно, то истинно С. Очевидно, что в этом случае хотя бы одно из двух, В или С, всегда истинно. Добавление этого нового утверждения к исходному рассуждению не меняет его смысла.

На практике в общем случае метод резолюций не эффективен, мак как число переборов резольвент может быть очень большим. Оно экспоненциально зависит от числа дизъюнктов и содержащихся в них переменных. Метод успешно применяется только к одному классу дизъюнктов – хорновским дизъюнктам. Напомним, что дизъюнкт называется хорновским, если он содержит не более одной позитивной переменной,

например A v B vC, A vC, L vA,A.

5.5Вопросы для самопроверки.

1)Назовите основные понятия исчисления высказываний.

2)В чем заключается принцип дедукции?

3)Назовите основные схемы логически правильных рассуждений.

4)В чем заключается метод резолюции в логике высказываний ?

6)Придумать содержательное описание формулы:

(А→В) ↔ (А→С)

7)Дать определение резольвенте.

8)Дать определение хорновскому дизъюнкту.

9)В чем заключается закон контрапозиции?

10)В чем заключается логическое следование?

11)Что такое утверждающий модус – Modus Ponens?

12)Что такое отрицающий модус -Modus Tollens?

72

6.Исчисление предикатов и теории первого порядка.

6.1Исчисление предикатов. Основные понятия и определения.

Вданном курсе лекций описание формальной теории исчисления предикатов носит конспективный характер, в частности, многие сложные доказательства опущены. В то же время, основное внимание уделено прагматическим аспектам теории, которые могут принести большую пользу инженеру-программисту. Напомним еще раз наиболее важные аспекты исчисления предикатов.

Валгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности. Ни структура высказываний, ни, тем более, их содержание не рассматриваются. Очень часто возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать и структуру высказываний. Логика предикатов расчленяет элементарное высказывание на субъект (буквально – подлежащее) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).

Предикат - повествовательное предложение, содержащее предметные переменные, определенные на соответствующих множествах.

При замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т.е. принимает значение "истинно" или "ложно". Обозначение предиката, содержащего п переменных

(n-местного предиката): Р(х1, х2,..., хn), при этом предполагается, что х1 М1,

х2 М2, ..., хn Мn.

Другими словами, предикат (от лат. «сказуемое») Р(x1,x2,…,xn) – функция, переменные которой принимают значения из некоторого произвольного множества М или множеств, возможно, и бесконечных, а сама функция принимает только два значения: «истина» или «ложь»,0 или 1.

Переменные называются предметными или пропозициональными переменными. Вместо предметных переменных в предикат могут быть подставлены определенные значения из предметной области М. Таким образом, понятие предиката является расширением понятия «логическая функция». Предикат от n переменных называется n –местным предикатом. Можно считать, что высказывание – нульместный предикат. Например, в высказывании «семь - простое число», « семь – субъект», «простое число» - предикат. Высказывательная форма «х – простое число» является одноместным предикатом и выражает свойства субъекта. В общем случае для выражения «n» местного отношения используется «n» местный предикат. Множество истинности некоторого предиката – множество, в котором предикат принимает значение «1». Все формулы логики высказываний являются частными случаями логики предикатов. Все операции логики высказываний переносятся в логику предикатов, дополнительно в логике предикатов используются квантор всеобщности и квантор существования. Если переменная связана квантором, то она называется связанной, иначе – свободной. При определении формулы в исчислении предикатов используется

73

понятие «терм». Терм объединяет понятия переменных и функций, к которым применяются предикатные буквы. Символы функций и предикатов называют сигнатурой. Функции и предикаты иногда снабжаются верхним индексом для обозначения местности операции.

Спомощью логических связок (и скобок) предикаты могут объединяться

вразнообразные логические формулы - предикатные формулы. Исследование предикатных формул и способов установления их истинности является основным предметом логики предикатов. Логика предикатов вместе с входящей в нее логикой высказываний является основой логического языка математики. С ее помощью удается формализовать и точно исследовать основные методы построения математических теорий. Логика предикатов является важным средством построения развитых логических языков и формальных систем (формальных теорий).

Логика предикатов, как и логика высказываний, может быть построена в виде алгебры логики предикатов и исчисления предикатов. Здесь, как и в случае логики высказываний, для знакомства с основными понятиями логики предикатов воспользуемся языком алгебры, а не исчислений. Такой выбор обусловлен рядом причин:

• Исследование предикатных формул алгебры логики, выполнение их преобразований значительно проще, чем в исчислении предикатов.

• Ограничения в использовании аппарата алгебры обусловлены тем, что предметные области (множества, на которых определены предметные переменные предикатов) теоретически могут быть и бесконечными. В таких случаях стандартный метод проверки истинности предикатов и формул в целом, требующий подстановки всех возможных значений предметных переменных, не может быть осуществлен в строгом смысле (точнее, процедура вычисления истинности может быть бесконечной и не дать ответа за конечное время). Однако в практических ситуациях при описании реальных систем, процессов, явлений в качестве предметных областей, как правило, используются конечные множества. Поэтому проблема бесконечности в значительной степени теряет свою актуальность.

n - местный предикат - это функция Р(х1, х2,..., хn) от п переменных, принимающих значения из некоторых заданных предметных областей, так

что х1 М1, х2 М2, ., хn Мn, а функция Р принимает два логических значения - "истинно" или "ложно" (обозначения: {И, Л}, {1, 0}). Таким образом, предикат Р(х1,х2,...,хn) является функцией типа Р: М1 x М2 x ... x Мn →

B, где множества М1, М2, ..., Мn называются предметными областями

предиката; х1, х2,..., хn - предметными переменными предиката; В - двоичное (бинарное) множество: В = {И, Л} или {1,0}. Если предикатные переменные принимают значения на одном множестве, то Р: Мn→В.

Соответствия между предикатами, отношениями и функциями:

1. Для любых М и п существует взаимно однозначное соответствие между n -местными отношениями R M n и п - местными предикатами Р(х1,

х2,..., хn), Р: Мn→В:

74

• каждому n - местному отношению R соответствует предикат Р(х1, х2,...,

хn) такой, что Р(a1, a2,..., an) = 1, если и только если (a1, a2,..., an) R;

• всякий предикат Р(х1, х2,..., хn) определяет отношение R такое, что (a1,

a2,..., an) R, если и только если Р(a1, a2,..., an) = 1.

При этом R задает область истинности предиката Р.

2. Всякой функции f(х1, х2,..., хn), f: Мn → М, соответствует предикат Р(х1, х2,..., хn, хn+1), Р: Мn+1→В, такой, что Р(a1, a2,..., an, an+1 ) = 1, если и только если f(a1, aх2,..., an) = an+1.

Понятие предиката шире понятия функции, поэтому обратное соответствие (от (n+1)-местного предиката к n - местной функции) возможно не всегда, а только для таких предикатов Р’ для которых выполняется условие, связанное с требованием однозначности функции.

6.2 Синтаксис и семантика языка логики предикатов.

Определим синтаксис логики предикатов первого порядка.

Классическое исчисление предикатов (первого порядка) - это формальная теория, в которой определены следующие компоненты:

1. Алфавит

<переменная><формула>|< переменная >< формула >

75

При этом должны быть выполнены следующие контекстные условия: в терме f(t1, ..., tn) функтор f должен быть n-местным. В атоме (или атомарной формуле) P(t1, ..., tn) предикат P должен быть n – местным.

Другими словами синтаксис логики предикатов можно определить так:

Алфавит

1.Предметные переменные x,y,z,… и логические константы а,b,c,…

2.Функциональные константы или имена функции.

3.Предикатные константы или имена предикатов.

4.Логические операторы.

5.Символы кванторов.

6.Служебные символы.

Понятие формулы определяется в три этапа:

А. Термы

1.Всякая переменная или константа есть терм.

2.Если 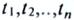– термы и – функциональная n- местная константа , то

– терм. Здесь верхний индекс определяет количество аргументов. 3. Никакие другие выражения не являются термами.

В. Атомы

1.Если 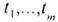- термы и 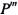- m-местная предикатная константа , то 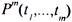- атом . При m=0 предикат Р(0 ) обращается в высказывание Р. Атомом является также равенство , т.е. выражение типа (s=t), где s и t – термы. Для равенства характерно то же, что и для предикатной формы, т. е. о нем можно сказать, что оно истинно или ложно. Можно сказать, что атом – это предикатная форма или равенство.

2.Никаких других атомов нет.

С. Формулы

Формулы (или правильно построенные формулы – ППФ) определяются следующим образом:

1.Всякий атом есть формула.

2.Если А – формула, то – А – формула.

3.Если А и В – формулы , а х – свободная переменная , то

- формулы.

4. Никаких других формул в исчислении предикатов нет.

В пределах формализма логики предикатов первого порядка запрещено использование предикатов в качестве термов, навешивания кванторов на предикатный символ.

Предикат 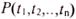служит для выражения свойства объекта (при n=1) и отношений между объектами (при п 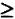2). Атомарная формула

76

истинна в некотором "мире" (М), если между объектами в М имеет отношение, соответствующее Р.

Связывание свободной переменной происходит либо квантификацией (взятием квантора по этой переменной) либо присвоением значения. Вхождения переменных в атомарную формулу называются свободными. Свободные вхождения переменных в формулах А и В остаются свободными и в формулах А и А В. Вхождения переменной x в формулы x A и x A называются связанными. Вхождения других переменных (отличных от x), которые были свободными в формуле А, остаются свободными. Формула, не содержащая свободных вхождений переменных, называется замкнутой. Формулы вида A и A, где A - атом, называются литеральными формулами

(или литералами).

В формулах x A(х) и x A(х) подформула A(х) называется областью действия квантора по x.

При этом необходимо, чтобы выполнялись следующие условия:

1.В формуле свободные и связанные переменные обозначаются разными буквами.

2.Если какой либо квантор находится в области действия другого квантора, то переменные связанные этими кванторами обозначаются разными буквами. Нарушение этих двух условий называется коллизией переменных. Например, выражение x(F(x) xG(xy)) не является

формулой, так как нарушено 2 условие.

Обычно связки и кванторы упорядочивают по приоритету следующим образом: , , , , , . Лишние скобки при этом опускают.

Терм t называется свободным для переменной x в формуле A, если никакое свободное вхождение переменной x в формулу A не лежит в области действия никакого квантора, входящего в терм t. В частности, терм t свободен для любой переменной по формуле A, если никакая переменная терма не является связанной переменной формулы A.

3. Система аксиом исчисления предикатов.

Эти система состоит из двух групп, из которых первая – это аксиомы формализованного исчисления высказываний. Вторая группа аксиом (схем аксиом) – это аксиомы, связанные с использованием кванторов (аксиомы Бернайса).

I.1. A→(B→A);

I.2. (А→(В→С))→((А→В)→(А→С)); I.3 (¬В→¬А)→((¬В→А)→В ).

II.1 xF(x) F(y)

II.2 F(y) x F(x), где F(x) – любая формула, содержащая свободные вхождения х, причем ни одно из них не находится в области действия квантора по у (если таковой имеется). Формула F(y) получена из F(x) заменой всех свободных вхождений х на у.

77

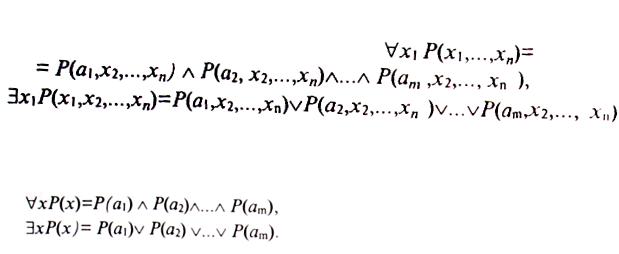
Если предметные переменные определены на конечной области, то операцию навешивания кванторов можно выразить через операции конъюнкции и

дизъюнкции соответственно. Пусть 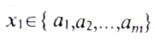, тогда

в частном случае

Говорят, что квантор связывает соответствующую переменную. Предикат (формула) называется замкнутым, если связаны все его переменные (если нет свободных, т.е. несвязанных переменных).

Формула называется истинной в данной интерпретации I, если она выполнена на любом наборе s элементов M. Формула называется ложной в данной интерпретации I, если она не выполнена ни на одном наборе s элементов M.

Интерпретация называется моделью множества формул , если все формулы из истинны в данной интерпретации.

Всякая замкнутая формула истинна или ложна в данной интерпретации. Открытая (то есть не замкнутая) формула A(x, y, z, ...) истинна в данной интерпретации тогда и только тогда, когда ее замыкание x y z ... A(x, y, z,

...) истинно в данной интерпретации. Это обстоятельство объясняет, почему собственные аксиомы прикладных теорий обычно пишутся в открытой форме.

Формула (исчисления предикатов) общезначима, если она истинна в любой интерпретации.

Логическое следование и логическая эквивалентность.

Формула В является логическим следствием формулы А (обозначение: А В), если формула В выполнена на любом наборе в любой интерпретации, на котором выполнена формула А. Формулы А и В логически эквивалентны (обозначение: А = В), если они являются логическим следствием друг друга. Имеют место следующие логические следования и эквивалентности:

79

6. Закон выведения нульместного предиката С из области действия квантора

x x (A(x) & C) = x A(x) & C; x (A(x) C) = x A(x) C; 7. Закон введения нульместного предиката С в область действия квантора

C x A(x) = x (C A(x)); C x A(x) = x (C A(x)); 8. Закон введения нульместного предиката С в область действия квантора

x A(x) C x (A(x) C); x A(x) C x (A(x) C).

где формула С не содержит никаких вхождений переменной x.

Для всякой формулы А существует логически эквивалентная ей формула А’ в

предваренной форме:

A': Q1 x1...Qn xn A(x1 ,..., xn ) ,

где Q1 ,...Qn - некоторые кванторы, а A - бескванторная формула.

6.3Метод резолюций в логике предикатов.

По существу метод (принцип) резолюции был обоснован Ж.Эрбраном в 1930г. Первым реализовал на ЭВМ идеи Эрбрана Дж. Робинсон в 1963г. Метод резолюции - один из методов доказательства от противного. Основная идея метода заключается в попытке вывести из множества дизъюнктов S пустой дизъюнкт, для которого нет интерпретаций и который, тем самым, гарантирует невыполнимость множества дизъюнктов. Процесс вывода пустого дизъюнкта может быть представлен процессом сведения числа вершин замкнутого дерева к единственной неблагоприятной вершине. Мнемоническое правило вывода можно сформулировать, следующим образом: если пара исходных дизъюнктов множества S содержит контрарные литералы (X и ⌐Х), то новый дизъюнкт формируется из оставшихся частей дизъюнктов, не содержащих эти контрарные литералы. Этот вновь сформированный дизъюнкт называется резольвентой исходных дизъюнктов. Общезначимость правила резолюций выражается следующей леммой.

Лемма 1. Пусть S1 и S2 — дизъюнкты нормальной формы S, I —литера. Если

, то дизъюнкт является логическим следствием нормальной формы S.

Если в процессе вывода новых дизъюнктов мы получаем два однолитерных дизъюнкта, образующих контрарную пару, то резольвентой этих двух

80