Лабораторная работа 1 по ВМ

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

ОТЧЁТ

по лабораторной работе №1

«Методы решения нелинейных уравнений»

Отчёт подготовил:

студент БСТ1401 Балашов И.М.

Москва 2015 г.

Нелинейное уравнение: e^x-4e^(-x)-1=0

Точность

На компьютере: метод итерации.

Вручную: метод хорд.

Отделение корней

График функции:

x:=0.7, 0.8…1.7

Как видно только на промежутке х=[0.8;1] значение f(x) меняет знак, следовательно уравнение имеет хотя бы один корень. Из таблицы видно, что первая и вторая производные f'(x) и f''(x) знакопостоянны и непрерывны на всем отрезке.

0.7	-0.9726	4.0001	0.0274
0.8	-0.5718	4.0229	0.4282
0.9	-0.1667	4.0859	0.8333
1	0.2468	4.1898	1.2468
1.1	0.6727	4.3357	1.6727
1.2	1.1153	4.5249	2.1153
1.3	1.5792	4.7594	2.5792
1.4	2.0688	5.0416	3.0688
1.5	2.5892	5.3742	3.5892
1.6	3.1454	5.7606	4.1454
1.7	3.7432	6.2047	4.7432

Метод хорд (ручной расчёт):

Для сходимости процесса необходимо, чтобы была знакопостоянна на , что и было доказано ранее.

Рекуррентная формула метода хорд:

где - неподвижная точка.

За неподвижную точку в методе хорд выбирают тот конец отрезка [a;b], для которого выполняется условие f (x)∙ f¢¢ (x) > 0. В данном случае, исходя из таблицы, это будет точка b=1.7.

Тогда рекуррентная формула будет иметь вид:

Ручной расчет трех итераций:

= 1.7

= 0,9062428

f(

n	Xк	f(xк)
0	0.7	-0.9726
1	0,9062428	-
2		-
3		-

После трех итераций приближение к корню .

Оценка погрешности результатов:

Метод итераций (машинный рассчет):

Приведем уравнение 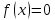к виду , тогда рекуррентная формула .

Для сходимости процесса итерации необходимо, чтобы при

Следовательно, сходимость не обеспечена. Тогда построим функцию: , где , так как , где

возьмём , тогда

Рекуррентная формула имеет вид:

Схема алгоритма метода итераций:

Код программы:

#include <iostream>

#include <conio.h>

#include <math.h>

using namespace std;

double f(double x)

{

return exp(x)-4*exp(-x)-1; //исходное уравнение

}

double fi(double x)

{

return x - 0.05*f(x); //итерирующая функция

}

void rasschet(double x, double E)

{

double t = x;

double f1, f2;

int n = 0; //кол-во итераций

do

{

x = t;

t = fi(x); //получение очередного приближения к корню

f1 = f(x);

f2 = f(t);

n = n + 1;

cout << "\nитерация: " << n << " корень: " << x << " f(x):" << f(x);

} while (!((abs(x - t)<E) && (abs(f1 - f2)<E)));

cout << "\nРезультаты:";

cout << "\nитерация:" << n << " корень:" << x << " f(x):" << f(x);

}

void main()

{

setlocale(LC_ALL, "Russian");

do{

cout << "Программа расчёта корня нелинейного уравнения методом итераций\n\n";

double x, E;

cout << "Введите х: ";

cin >> x; // начальное приближение

cout << "Введите точность Е: ";

cin >> E; //точность вычислений

rasschet(x, E);

} while (getch() == 'y');

}

Результаты расчёта на ПК:

E	n	x	f(x)
0.001	1	0.939712	-0.00371716
0.0001	10	0.940501	-0,000465506
0.00001	11	0.940602	-0.0000461622

Зависимость числа итераций от точности в логарифмическом масштабе:

ε	0.001	0.0001	0.00001
n	1	10	11