Добавил:

Tototo Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

Объектно ориентированное программирование

Файл:

Мат. программирование - Лк1

.pdf

Скачиваний:

Добавлен:

07.09.2016

Размер:

328.59 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Линейное программирование

1.1 Примеры задач линейного программирования

1.1.1 Задача планирования выпуска продукции (планирование производства)

Машиностроительное предприятие для изготовления четырех видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. Кроме того, сборка изделий требует выполнения сборочно-наладочных работ. Нормы затрат всех видов ресурсов на изготовление каждого из изделий приведены в таблице (см. табл. 1.1). В этой же таблице указан имеющийся фонд каждого из ресурсов и прибыль от реализации одного изделия каждого вида.

Таблица 1.1− Нормы затрат на изготовление одного изделия

	Нормы затрат на				Общий
	Нормы затрат на				объем
Ресурсы	изготовление одного				объем
Ресурсы					ресур-
					ресур-
		изделия			сов
					сов

1	2	3	4	5	6
Производительность
оборудования (чел.-час)
Токарного	550	-	620	-	64270

Фрезерного	40	30	20	20	4800

Сверлильного	86	110	150	52	22360

Расточного	160	92	158	128	26240

Шлифовального	-	158	30	50	7900

Комплект изделия (шт.)	3	4	3	3	520

Сборочно-наладочные	4,5	4,5	4,5	4,5	720
работы (чел.-час.)

Продолжение таблицы 1.1

	Нормы затрат на				Общий
	Нормы затрат на				объем
Ресурсы	изготовление одного				объем
Ресурсы					ресур-
					ресур-
		изделия			сов
					сов

1	2	3	4	5	6
Прибыль от реализации	315	278	573	370
одного изделия (руб.)

Надо составить такой план выпуска продукции, чтобы получить максимальную прибыль. Построим математическую модель данной задачи. Пусть x1 – планируемое количество изделий 1-го типа, x2 , x3 , x4 – планируемое количество изделий 2-го, 3-го, 4-го типов соответственно.

Тогда

f=315x1 +278x2 +573x3 +370x4 (1.1)

прибыль предприятия. Так как нам надо получить как можно большую прибыль, то будем искать наибольшее (максимальное) значение функции f. Общие объемы ресурсов накладывают на нашу задачу ограничения

550x1 + 620x2 ≤ 64270
40x1 + 30x2 + 20x3 + 20x4 ≤ 4800
86x1 + 110x2 +150x3	+ 52x4 ≤ 22360
160x1 + 92x2 + 158x	3 + 128x4 ≤ 26240	(1.2)
158x2 + 30x3 + 50x4 ≤ 7900

3x1 + 4x2 + 3x3 + 3x4 ≤ 520

4.5x1 + 4.5x2 + 4.5x3 + 4.5x4 ≤ 720.

Так как целевая функция и ограничения являются линейными, то это задача линейного программирования.

1.1.2 Задача планирования капитальных вложений

Для электроснабжения трех стройплощадок используются две трансформаторные подстанции. Первая стройплощадка потребляет 130 кВт, а вторая и третья по 140 кВт. Мощность первой ТП – 250 кВт, а второй 160 кВт. Расстояние от первой ТП – 600, 400, 200 м, до первой, второй и третьей площадки соответственно. От второй ТП: − 500, 300 и 200 м соответственно. Требуется составить схему электроснабжения с минимальными капитальными вложениями.

Капитальные вложения для устройства линий рассчитываются по следующей формуле:

3 2

∑ ∑

= α ∑ ∑ S

(1.3)

j =1i=1

ij ij

j =1 i=1 3U j

где:

Sij – мощность,

потребляемая j-ой площадкой от i-ой

ТП,

кВт;

lij –

расстояние от j-ой площадки до i-ой ТП, м.;

α –

постоянный множитель.

Итак, нам надо минимизировать функцию

f=α(6S11 +4S12 +2S1 3 +5S21 +3S2 2 +2S2 3 ),

(1.4)

при ограничениях:

S11 + S21 =130;

S12 + S22 =140;

S13 + S23 =140;

(1.5)

S11 + S12 + S13 =250;

S21 + S22 + S23 =160 .

Как и в предыдущем примере имеем задачу линейного программирования.

1.2 Основные определения

ОПРЕДЕЛЕНИЕ 1.1. Задача, состоящая в нахождении наибольшего (наименьшего) значения функции

f(x)=с1 x1 +c2 x2 + … + cn хn

(1.6)

на множестве точек xT =(x1 ,…, xn ), удовлетворяющих системе ограничений вида:

a1 1 x1 + a1 2 x2 +…+ a1n xn < R1	> b1
a21 x1 + a22 x2 +…+ a2n xn < R2	> b2
. . . . . . . . . .	(1.7)

am1 x1 + am2 x2 +…+ amn xn < Rm > bm

называется задачей линейного программирования общего вида.

Здесь:

f( x )=с1 x1 + c2 x2 + … +			cn xn – целевая функция;
Ri, i =		– операции	отношения =, ≥,≤;
	1,m

ci , i = 1, n ; aij , i = 1, m, j = 1,n ; bi , i = 1, m – заданные кон-

станты.

ОПРЕДЕЛЕНИЕ 1.2. Всякую точку xT =(x1 ,…, xn ), компоненты которой удовлетворяют всем ограничениям системы (1.7), будем называть допустимой точкой или допустимым решением задачи, или допустимым планом задачи.

Задача линейного программирования состоит, таким

образом, в нахождении такой допустимой точки x(0) (такого допустимого плана) среди множества допустимых точек, при которой целевая функция принимает max (min) значение. Допустимое решение x(0) = (x1 (0) ,…, xn ( 0 ) )T , доставляющее целевой функции оптимальное значение (оптимум), будет называться оптимальным решением или оптимальным планом задачи. В дальнейшем будем говорить, к примеру, только о нахождении max целевой функции.

Задачу линейного программирования, представлен-

ную в виде:

f = с1 x1	+ c2 x2 + … + cn xn → max (min)
a11 x1 + … + a1n xn = b1
a21 x1 + … + a2n xn = b2
.	. . . . . .	(1.8)
am1 x1 + … + amn xn = bm

xi	≥ 0, i = 1,n ;

будем считать канонической задачей линейного программирования.

Введением дополнительных переменных, мы можем любое ограничение вида неравенства свести к ограничениям – равенствам. Если не на все переменные наложено требование неотрицательности (слабые ограничения), то такие переменные можно заменить разностью двух новых переменных, каждая из которых неотрицательна. Проиллюстрируем сказанное на примере.

Пример 1.1. Привести к каноническому виду задачу:

f= x1 –2 x1 +x3 → max x1 + 2x2 + 3x3 ≤ 5

2x1 +3x2	– 4 x3 = 3	(1.9)
– x1 + x2 – x3 ≥ 2
x1 ³ 0, x2	³ 0.

Введем две дополнительные неотрицательные переменные x4 и x5 в первом и третьем ограничениях, так, чтобы получить ограничения – равенства. Кроме того, переменную x3 представим в виде:

x3 = x3

׳ – x3

״,

(1.10)

где: x3 ׳ ³ 0, x3 ״ ³ 0.

Получим:


f = x1 – 2 x1 + x3		׳	– x3	״	→ max,
x1 + 2x2 + 3(x3 ׳ – x3 ״) + x4 = 5
2x1 +	3x2 – 4( x3		׳ – x3		״) = 3	(1.11)
– x1 –	x2 – ( x3 ׳ – x3 ״) – x5 = 2

x1 ³ 0, x2 ³ 0, x3 ׳ ³0, x3 ״ ³0, x4 0, x5 ³ 0,

а это уже задача в канонической форме.

Введя в рассмотрение векторы

c =(c1, c2, … cn), x = (x1, … , xn)T, b = (b1,…, bm)T, A=	a11 …	a1n
c =(c1, c2, … cn), x = (x1, … , xn)T, b = (b1,…, bm)T, A=	a21 …	a2n
	. . . . . . .
	am1 …	amn

можем переписать задачу (1.6),(1.7) линейного программирования в форме:

f = c · x → max(min)	(1.12)
Ax = b	(1.13)
	(1.13)
x ³ 0 .

1.3 Геометрическая интерпретация двумерной задачи линейного программирования и ее решение

Рассмотрим двумерную задачу:

f = c1 x1	+ c2 x2 → max(min),		(1.14)
a1 1 x1	+ a12 x2 < R1	> b1
a2 1 x1	+ a22 x2 < R2	> b2
. . . . .			(1.15)
am1 x1 + am2 x2 < Rm > bm .
Каждое из ограничений ai1 x1		+ai2 x2 < Ri > bi определяет
в плоскости, с системой координат x1 o x2			множество то-

чек, лежащих по одну сторону от прямой ai1 x1 +ai2 x2 =bi (т.е. полуплоскость). Множество всех точек плоскости, координаты которых удовлетворяют всем ограничениям, т.е. принадлежат сразу всем полуплоскостям, определяемым отдельными ограничениями, будет представлять собой допустимое множество. Очевидно, что, если множество не пусто, то это будет некоторый многоугольник (возможно и неограниченный, возможно вырождающийся в отрезок, точку). Многоугольник будет выпуклым, что легко показать, т.е. любые две его точки можно соеди-

нить отрезком, точки которого принадлежат допустимому множеству.

ОПРЕДЕЛЕНИЕ 1.3. Множество D-точек n-мерного

евклидова пространства будем называть выпуклым, если

для любых x( 1 ) =(x1 ( 1 ) ,…, xn ( 1 ) )T и x(2) =(x1 (2) ,…, xn ( 2) )T из

множества D и любых α ≥0, β≥0 таких, что α+β=1, точка x=αx(1 ) +βx(2) также принадлежит D.

ОПРЕДЕЛЕНИЕ 1.4. Вершиной выпуклого множества

в Rn назовем такую точку, которую нельзя представить в виде x=αx(1) +βx(2) , α>0, β>0, α+β=1, ни при каких x( 1) ,x(2 ) .

Проиллюстрируем вышесказанное примерами. Примеры: изобразить множество точек, удовлетво-

ряющих системе неравенств.

1) 2x1 – 3 x2 £ 2	2) – x1 + x2 £ 1
3x1 – x2 £ 1	x1 – 2 x2 £ 1

	- x +		1 x £1			x1 ³ 0
		1	2	2
	x1	³ 0				x2 ³ 0
	x2	³ 0
3)	3 x + x ³ 3				4)	3x -	1 x £ 3
	4	1	2			2	2	1
	x1 + x2 £ 1					x1 + x2 ³1
	x2 £1					x1 + x2 £1
						x2 –	x1 ³–1

Построив допустимые множества, убедимся в вышесказанном.

Рассмотрим теперь геометрическую интерпретацию решения задачи линейного программирования. Пусть допустимая область задачи (1.14)−(1.15) оказалась непустой (в соответствии с рисунком 1.1).

f =amin

(x1(0) , x2(0) ) – точка максимума

	f=amах
Точка
минимума
n= grad f	f = c1x1 + c2x2	= a
	х1

Рисунок 1.1 - Геометрическая интерпретация задачи линейного программирования

Мы хотим найти те точки допустимой области, координаты которых доставляют целевой функции наибольшее значение. Построим линию уровня целевой функции f=c1 x1 +c2 x2 =a . Получим множество точек, в точках которого f принимает одно и тоже значение a . Перемещая линию уровня в направлении вектора grad f=(c1 , c2 )=n, нормального к линии уровня, будем получать в пересечении этой линии с допустимой областью точки, в которых целевая функция принимает новое значение, большее чем значение на предшествующих линиях уровня.

Пересечение допустимой области с линией уровня в том ее положении, когда дальнейшее перемещение дает пустое множество, и будет множеством точек максимума задачи линейного программирования. Перемещая линию уровня в направлении противоположном вектору n, аналогичным образом найдем точки минимума.

Пример 1.2.

f= x2 – 2 x1 → max

–x1 + x2 £ 1 x1 – 2 x2 £ 1 x1 ³ 0, x2 ³ 0

x2	f = –2 x1 + x2 = 0

f =1

n (–2,1)

–2

–1

0.5

Рисунок 1.2 - Геометрическая интерпретация задачи линейного программирования

Точка максимума: x=(0, 1)T ;

fm a x =f(0, 1)=1.

Легко представить, что задача имеет бесчисленное множество оптимальных решений, а может их не иметь вовсе, как например:

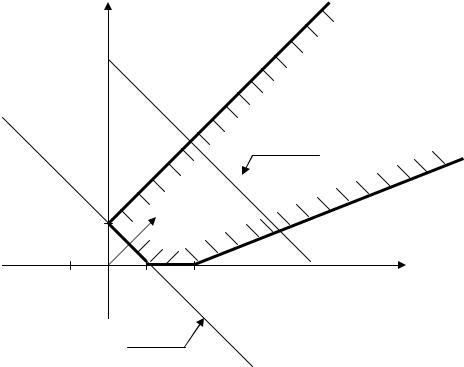
f = x1 + x2 → min(max); x1 + x2 ³ 1

– x1 + x2 £ 1 x1 – 2 x2 £ 2 x1 ³ 0, x2 ³ 0.

Целевая функция достигает минимального значения в точках отрезка x1 +x2 =1, между точками (0, 1) и (1, 0), а максимального значения функция не достигает (не ограничена в допустимой области).

f=K

1 n(1,1)

–1	1		2	x1
		–1

f =1

Рисунок 1.3 − Геометрическая интерпретация задачи линейного программирования

1.3.1 Свойства задачи линейного программирования

Рассмотренные примеры позволяют сформулировать основные свойства задачи линейного программирования.

Свойство 1. Допустимая область задачи линейного программирования выпукла, если она не пуста.

Свойство 2. Если допустимая область имеет вершины и задача линейного программирования имеет решение, то оно достигается по крайней мере в одной из вершин.

Свойство 3. Множество решений задачи линейного программирования выпукло.

Свойство 4. Если допустимая область ограничена, то любая задача линейного программирования имеет оптимальное решение.

Свойство 5. Необходимым и достаточным условием существования решения задачи линейного программирования на максимум (минимум) является ограниченность

1 / 51 2 3 4 5 > Следующая >>>