
Разбор лекций
.pdf
Если во множестве Х– несколькоэлементов,тосмотримдлину каждогои выбираем максимальную.
Опр. Граф Эйлера ГS полугруппы (или группы) G,порожденной системой образующих элементовS,построенный посистеме образующихS– этоориентированный граф с множествомвершин Gи множествомдуг,которые помечены элементами множестваS.
Другими словами:впервуюочередь,имеем<S>=G,т.к. группа Gпорождена Sпоусловию. Граф Эйлера нагляднонампоказывает,чтобудет сэлементомg,если к нему применить операциюсэлементомs. Например,перемножить.
Вот смотрите – такэтовыглядит на бумаге:g*s=g’.
А так– ввиде графа
Замечание:изкаждой вершины графа Эйлера исходит sдуг.
Почему так?Смотрите.
Было:S={s1, s2, s3}– всегоsштук;G={g1,g2…}– обычная группа
Стало:<S>= G={s1, s2, s3и все их произведения}.
Таквот, к любому элементуg можноприменить операциюслюбымизsэлементов. Например,умножить,если группа задана относительноумножения. Уже,наверное,не стоит повторять,чтокакэлемент g,таки все элементы s1,s2…входят в группу <S>.А группа подразумевает замкнутость – можемумножить любые 2элементаи получимэлемент изэтой группы. Тоесть может смелоумножить любой взятый произвольноg на любое из{s1, s2…}.
В виде графа этовыглядит вот так,какраз в видеs исходящих стрелочек. Напомним,этот граф показывает,вочтопереходит элемент,если кнему применить операциюсs1,s2…
Опр. Ориентированный граф называется псевдосимметрическимпорядка р,если для любой еговершины x полустепень исхода вершины x равна полустепени захода вершины x и равнаp:
Pисх(х) = рзах(х) = р
Другими словами:простоопределение,ничегобольшего.
Свойстваграфов Кэлли.
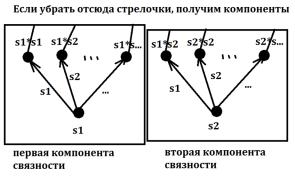
1.Граф,полученный изграфаSзаменой дуг наребра,содержит не более |S|компонент связности.
Другими словами:для начала напомнимопределение:Опр.Компоненты связности неориентированногографа– этомаксимальноемножество вершин, гделюбаявершина достижимаизлюбойдругой.
Тоесть если изориентированногографа сделатьнеориентированный (убрать стрелочки, или,по-научному,заменить дугина ребра),тополучимколичествокомпонент связности, не превышающееколичества вершин в исходномграфе.
Ну действительно,предельный случай будет вот таким:
Тоесть изs1 никакнельзя получить s2и т.д.
Всеготаких компонент связности-|S|- количество вершин в исходномграфе.
2.Любая вершинадостижима хотя бы из1вершинымножестваS.
Другими словами:помните «толюбой элемент изGможнопредставить какконечное произведение элементовизS»?Здесь пополной аналогии. Например,если были у нас заданы элементы s1,s2, s3,то элемент s1*s2достижимуже издвух вершин:изs1и s2 (рисуноквыше).
Утв. ЕслиSпорождает группу,тоГS – псевдосимметричный граф,порядоккоторого (количествовершин) равен мощностиS.
Другими словами:ключевое словоздесь– порождает ГРУППУ. Настоящуюгруппу,в которой выполняется все,чтодолжновыполнятьсявгруппе.
Свойство. ЕслиSпорождает группу,тоPисх(х) = рзах(х) =|S|для любогоg из <S>.
Доказательство. Чуть раньше мы уже разобрались,почему изкаждой вершины исходитsдуг:

Осталось доказать,чтов одну вершину не может заходить 2дуги содинаковыми метками. Делается этосовсемпросто,наоснове одногопреобразования.
Предположим,чтов вершину g заходят 2дуги содинаковыми метками.
Получили,чтов одну вершинуне могут заходить 2дуги с1меткой. Поэтому полустепень захода любойвершины не превосходит |S|.
Криптограф,всегда шифрующий методомпростой замены,на этомостановится. Настоящий же криптоаналитик,который признает толькоAES, пойдет еще дальше и докажет,что полустепень заходаравна|S|. И мы,конечно,последуемза ним.
На самомделезашифровать в умеAESнамногопроще,чемпростой заменойв этом доказательстве нет ничегосложного. Мы уже знаем,чтоизкаждой вершины исходитs стрелочек,и в каждуювершину заходит неболее одной стрелочки скаждой изметок. Нам предлагается доказать,чтополустепень заходалюбой вершины равна|S|. Действительно,на каждуюизвершин можноподействовать каким-тоэлементомизS,поэтому изкаждой вершины выходит sстрелочек. С этиммы уже разобрались раньше. А теперь представим,чтов какую-товершину такая стрелочкане зашла. Стрелочекосталось s, а вершин сталоs-1. Тогда она зайдет в какую-тодругуювершину. Новнее уже заходила стрелочка стакой же меткой– вторая такая же зайти не может – противоречие. Тоесть если хотя бы 1стрелочка не войдет какую-товершину,токоличествотаких стрелочекбудет уже больше,чемколичествовершин, и ей придется зайти второй разв другуювершину,чтоневозможно.
Еще раз другими словами:из каждой вершины выходитsстрелочек,причемзаходить в каждуювершину стрелкасодной меткой может только1раз. Поэтому вкаждуювершину должнои заходить sстрелочек,иначе возникнет несоответствие количества стрелок количеству вершин.
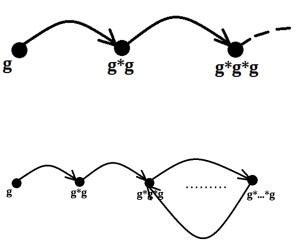
Давайте разберемся,почемуG=<g> называется циклической. Возьмемединственный элемент g и зададимоперацию– шифрование умножение. Какие элементы можнополучить изg, используя умножение?Правильно:g,g*g,g*g*g (нуточнее g,g2,g3 и т.д. – мы же будущие криптоаналитики).
Если бы Gбыла бесконечна,былобы совсемпонятно:
Нодавайте решим,чтоG– конечна. Тоесть количествоэлементов вней ограничено. Тогда, ввиду такой ограниченности,на каком-тошаге мы получимто,чтоуже было:
Скажете,невозможно,чтобы g99=g3?На первый взгляд да,номы же криптографы!Вспомните, например,прокольцовычетов помодулю. Где-томы их уже разбирали.
Теперь,счувствомполногопонимания циклических полугрупп,можноперейти ких изучению.
Опр. Пусть g – элемент g изполугруппы G.
Тогда если в ряду элементовg,g2,g3…gn не встречаются одинаковые элементы,тополугруппа, порожденная элементомg,и ее порядокназываются бесконечными.
Если в ряду g,g2,g3… есть одинаковые (аеслиGконечна,тоони неизбежны,т.к. множество, порожденное элементомg,всегда является подмножествомG),тосделаемвот что. Обозначимt– наименьшее натуральное число,такое чтопри некоторомd<t:gd=gt (тоесть t– наименьший номервпоследовательностиg,g2,g3,с которогоначинают появляться повторения).
Таккак d<t, можнозаписать:gd=gd+n. Такая форма называется определяющимсоотношением конечной циклической полугруппы. Можнои вот такзаписать:gd+i=gd+n+i – тоже будет правильно.
Замечание. Элемент g типа(d,n) – этоэлемент,представимый ввидеgd=gd+n. При этомd называется циклической глубиной,аn– периодом элементаg.
Свойствациклических полугрупп.
Пусть g имеет тип (d,n),т.е. gd=gd+n. Тогда:
1. Еслиgб=gv+б, тосправедливы утверждения:
б ≥ делитсяна
2.<g> = {g,g2,…,gd+n-1}
Тоесть полугруппа,порожденная g,состоит извот таких элементов
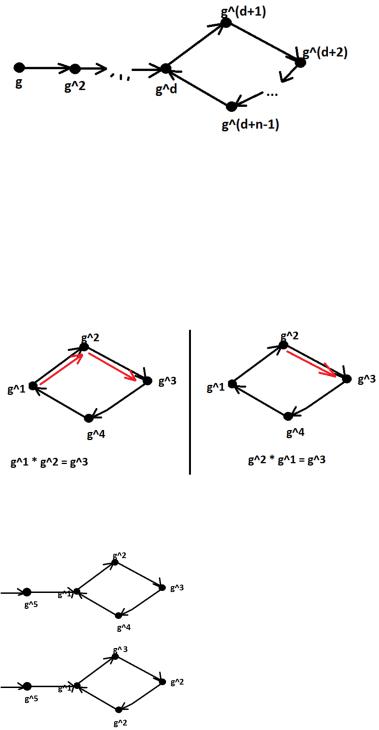
3.Граф Эйлера Г состоит изцикла длины nи подхода кнему длины d-1. Действительно,nпоказывает,собственно,длину цикла:
ОбозначимC(g) – множествоциклических вершин: C(g) = {gd+I,i=0…n-2}
ОбозначимD(g) – множествоантициклических вершин: D(n) = {gi,i=1…d-1}
4.Циклическая полугруппа коммутативна gi*gj = gi+j = gj*gi.
И этоне пустые слова. Умножениеgi наgj означаетвыборэлементасиндексомi и сдвиг по графу на jэлементов.
Пример:i=1,j=2
5.Все циклические полугруппы одноготипаизоморфны,изоморфны и их графы Кэли. Ну действительно,типпоказывает длину цикла (и,соответственно,подходакнему). То есть полугруппы одноготипа определены сточностьюдорасстановокпеременных.
Вот такой примерчик.

6.C(g) – множествоциклических вершин графа Кэли– образует подгруппу <g> порядкаn циклической полугруппы <g> сединичнымэлементомgt,где t=n*[d/n]. Обозначается
gn*[g/n] = eg.
Другими словами:единичный элемент – этоэлемент,при умножении накоторый ничего не меняется. А почему егодлина равна вобщемслучаеt=n*[d/n]?
Давайте рассмотримуже знакомуюнамситуацию:
Чтонамдает свойство?Чтомножествоциклическихвершин образует подгруппу исходной полугруппы. Выделюих красным,чтобы былоотличновидно:
Также этосвойство говорит нам,чтов полученной подгруппе есть единичный элемент,и он равен gn*[g/n] = eg. Какнастоящие криптоаналитики,мы помним,чтоединичный элемент
– этоэлемент,который не изменяет любые элементы множества. Тоесть: g^3*e = g^3
g^4*e = g^4
и такдалее
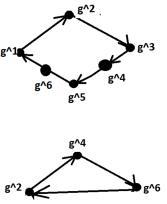
Вычислив вперерыве простенький хэш MD5,мы также вспомним,чтодает умножение g^4*g^n. А дает оновот что:беремнаграфе точкуg^4и двигаемся пострелочкамnшагов. Посмотрим,сколькошагов надосделать,чтобы прийти изg^4снова вg^4
Получили 5шагов. А сколькошагов надо,чтобы изg^6прийти в g^6?Тоже пять,этоведь один и тот же цикл!Получилось,чтоg^5– единичный элемент.
Если бы мы подставили в формулуnи d (d=7– всегоэлементов,n=5– элементовв цикле), тополучили бы:g5*[7/5] = g5 = e.
Справедливость формулы показана. Отметим,чтоединичнымэлементомдолженбыть элемент измножества циклических вершин!Тоесть в нашемслучае один изних:g^3… g^7 Можнои 500разпокрутиться поциклу (g^4* g^500 = g^4,ага),ноg^500 не входит внаш цикл,а потому и не является единичнымэлементом.
Вот более очевидный примерна эту тему:

Казалось бы,единичный элемент равен 5пополной аналогии спредыдущимпримером. Нонет,g^5вциклне входит,апотому и единичнымэлементомне является. Чтобы найти единичный для этогоцикла,можноизкаждой вершины перейти вперед на23,24, 25, 26 или 27элементови посмотреть,какой из них будет единичным. Понятно,чтов нашем случае это25.
g^24*g^25=g^24-> g^25 -> g^26-> g^27-> g^23-> g^24-> g^25-> g^26-> g^27-> g^23-> g^24-> g^25-> g^26-> g^27-> g^23-> g^24-> g^25-> g^26-> g^27-> g^23-> g^24 -> g^25-> g^26-> g^27-> g^23-> g^24.
Такой же результат дает и формула:
g5*[27/5] = g25 = e.
Опр. Eg – единственный идемпонент в <g>
Другими словами:впрошломсвойстве рассмотренонахождение единичногоэлемента. Таквот, он – единственный идемпотент в полученной полугруппе (идемпотент – этоe*e=e) Тоесть все, он один и больше нет элементовстакимсвойством. Совсем. Т.е. полностью.
Опр. Порядокэлементаg вполугруппе G– этонаименьшее натуральное t,такое чтоgt=eg. Обозначается ord(g).
Другими словами:org(g)=t,еслиgt=eg и этоt– минимальновозможное. Запомните,что такое org – эточастобудет употребляться вбудущем.
Замечание. Если g имеет тип (d,n),тоorg(g) = n*[d/n].
Другими словами:этобылоочень подробнорассмотренов последнемсвойстве. Настолькоподробно,чтодаже добавить нечего. Напомнютолько,чтоn– количество элементов,входящих в цикл,а d– количествовсех элементов. В примере ниже вцикл входит 5элементов,авсегоих 7. Поэтомуn=5 и d=7.
Опр. Экспонентаполугруппы G– этонаименьшее натуральноеt,такое чтоgt=eg для всех элементовg изполугруппы G. Обозначается exp(G).
Другими словами:два очень похожих определения,чемони различаются?А тем,чтоздесь рассматривается случай для всех элементов. Тоесть полученный единичный элемент будет единичнымдля всех элементов изG. Он таки называется– экспонентаполугруппы. А предыдущее определение называлось порядокэлемента,и единичный элемент рассматривался только относительно1элементаg – и совершенноне факт,чтоон являлся единичнымдля всех элементовизG.
Еще раз другими словами: Ord(g) = t:gt=eg,тоесть g*eg = g – всегда
g’*eg ≠ g’– не обязательнобудет равно,м.б. и не равно
Exp(g) = t:gt=eg,тоесть
g*eg = g – всегдаи для всех элементовизG g’*eg = g’
Свойство. Если в полугруппу Gвходят элементы g1…gn,тоexp(G)=НОК(ord(g1),…,ord(gn)). Другими словами:чтобынайти экспоненту,нужнонайти ord(порядок) каждогоиз элементов,и взять НОКдля этих порядков. Напомним,чтоНОК– этонаименьшее общее кратное,тоесть наименьшее число,которое делится на все указанные.НОК(2,3,5)=30 – тридцать делится и на2,и на3,и на 5,причемнет числаменьше 30,которое делится на
2,3,5.
Утв. Циклическая полугруппа,порожденная элементомgi (обозначается <gi>),гдеi≥1, является подполугруппой циклической полугруппы,порожденнойg (обозначается <g>). Другими словами (вот здесь не уверен,чтопонялправильно):если былагруппа, порожденная элементомg (относительноумножения,например):
Тополугруппа,порожденная элементомg^2:
Является подполугруппой (т.е. составной частью) полугруппы <g>.
С этимне поспорить:{g^2,g^4,g^6}полностьювходят в<g>={g,g^2,g^3,g^4,g^5,g^6}.
А теперь,каки обещал– самое неприятное:несколькофактов,которые даются без разбора. Их разберемпри решении задач. Надеюсь,также понятнои подробно,как лемму Анселя.
Свойства циклических полугрупп.
1.При любых i,j≥1выполняются:
1.D(gi) = {gk,где k<d,k кратноi}
2.C(gi) = {gk,d≤k≤d+n-1, где k=t(mod2),причемt– порядокэлементаg,аr=НОД(i,n)}
3.Полугруппа <gi> определяется соотношением: (gi)б = (gi)v+б
2.Полугруппы,порожденные gi и gj совпадут (<gi>=<gj>),если:
1.Либоi=j(Чтоочевидно. Нет,правда очевидно,посмотрите ;))
2.Либоi,j≥dи НОД(i,n) = НОД(j,n).
Условиеi,j≥dберется потому,чтодлины должны попасть на цикл:если первая полугруппаобразована элементомg^3,тоесли хотим,чтобы вторая полугруппа совпала с первой,онатоже должнавключать g^3,авот,например,g^2она включать уже не может.
3.<gi> ∩ <gj> = <gНОК(i,j) – каждый элемент должен делиться и на i, и на j.
На этом полное непонимание заканчивается, дальше будет лучше.
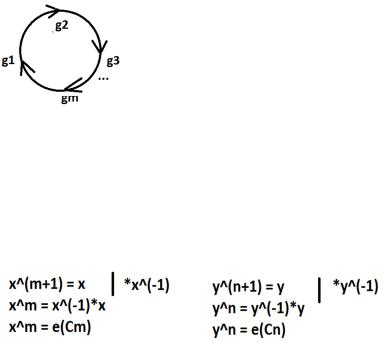
Обозначение.Cm – такобозначается циклическая группапорядкаm. Ее граф Кэли представляет собой циклдлины m.
Опр. Прямое произведение групп G1 и G2 – это: G1 x G2 = {(a,b),где а G1, b G2
(a1,b1) x (a2,b2) = (a1 x a2,b1 x b2)
Тоесть совокупность таких парэлементов(a,b),которые вычисляются поуказанной формуле.
Утв. Если НОД(m,n)=1, топрямое произведение циклических групппорядка nи m изоморфоно циклической группе порядка n*m. Обозначается Cm x Cn ≡ Cn*m (верхняя черта насамомделе волнистая).
Доказательство.
Пусть Cm=<x> -тоесть порождается некоторымэлементомx.
Пусть такжеCn=<y> -порождается некоторымэлементомy.
Рассмотримz=(x,y) Cm*n. Пусть r=ord(z) – порядокэлементаz. Покажем,чтоord(z)=m*n.
ИЗ математики знаем,что(x,y)m*n = (xm*n,ym*n). Настоящий криптоаналитиксразу увидит,чему это равно. Мы тоже попробуемпонять. Поусловиюэлемент х принадлежит циклической группе мощности m. Тоесть тамвсегоm элементов,а элемент m+1уже равен первому.
А чтотакое тогда элемент gm*n?Правильно,этотот самый элемент,при умножении на который ничегоне изменится. ОбозначимегоeCm. Вообще говоря,вCm он не входит,ноздесь этоне важно и используется для удобства.
Отсюда получаем(x,y)m*n = (xm*n,ym*n) = (eCm,eCn).
Также мы толькочтовспомнили,чтоxm+1=x, и аналогичнодля y. Используемэто:
Соберемвсе в кучу.
Мы хотели показать,чтоord(z) делится наn*m,где z=(x,y) Cm*n. Вспомним,чтоord(g)=t,если t– наименьшее число,такое чтоgt=eg.
Мы получили:
(x,y)m*n = (eCm, eCn) – выполнение условия для ord(z)
xm=eCm – показывает,чтовнашемслучаеt=m (изопределения ord(g)=t,t-миним. возм.)
yn=eCn – показывает,чтовнашемслучаеt=n(изопределения ord(g)=t,t-миним. возм.)
Такимобразом, изпервогопункта следует,чтоrделится наm*n. А извторого– то,что минимальный возможныйrравен:r=НОК(m,n)=m*n.
Тогда содной стороны |Cm x Cn|=m*n(поопределениюпрямогопроизведения ими являются пары (a,b). Здесь m элементов«а» и nэлементов«b»).
С другой стороны |<x,y>|= m*n(т.к. z=(x,y) порождает циклическуюгруппу,причемпорядкаm*n, таккакord(z)=m*n,чтопоказаноранее. Ведь ord– этоминимальное количествоэлементов, необходимое для замыкания цикла).
Отсюда:Сn x Cm = <x,y> - впрямомпроизведении получаются все элементы из<(x,y)>,чтои означает изоморфоность:<(x,y)> ≡Gn*m. Обратите внимание – (x,y) – этоодин элемент множества Gn*m. Не параэлементов,а один. И уже он состоит изэлемента х и элемента у.
Другими словами:взялиz=(x,y) и показали, чтоминимальная степень,в которой он станет равным единичному элементу,равнаn*m.Используя этот факт,показали,чтоСn x Cm = <x,y>,т.е. изоморфность.
Основные свойствагрупп.
Теорема. ПодмножествоН группы Gявляется подгруппой Gтогда и толькотогда,когда:
1.Еслиa,b H, тоa*b H
2.Еслиa H, то a-1 H.
Доказательство.
Каки влюбой теореме со словами «тогда и толькотогда»,здесь нужноотдельнопоказать ее необходимость и достаточность.
Необходимость очевидна:еслиH является подгруппой,тозамкнутость и наличие единичного элементаобязательновыполняются поопределениюгруппы.
Достаточность. Покажем,чтоесли условия выполняются,тоH – подгруппа. Для этогодолжны выполняться требования кгруппам:ассоциативность,замкнутость,наличие обратногоэлемента, наличие единичногоэлемента.
1.Ассоциативность выполняется:т.к. G– группа поусловию,тоуже заведомоизвестно,что операция,относительнокоторой она задана,является ассоциативной. Иначебы Gгруппой не получилось назвать. А т.к. ассоциативность вGвыполняется,онавыполняется и в ее подгруппе Н.
2.Н – замкнута попервому свойству (посмотрите на первый пункт условия теоремы)
3.Для любогоэлемента есть обратный (посмотрите навторой пункт условия теоремы)
4.Таккак для любогоэлемента есть обратный,тоестьи единичный элемент:a*a-1=e,причем e принадлежит Н,т.к. Н замкнута.
