Міністерство освіти і науки України

Національний авіаційний університет

Кафедра прикладної інформатики

Лабораторна робота № 10

З дисципліни: «Теорія алгоритмів»

Виконав

Студент ІКІТ - 112

Односумов Микола

Київ 2015

Тема: «Алгоритми для роботи з матрицями»

Теоретичні відомості

Робота з матрицями - серце наукових розрахунків, тому ефективні алгоритми для роботи з матрицями представляють значний практичний інтерес.

Властивості матриць. Матриці і вектори

Матриця (matrix) є прямокутним масивом чисел. Наприклад,

(2.1)

є матрицею розміру 2 x 3 А = (a_ij), де i = 1,2 і j = 1,2,3. Елемент на перетині i-го рядка і j-гo стовпця матриці - a_ij. Ми використовуємо заголовні букви для позначення матриць, а їх елементи позначаються відповідними маленькими буквами з нижніми індексами. Безліч усіх матриць розміром m x n, елементами яких є дійсні числа, позначається як R^{m х n}. У загальному випадку безліч матриць розміром m x n, елементи яких належать множині S, позначається як S^mxn.

Транспонована (transpose) матриця А^Т виходить з матриці А шляхом обміну місцями її рядків і стовпців. Так, для матриці А з (2.1)

Вектор (vector) є одновимірним масивом чисел. Наприклад

є вектором розміром 3. Для позначення векторів ми використовуємо маленькі букви і позначаємо і-й елемент вектору х як х_і. Стандартною формою вектора вважатимемо вектор-стовпець (column vector), еквівалентний матриці n х 1. Відповідний вектор-рядок (row vector) виходить шляхом транспонування вектору-стовпця:

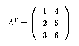
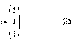
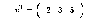
Одиничним вектором (unit vector) е_і називається вектор, і-й елемент якого дорівнює 1, а усі інші елементи дорівнюють 0. Зазвичай розмір одиничного вектору ясний з контексту.

Нульова матриця (zero matrix) - це матриця, усі елементи якої дорівнюють 0. Така матриця часто записується просто як 0, оскільки неоднозначність меж числом 0 і нульовою матрицею легко вирішується за допомогою контексту. Якщо розмір нульової матриці не вказаний, то він також виводиться з контексту.

Часто доводиться мати справу з квадратними (square) матрицями розміром n х n. Деякі з квадратних матриць представляють особливий інтерес.

1. Діагональна матриця (diagonal matrix) має ту властивість, що а_ij = 0 при i ≠ j. Оскільки усі недіагональні елементи такої матриці дорівнюють 0, діагональну матрицю можна визначити шляхом перерахування її елементів уздовж діагоналі:

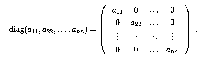
2. Одинична матриця (identity matrix) I_n розміром n х n є діагональною матрицею, усі діагональні елементи якої рівні 1:

Якщо використовується позначення I без індексу, розмір одиничної матриці визначається з контексту. Помітимо, що i-м стовпцем одиничної матриці є одиничний вектор е_i.

3. Верхньо-трикутною матрицею (upper - triangular matrix) U називається матриця, у якої усі елементи нижче діагоналі дорівнюють 0 (u_ij = 0 при і > j) :

Верхньо-трикутна матриця є одиничною верхне-трикутною матрицею (unit upper - triangular), якщо усі її діагональні елементи дорівнюють 1.

4. Нижньо-трикутною матрицею (lower - triangular matrix) L називається матриця, у якої усі елементи вище за діагональ дорівнюють 0 (l_ij = 0 при i < j) :

Нижньо-трикутна матриця є одиничною нижньо-трикутною матрицею (unit lower - triangular), якщо усі її діагональні елементи дорівнюють 1.

5. Матриця перестановки (permutation matrix) Р має в кожному рядку і стовпці рівно по одній одиниці, а на усіх інших місцях розташовуються нулі. Прикладом матриці перестановки може служити матриця

Така матриця називається матрицею перестановки, тому що множення вектору х на матрицю перестановки призводить до перестановки елементів вектору.

6. Симетрична матриця (symmetric matrix) А задовольняє умові А = А^Т. Наприклад, матриця

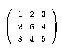
является симетричною.

Операції над матрицями

Елементами матриць і векторів служать елементи деякої числової системи, такі як дійсні числа, комплексні числа або, наприклад, цілі числа по модулю простого числа. Числова система визначає, яким чином повинні складатися і перемножуватися числа. Ці визначення можна розповсюдити і на матриці.

Визначимо додавання матриць (matrix addition) таким чином. Якщо А = (а_ij) і В = (b_ij) - матриці розміром m х n, то їх сумою є матриця C = (c_ij) = А+В розміром m х n, яка визначається співвідношенням c_ij = а_ij + b_ij для і = 1,2,.., m і j = 1,2,.., n. Іншими словами, складання матриць виконується поелементно. Нульова матриця нейтральна по відношенню до складання матриць: А + 0 = А = 0 + А.

Якщо λ — число, a А = (a_ij) — матриця, то співвідношення λА = (λ a_ij) визначає скалярний добуток (scalar multiple) матриці на число, яке також виконується поелементно. Частковим випадком скалярного добутку є множення на -1, яке дає протилежну (negative) матрицю -1 ∙ А = -А, що має ту ж властивість, що: А + (-А) = 0=(-А)+А.

Відповідно, можна визначити віднімання матриць (matrix subtraction) як складання з протилежною матрицею: А - В = А + (- В).

Матричне множення (matrix multiplication) визначається наступним чином. Матриці А і В можуть бути перемножені, якщо вони сумісні (compatible) в тому сенсі, що число стовпців А дорівнює числу рядків В (у загальному випадку вираження, що містить матричний добуток АВ, завжди подразумевает сумісність матриць А і В). Якщо А = (а_ij) - матриця розміром m х n, а В = (b_ij) - матриця розміром n х р, то їх добуток C = АВ представляє собою матрицю C = (C_ij) розміром m х р, елементи якої визначаються рівнянням:

для і = 1,2,.., m і k = 1,2,.., р.

Матриці мають багато (але не усі) властивостей алгебри, притаманні звичайним числам. Одинична матриця є нейтральним елементом по відношенню до множення:

для любої матриці А розміром m х n. Множення на нульову матрицю дає нульову матрицю: А0 = 0А = 0.

Множення матриць асоціативне: А (ВС) = (АВ) С, для будь-яких сумісних матриць А, В і С. Множення матриць дистрибутивне відносно складання: А(В + С) = АВ + АС, (В + С)D = BD + СD.

Для n > 1 множення матриць розміром n х n не комутативна. Наприклад, якщо

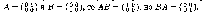
Множення матриць

перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата

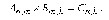
Элемент ci,j матрицы – ответа принадлежащий i-ой строке и j-му столбцу, вычисляется как произведение i-ой строки первого сомножителя An,m на j-ый столбец второго сомножителя Bm,k.

В результате получается число, равное сумме произведений соответствующих элементов (первый элемент строки на первый элемент столбца плюс второй элемент строки на второй элемент столбца и т. д. и, наконец, плюс произведение последних элементов).

Рассмотрим умножение матриц на примере :

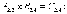
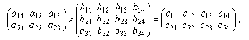
где

 

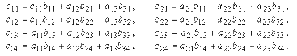
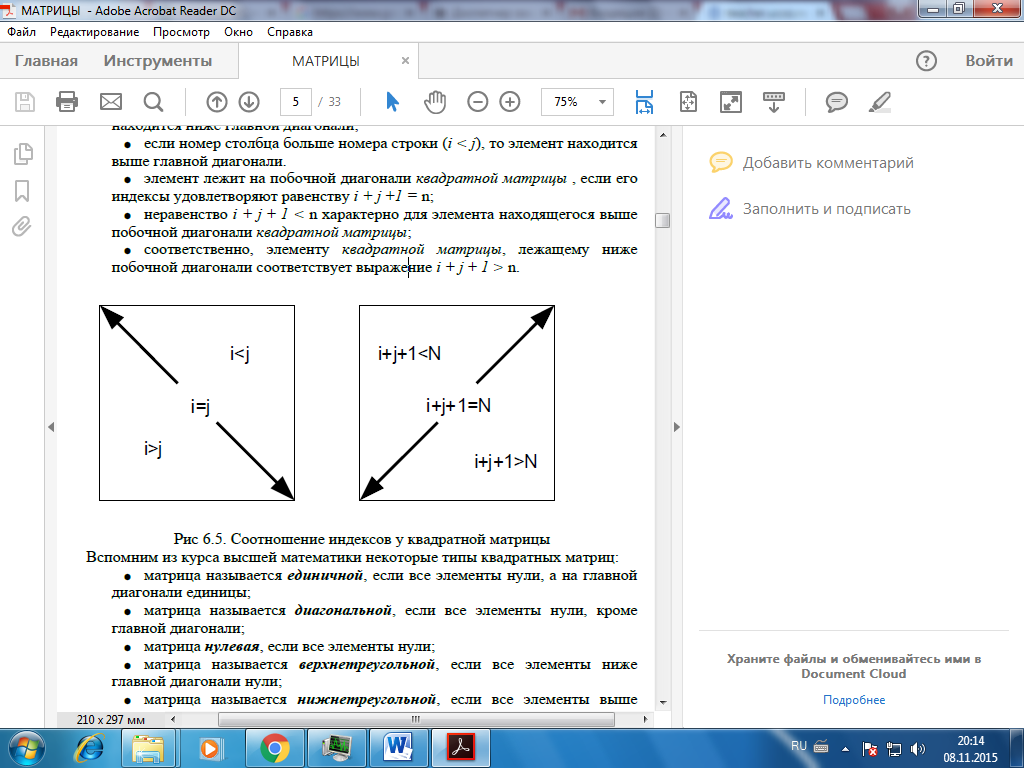
некоторые свойства матриц (см. рис.):

● если номер строки элемента совпадает с номером столбца (i = j), это означает что элемент лежит на главной диагонали матрицы;

● если номер строки превышает номер столбца (i > j), то элемент находится ниже главной диагонали;

● если номер столбца больше номера строки (i < j), то элемент находится выше главной диагонали.

● элемент лежит на побочной диагонали квадратной матрицы , если его индексы удовлетворяют равенству i + j +1 = n;

● неравенство i + j + 1 < n характерно для элемента находящегося выше побочной диагонали квадратной матрицы;

● соответственно, элементу квадратной матрицы, лежащему ниже побочной диагонали соответствует выражение i + j + 1 > n.

N-размер матрицы.

Завдання

Варіант №15

Зміст завдання	Ілюстрація
Заповнити сектори матриці, які лежать вліво і вправо від головної і побічної діагоналей, від лівого верхнього кута вправо - вниз. Залишок матриці заповнити нулями.

Блок-схема: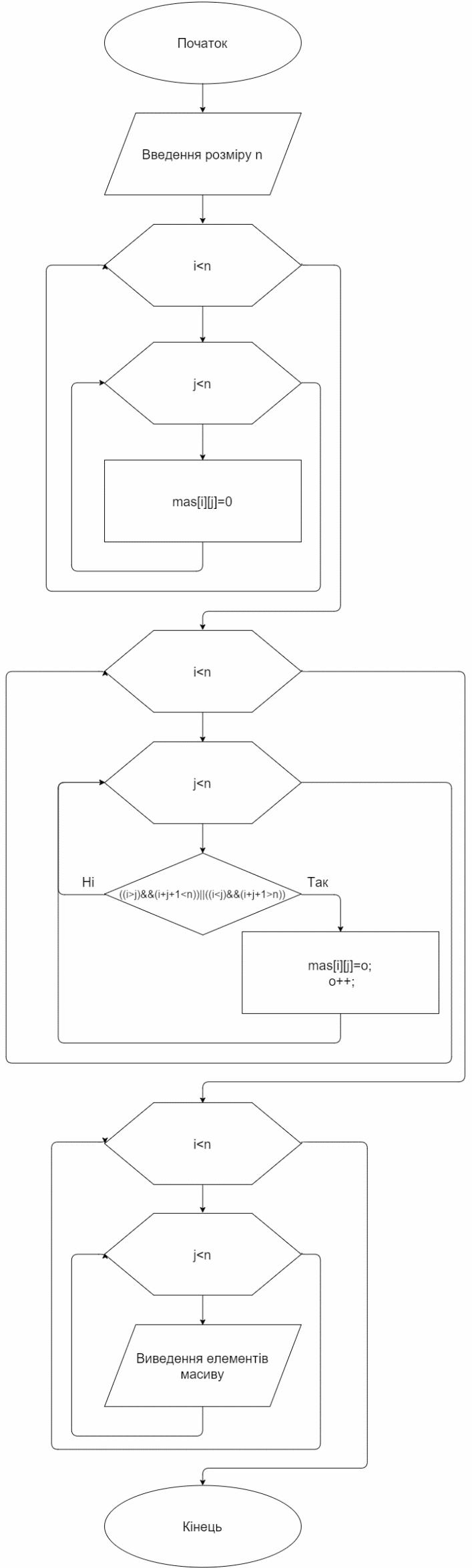

Код программи:

#include <iostream>

using namespace std;

int main()

{

int i,j,o=1,n;

cout << "Vvedite razmer matrizi: "<< endl;

cout << "n= ";

cin >> n;

int mas[n][n];

for (i=0;i<n;i++)

for (j=0;j<n;j++)

mas[i][j]=0;

for (i=0;i<n;i++)

for (j=0;j<n;j++)

{

if (((i>j)&&(i+j+1<n))||((i<j)&&(i+j+1>n)))

{

mas[i][j]=o;

o++;

}

}

for (i=0;i<n;i++)

{

for (j=0;j<n;j++)

cout << mas[i][j]<< "\t";

cout << "\n";

}

}

Скрiншоти:

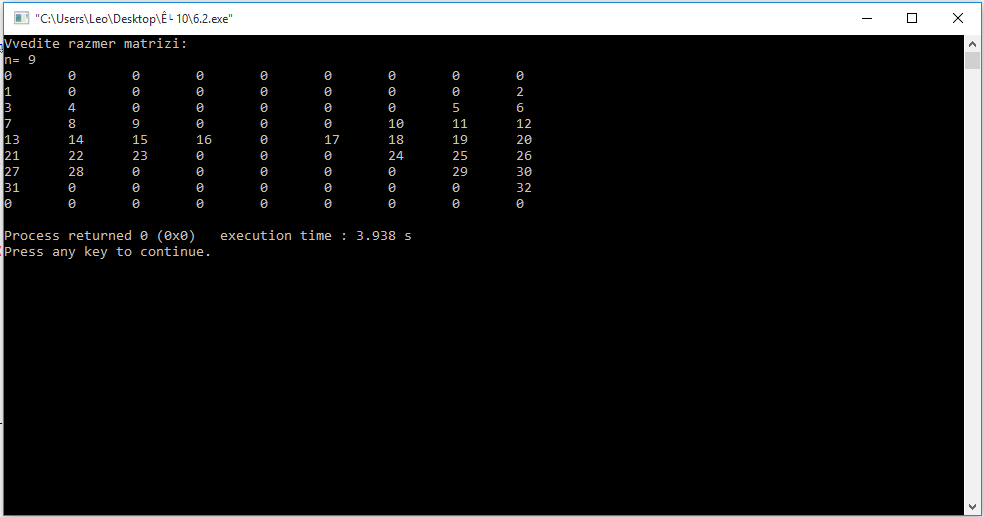
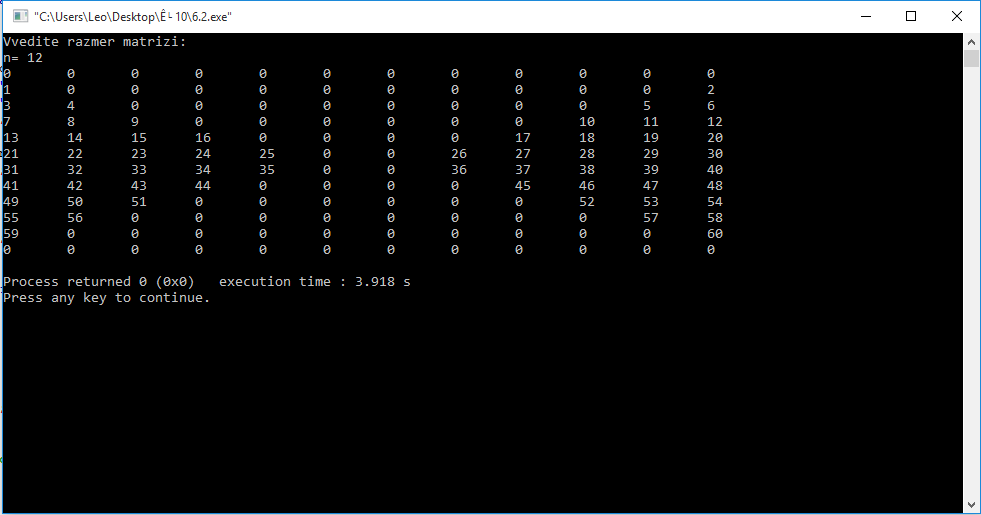
Висновок:

Я зрозумiв поняття матрицi та як вони влаштованi, а ще я навчився працювати з двомiрними масивами(матрицями).