Лекция № 1

Вектор – функция скалярного аргумента. Понятие линии. Параметризация линий с помощью вектор функций. Виды линий.

Определение 1.1 Переменным вектором называется вектор, который меняет свою длину или направление, или обе характеристики сразу.

Определение 1.2 Пусть – евклидово-трехмерные векторные пространства, - некоторый числовой промежуток. Если каждому поставить в соответствии некоторый вектор по некоторому закону, говорят, что в промежутке задана векторная функция скалярного аргумента. .

Определение 1.2’ Переменный вектор называется функцией скалярного аргумента , если всякому соответствует определенное значение вектора .

Чтобы задать вектор – функцию, её координатами вида достаточно задать эти координаты в виде скалярных функций:

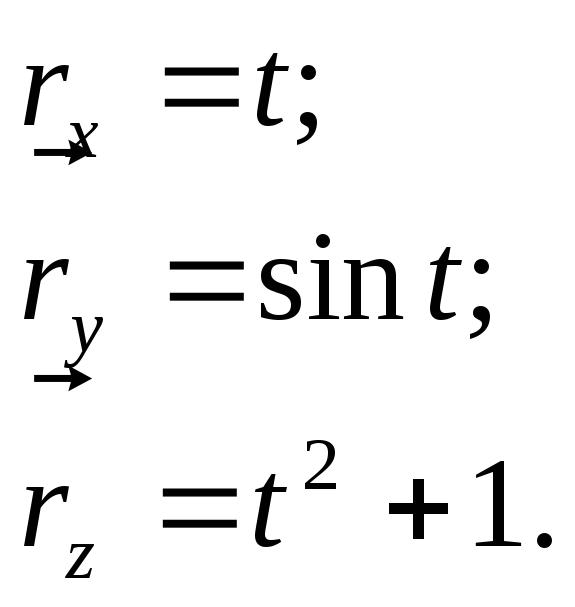
Если вектор функция задана в прямоугольной системе координат, то соответственно ей переменный вектор можно разложить по базису.

задана своими координатами

Определение 1.3 Длина вектора функции есть некоторое число, которое можно считать обыкновенной функцией от некоторого числа .

Определение 1.4 Вектор – функция называется бесконечно малой в окружности точки

, если её длина стремится к 0 при _,

Теоремы о бесконечно малых вектор функциях.

Теорема 1.5.1 Сумма (разность) бесконечно малых функций есть бесконечно малая вектор-функция.

Теорема 1.5.2 Если некоторая скалярная функция и - бесконечно малая функция, то произведение функций ,- бесконечно малая (вектор функция).

Теорема 1.5.3 Скалярное произведение бесконечно малой вектор функции есть бесконечно малая скалярная функция.

Теорема 1.5.4 Векторное произведение бесконечно малых вектор функций есть бесконечно малая вектор функция.

Теорема 1.5.5 Смешанное произведение БМВФ есть БМСФ (скалярная функция).

Определение 1.6 Пределом вектор функции при называется такой постоянный

=БМ вблизи точки

при

Из определения следует, что переменный вектор равен сумме своего предела и бесконечно малой функцией.

Теоремы о пределах.

Теорема 1.7.1 Предел суммы равен сумме пределов.

Теорема 1.7.2 При умножении вектора на скаляр и при скалярном или векторном умножении векторов.

Теорема 1.7.3 Предел постоянного вектора равен самому вектору.

Теорема 1.7.4 В условии теоремы 1.7.2. постоянный множитель выносится за знак предела.

Определение 1.8 Вектор функция называется непрерывной в точке ₀, если её предел при

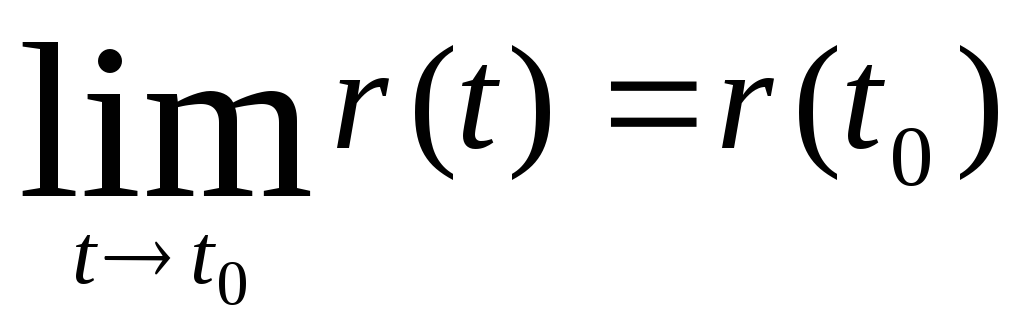
Иными словами, ВФ называется непрерывной в , если она непрерывна в каждой её точке.

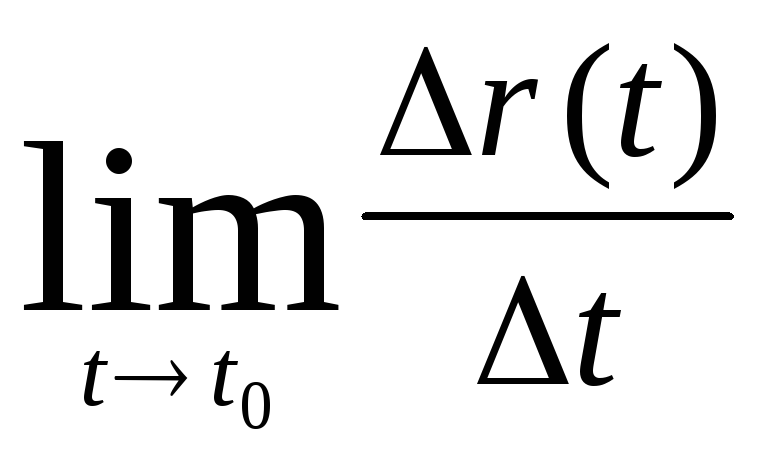
Определение 1.9 Производной ВФ называется , где

Определение 1.10 Вектор функция называется дифференцируемой на отрезке , если она дифференцируемая в каждой точке принадлежащей .

Вектор функция в ортонормированном базисе.

В ортонормированном базисе справедливо утверждение: - вектор сравнения имеет производную в , тогда и только тогда когда в этой точке некоторые производные не которых скалярных функций.

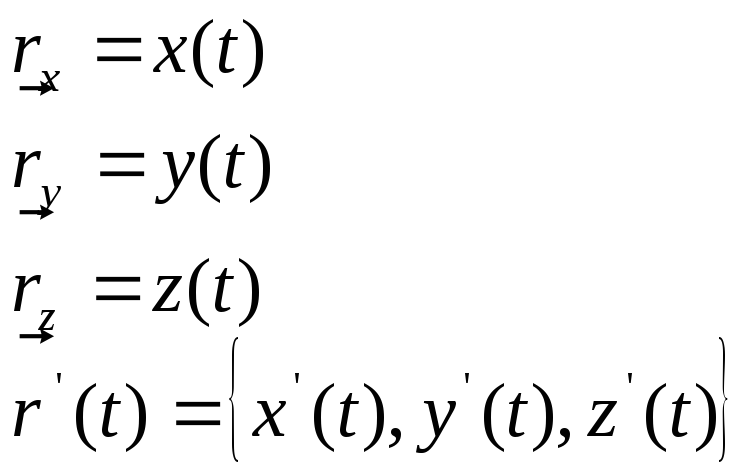
Производные от самой вектор функции и скаляров можно брать до n- порядка на

Если ﾤ - считать постоянным при t₀ то

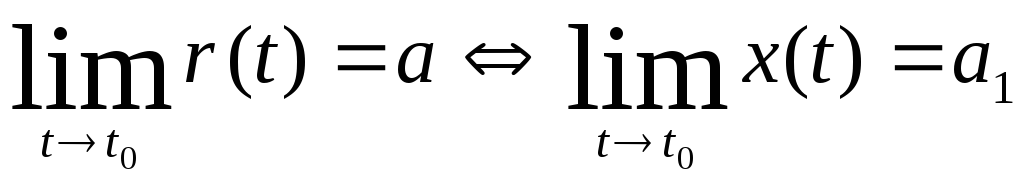
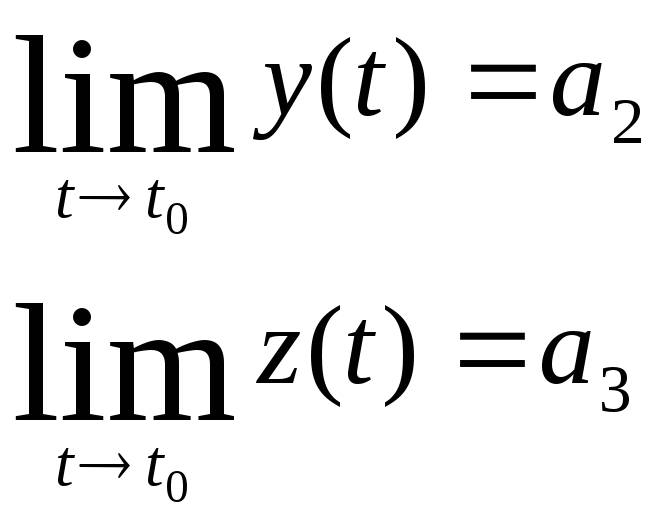
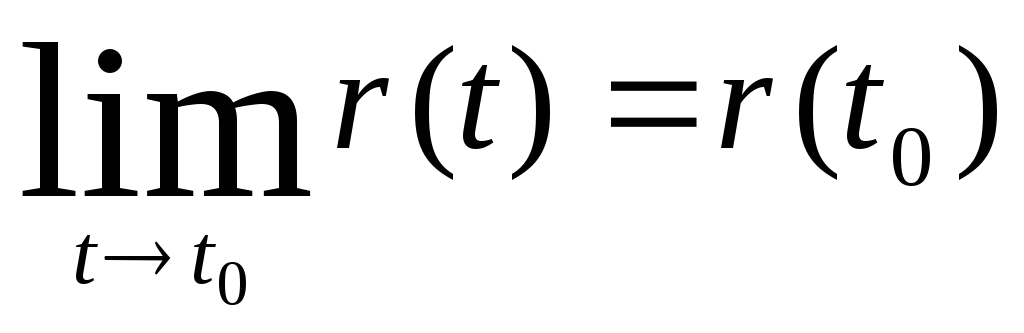Определение1.11 Если в точке имеем равенство , то векторная

функция называется непрерывной в точке .

Определение 1.12 Векторная функция называется непрерывной в промежутке , если она непрерывна в каждой точке этого промежутка.

Определение 1.13 Функция называется дифференцируемой в точке , если существует предел

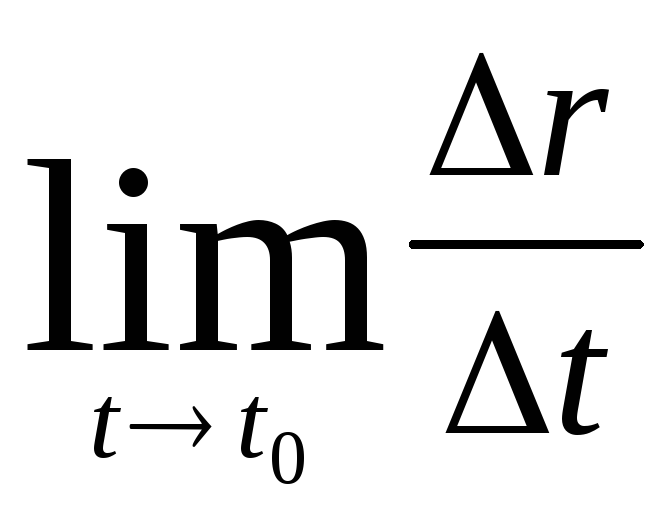. Этот предел обозначают через или через .

Теорема 1.14 Функция , заданная в промежутке своими координатами с помощью разложения , дифференцируема тогда и только тогда, когда дифференцируема каждая из функций При этом .

Пример ,

где ортонормированный базис, a,b – постоянные числа.

В данном базисе координатами являются числовые функции По теореме - дифференцируемая функция, причем

.