ГОСЫ / вопрос 14 / Лекция 3

Лекция 3

Формулы Френе. Кривизна и кручение кривой в произвольной параметризации. Винтовая линия.

Р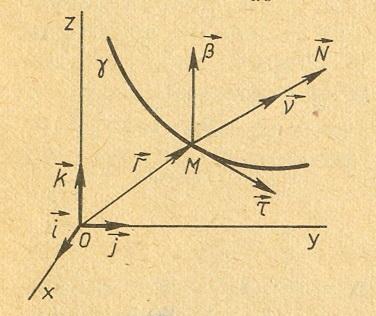ассмотрим векторы гладкой линии заданной естественной параметризацией .

1). Так как то (1)

2). Вектор – единичный вектор гладкой нормали

параллелен спрямляющей плоскости

3). . В (1) заменяем и по формулам (3) и (2). Получим

Подставим выражение в (2).

4). . Дифференцируем по s: = . Заменим и их выражениями по (3) и (4):

Формулы (3),(4),(5) называются формулами Френе, которые рассматривают связь между базисными векторами сопровождающими треугольниками, кручением и кривизной линии.

Определение 3.1. Число называется кручением линии в точке М на всей линии . Кручение есть функция параметра S.

Исходя из (5) и так как - единичный вектор, то . Кручение больше 0 тогда и только тогда, когда и противоположно направлены.

Геометрический смысл кручения.

Модуль кручения в данной точке кривой есть скорость изменения направления функции b(S) по отношению к естественному параметру S. Так как вектор b=b(S) перпендикулярен соприкасающейся плоскости, то абсолютная величина кручения характеризует скорость изменения положения соприкасающейся плоскости по отношению к параметру S.

Если линия задана в естественной параметризации, то кривизна и кручение есть функция по параметру S: .Уравнения такого вида называются натуральными уравнениями кривой и характеризуют кривую с точностью до движения, так как если у двух кривых натуральные уравнение совпадают, то кривые отличны только положением в пространстве. Если у двух кривых натуральные уравнения совпадают, то на каждой из них существует естественная параметризация, такая что в точках с одинаковыми параметрами кривизна и кручение одинаковы.

Вычислительная формула для кручения линии заданной в естественной параметризации.

- продифференцируем это равенство. Используем (5).

В

ыразим смешанное произведение векторов производных:

формула кручения (6)

Определение 3.2. Линия называется плоской, если все её точки принадлежат некоторой плоскости .

Если во всех точках гладкой плоской линии кручение равно нулю.

Произвольная параметризация.

Пусть кривая задана произвольной параметризацией своими параметрическими уравнениями:

Рассмотрим возможную замену параметра t на s, причем функция s=h(t) является допустимой заменой параметра ^-1 : ^-1

Найдем

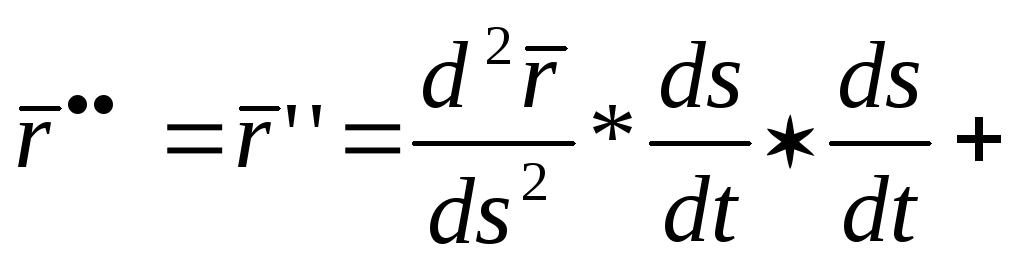
Вектор второй производной параллелен соприкасающейся плоскости, так как он выражен через вектор и .

Рассмотрим векторное произведение первой и второй производной.

Винтовая линия

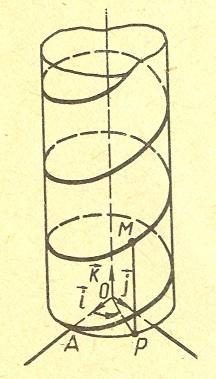Винтовая линия получена путем равномерного вращения М (х,у,z) около оси Оz и равномерного движения параллельно оси Оz. Является гладкой линией класса .

Параметрические уравнения винтовой линии: Направляющая винтовой линии совпадает с направляющей кругового цилиндра (ОХУ: , значит, винтовая линия лежит на прямом круговом цилиндре с осью Оz.

Векторное уравнение винтовой линии: .

Используя формулу , имеем: . Таким образом, .

Через М проходит прямолинейная образующая МР цилиндра, имеющая направляющий вектор Так как , то винтовая линия пересекает все образующие под постоянным углом (углом между кривой и прямой называется угол между касательной к этой кривой и данной прямой).

Длина дуги винтовой линии равна .

Вектор главной нормали: Так как (по формуле Френе), то (k – кривизна винтовой линии).

Главная нормаль винтовой линии в точке М есть перпендикуляр к оси цилиндра, проведенный через точку М, т.к. где Р – проекция М на ОХУ. Вектор главной нормали направлен противоположно вектору

Кручение винтовой линии: . Знак кручения совпадает со знаком числа b.

Винтовая линия является частным случаем достаточно широкого класса линий, называемых кривыми Бертрана. Гладкая линия называется кривой Бертрана, если для нее существует другая гладкая линия и такое отображение , что в каждой паре соответствующих точек линии и имеют общую главную нормаль.