
Лекция 12
Аксиоматический метод. Понятие об интерпретации, модели системы аксиом. Системы аксиом евклидовой геометрии. Геометрия до Евклида. «Начала Евклида».
Аксиоматический метод – способ построения научной теории, при котором в ее основу кладутся некоторые исходные положения (суждения) – аксиомы или постулаты, из которых все остальные утверждения этой теории (теоремы) должны выводиться чисто логическим путем, посредством доказательств. Назначение аксиоматического метода состоит в ограничении произвола при принятии научных суждений в качестве истин данной теории.
Построение науки на основе аксиоматического метода обычно называют дедуктивным. Все понятия дедуктивной теории (кроме фиксированного числа первоначальных) вводятся посредством определений, выражающих (или разъясняющих) их через ранее введенные понятия.
Таким образом, аксиоматическое построение некоторой теории осуществляется следующим образом:
-
Выбираются основные (первичные) понятия геометрии (чаще - точка, прямая, плоскость);
-
Между основными понятиями вводятся некоторые отношения (лежать на…, отношение порядка, конгруэнтности и т.д.);
-
Вводятся необходимые определения;
-
Вводится система аксиом, с помощью которых описываются отношения;
-
По правилам логического вывода затем доказываются следствия, леммы, теоремы, задачи.
Для осуществления аксиоматической теории в конкретном множестве объектов используется ее интерпретация (или модель), представляющая собой непустое множество, для которого указаны первичные понятия и отношения и выполнены аксиомы этой теории.
Так, например, в модели векторного пространства роль вектора может играть матрица, состоящая из вещественных чисел, или упорядоченная система вещественных чисел.
Определение 12.1. Совокупность всех следствий данной системы аксиом называется теорией той или иной математической структуры.
Так, курс элементарной геометрии – это теория евклидова трехмерного пространства. Из групповых аксиом следует теория групп и т.д.
Определение
12.2. Логическим,
или аксиоматическим, доказательством
называется конечная система высказываний
![]() ,
каждое из которых есть аксиома, или
определение, или логически ранее
доказанная теорема, задача, а последнее
есть факт, утверждаемый данной теоремой.
,
каждое из которых есть аксиома, или
определение, или логически ранее
доказанная теорема, задача, а последнее
есть факт, утверждаемый данной теоремой.
Таким образом, аксиома – тоже факт, с доказательством в один шаг (формулировка аксиомы).
Общие требования к системе аксиом: непротиворечивость, независимость (минимальность), полнота.
Определение
12.3. Система
аксиом называется логически или внутренне
непротиворечивой, если в рассуждениях
не может выполняться одновременно
![]() .
.
Иными словами,
чтобы выводы из данной системы аксиом
не приводили к возникновению двух
взаимно исключающих утверждений S
и его
отрицания
![]() (иначе теория теряет всякую ценность
для познания того или иного явления
реальной действительности, отраженного
в той или иной математической модели).
(иначе теория теряет всякую ценность
для познания того или иного явления
реальной действительности, отраженного
в той или иной математической модели).
Так, теорема Пифагора выводится из системы аксиом евклидовой геометрии и поэтому является утверждением этой геометрии. Ее отрицание, т.е. утверждение о том, что в прямоугольном треугольнике квадрат гипотенузы не равен сумме квадратов катетов, не принадлежит к числу утверждений геометрии Евклида; оно не может быть выведено из системы аксиом Евклида, т.к. эта система непротиворечива.
Определение 12.4. Система аксиом называется содержательно непротиворечивой, если существует, хотя бы одна ее модель.
Модель – эта такая конкретная реализация основных понятий и отношений между ними, в которой выполняются все аксиомы данной системы.
Критерий непротиворечивости: система аксиом непротиворечива (логически), если она содержательно непротиворечива.
Определение 12.5. Независимость системы аксиом определяется тем, что ни одна из аксиом данной системы не может быть следствием других аксиом этой системы, т.е. невыводима из других аксиом данной системы.
Чтобы доказать независимость какой-либо аксиомы от остальных аксиом системы, достаточно выбросить ее из списка аксиом, заменить отрицанием и доказать непротиворечивость полученной системы аксиом (т.е. построить модель).
В качестве примера здесь уместно привести аксиоматические исследования Н.И. Лобачевского. Он первым в своих работах четко сформулировал и обосновал, что пятый постулат Евклида не зависит от остальных аксиом геометрии Евклида (т.е. от аксиом абсолютной геометрии). Лобачевский отвергает этот постулат и заменяет его отрицанием – аксиомой Лобачевского. Используя аксиому Лобачевского и все аксиомы Евклида, кроме пятого постулата, Лобачевский развивает свою (гиперболическую) геометрию на плоскости и в пространстве.
Определение 12.6. Если в данной системе аксиом каждая аксиома независима, то и вся система аксиом называется независимой.
Критерий
независимости:
Аксиома А в системе аксиом
![]() не зависит от остальных аксиом, если
система аксиом
не зависит от остальных аксиом, если
система аксиом
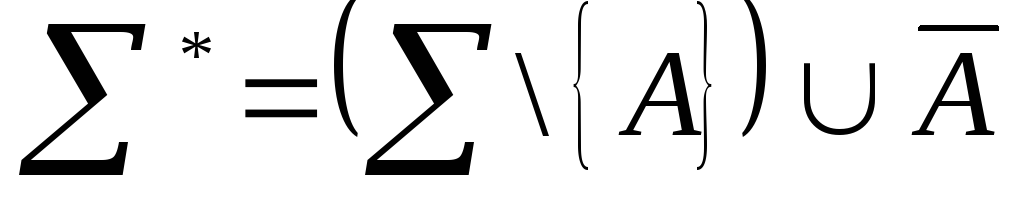 непротиворечива.
непротиворечива.
Полнота системы
аксиом:
пусть дана
система аксиом
![]() .
Аксиома D
называется расширением системы аксиом
.
Аксиома D
называется расширением системы аксиом![]() ,
если: а) она не вводит новых отношений;
б) аксиома D
не зависит от аксиом системы
,
если: а) она не вводит новых отношений;
б) аксиома D
не зависит от аксиом системы
![]() ;
в) система аксиом
;
в) система аксиом
![]() непротиворечива.
непротиворечива.
Определение 12.7. Система аксиом называется полной, если она не допускает расширения.
Определение 12.8. Две интерпретации (модели) системы аксиом называются изоморфными, если существует взаимно-однозначное соответствие между их элементами, при котором сохраняются все основные отношения.
Критерий полноты: система аксиом полна, если любые ее интерпретации изоморфны (в смысле определения).
Первые сведения о геометрии появились в Индии, далеком Египте, Вавилоне, Китае. Они умели вычислять площадь треугольника, объем усеченной четырехугольной пирамиды и площадь круга. В VII-VI в. до нашей эры геометрия появилась в Древней Греции. Основателем её был Фалес. С его именем связывают доказательство углов равнобедренного треугольника и свойство вертикальных углов. ПИФАГОР- теорема о сумме углов треугольника, теорема Пифагора, пять типов правильных многогранников и обосновал существование несоизмеримых отрезков. Демокрит – терема об объемах пирамиды и конуса. Евдокс – геометрическая теория пропорции. Архимед - правила для вычисления площади поверхности шара. Аристотель- постановка задачи о построении геометрических знаний и решение её в первом приближении. ЕВКЛИД – знаменитые «Начала», давшие систематическое изложение начал геометрии, опубликованные в 13 книгах. Первые 6- планиметрия, 7-9 – арифметика в геометрическом изложении,10- теория несоизмеримых величин, 11-13 основы стереометрии. Каждая книга начиналась с основных понятий постулатов и аксиом.
I книга основных понятий.
-
Точка есть то, что не имеет частей;
-
Линия есть длина без ширины;
-
Границы линии - суть точки;
-
Прямая есть такая линия, одинаково расположена по отношению ко всем своим точкам;
-
Поверхность есть то, что имеет длину и ширину;
-
Границы поверхности - суть линии;
-
Плоскость есть поверхность, которая одинаково расположена по отношению ко всем своим точкам;
ПОСТУЛАТЫ:
-
От всякой точки до всякой другой точки можно провести прямую;
-
Ограниченную прямую можно продлить в неограниченную;
-
Из любого центра можно провести окружность любого радиуса;
-
Все прямые углы равны;
-
(основной) Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше
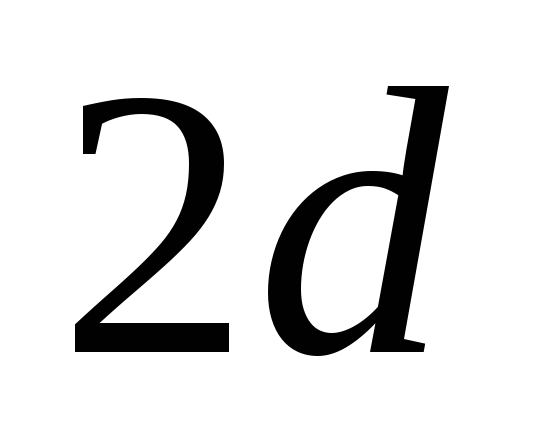 ,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(
,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(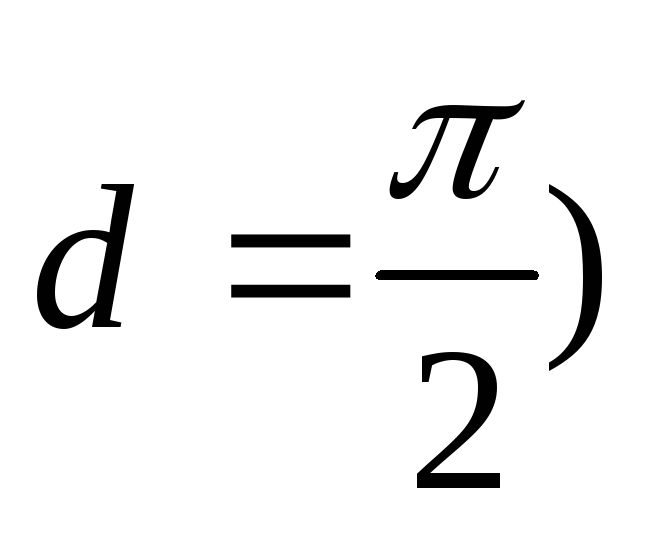
АКСИОМЫ
-
Равные одному и тому же равны между собой ;
-
Если к равным прибавить равные, то получим равные;
-
Если от равных отнимем равные, то получим равные.
-
…….
-
……
-
……
-
Совмещающиеся друг с другом равны между собой.
Затем Евклид начинает развивать свою логическую дедуктивную (от общего к частному) систему. Свою геометрию Евклид разделил на две части:
-
1 часть – без использования пятого постулата.
Определение 12.9. Геометрия, построенная на аксиомах Евклида без пятого постулата, называется абсолютной.
В этой геометрической системе содержится конечное число теорем (логических следствий из аксиом и постулатов). В трактовке Евклида их 29.
-
2 часть – добавлен пятый постулат
В этой системе (евклидовой геометрии) количество логических следствий бесконечно.
Недостатки геометрии Евклида: наиболее слабое звено – это определения.
-
Евклид пытается определить исключительно все понятия;
-
Многие определения нечетки, логически неоправданны; ряд определений даётся через неопределенные понятия;
-
Система аксиом неполная. У него нет аксиомы непрерывности (немецкий математик Дедекинд);
-
Постулаты не дают возможности объяснить такие понятии как точка, прямая лежит между двумя её другими точками; две точки плоскости лежат по разным или по одну сторону от прямой;
-
Понятия равенства у Евклида определенно с помощью движения, которые в свою очередь не получило развитие (нет аксиомы движения);
-
Убедительность логики Евклида во многих случаях подкрепляется привычками наших пространственных представлений. А это значит, что «Начала» логически безукоризненного обоснования геометрии не содержат.
На недостатки
Евклида указывал уже Архимед (жил на
100-150 лет позднее Евклида). Для того, чтобы
сравнивать отрезки, он ввел свою аксиому
Архимеда: для
любых двух отрезков
![]() и
и
![]() существует
существует
![]() ,
такое что
,
такое что
![]() .
.
Пятый постулат Евклида, попытки его доказательства. Эквиваленты пятого постулата.
В абсолютной геометрии (без использования пятого постулата) можно доказать: признаки равенства треугольника; в равнобедренном треугольнике углы при основании равны; теорему о внешнем угле треугольника: каждый из внешних углов треугольника больше любого внутреннего, с ним не смежного.
Д оказательство
(по Евклиду)
оказательство
(по Евклиду)
1.
![]() .
Тогда треугольник
.
Тогда треугольник
![]() равняется треугольнику
равняется треугольнику
![]() (по двум сторонам и углу между ними),
следовательно,
(по двум сторонам и углу между ними),
следовательно,
![]() .
Но угол
.
Но угол
![]() составляет часть внешнего угла при
вершине
составляет часть внешнего угла при
вершине
![]() .
Значит, теорема доказана.
.
Значит, теорема доказана.
Последний момент
(что угол
![]() составляет
часть внешнего угла) устанавливается
из наглядности чертежа, т.к. аксиомы
Евклида не дают возможности точно
обосновать понятия «между», «внутри»
и т.д. Кроме того, в доказательстве
использовалось понятие равенства
треугольников, которое не обосновано,
т.к. не определено движение у Евклида.
Таким образом, приведенные рассуждения
существенно подкрепляются наглядностью
чертежа.
составляет
часть внешнего угла) устанавливается
из наглядности чертежа, т.к. аксиомы
Евклида не дают возможности точно
обосновать понятия «между», «внутри»
и т.д. Кроме того, в доказательстве
использовалось понятие равенства
треугольников, которое не обосновано,
т.к. не определено движение у Евклида.
Таким образом, приведенные рассуждения
существенно подкрепляются наглядностью
чертежа.
Пользуясь теоремой о внешнем угле треугольника без помощи пятого постулата легко доказывается следующая лемма: если при пересечении двух прямых секущей накрест лежащие углы (или соответственные углы) равны, то прямые не пересекаются.
Доказательство.
П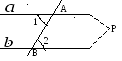 усть
при пересечении прямых
усть
при пересечении прямых
![]() и
и
![]() секущей АВ накрест лежащие углы равны
(например,
секущей АВ накрест лежащие углы равны
(например,
![]() ).
Допустим, что прямые
).
Допустим, что прямые
![]() и
и
![]() пересекаются в некоторой точке
пересекаются в некоторой точке
![]() ,
то получим треугольник
,
то получим треугольник
![]() ,
у которого один из углов при вершине
,
у которого один из углов при вершине
![]() или
или
![]() равен внешнему, что противоречит теореме
о внешнем угле. Второе утверждение
следует непосредственно из доказанного.
равен внешнему, что противоречит теореме
о внешнем угле. Второе утверждение
следует непосредственно из доказанного.
Пользуясь данной
леммой, легко доказывается (без
использования пятого постулата), что
через каждую точку М, не лежащую на
прямой
![]() ,
проходит прямая, параллельная прямой
,
проходит прямая, параллельная прямой
![]() .
.
Возникает вопрос:
сколько же прямых, параллельных прямой
![]() ,
проходит через точку М.
Ответ на этот вопрос дает следующая
теорема: если
имеет место пятый постулат, то через
каждую точку М, не лежащую на прямой
,
проходит через точку М.
Ответ на этот вопрос дает следующая
теорема: если
имеет место пятый постулат, то через
каждую точку М, не лежащую на прямой
![]() ,
проходит только одна прямая, параллельная
прямой
,
проходит только одна прямая, параллельная
прямой
![]() .
.
Доказательство:
-
П
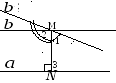 роведем
прямую
роведем
прямую
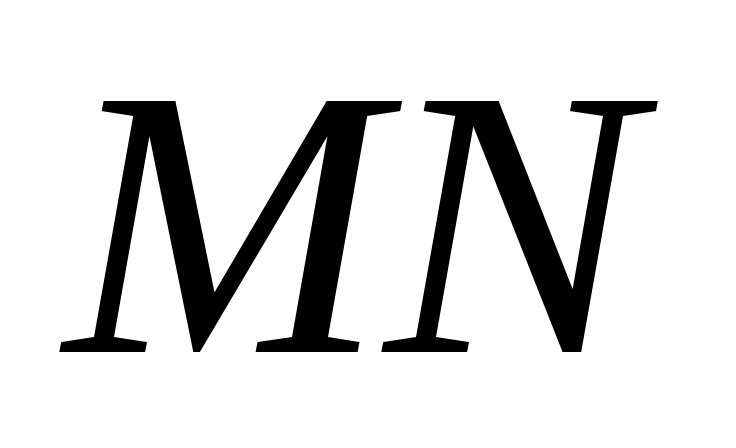 ,
перпендикулярную к прямой
,
перпендикулярную к прямой
 ,
,
 и прямую
и прямую
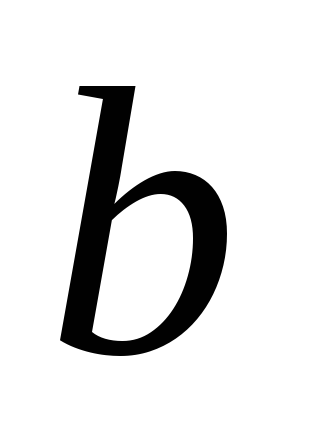 ,
проходящую через точку
,
проходящую через точку
 перпендикулярно
к прямой
перпендикулярно
к прямой
 .
Тогда прямые
.
Тогда прямые
 и
и
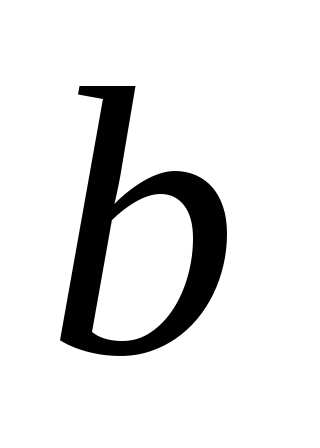 параллельны.
параллельны. -
Проведем через точку
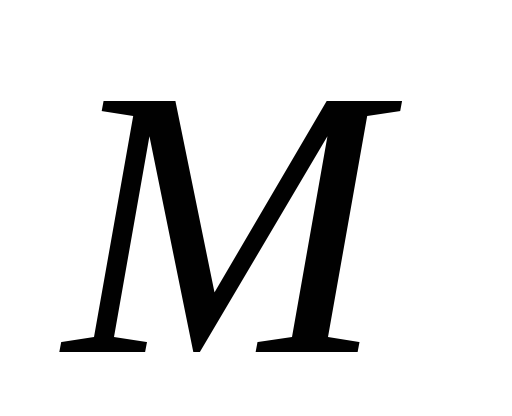 произвольную
прямую
произвольную
прямую
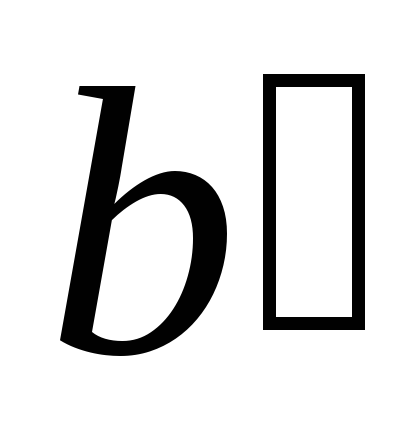 ,
отличную от прямой
,
отличную от прямой
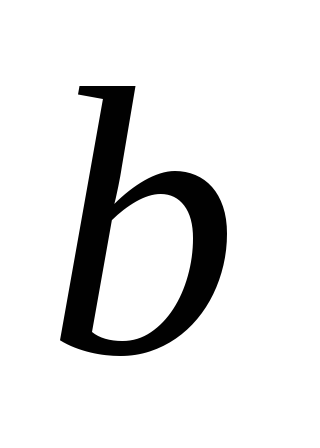 .
Один из смежных углов (1 или 2) острый
(пусть
.
Один из смежных углов (1 или 2) острый
(пусть
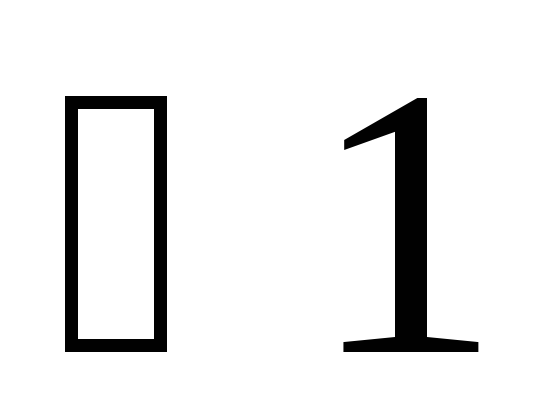 ).
При пересечении прямых
).
При пересечении прямых
 и
и
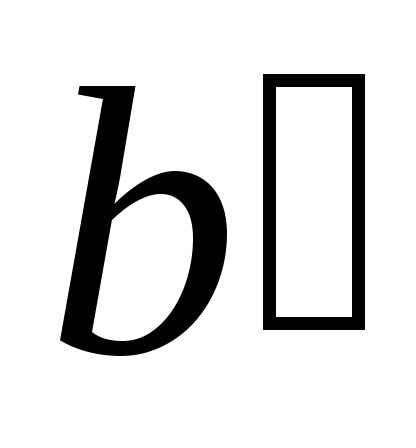 с
прямой
с
прямой
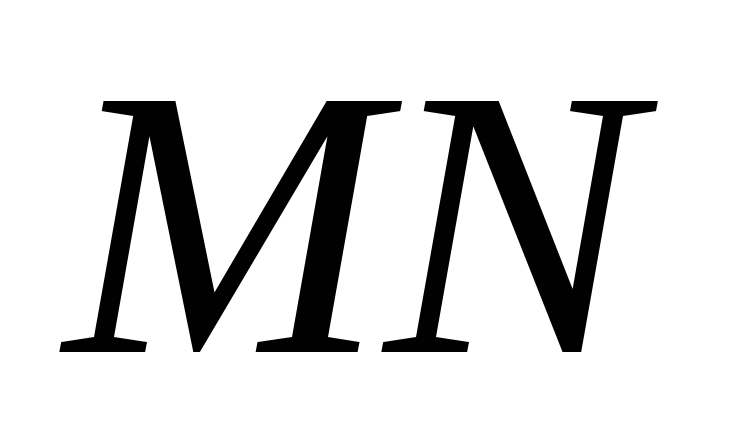 получаем
внутренние односторонние углы:
получаем
внутренние односторонние углы:
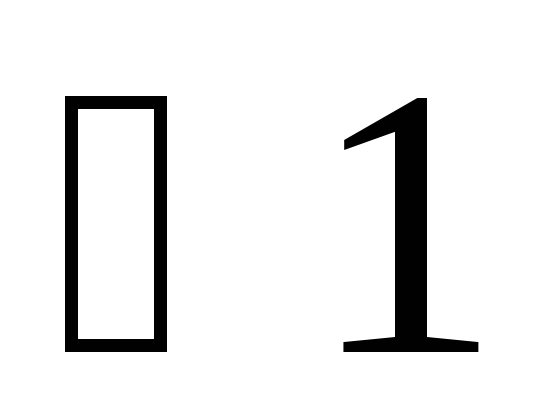 и
и
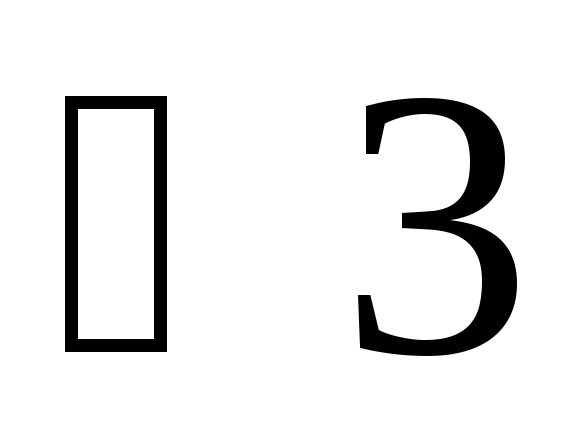 ,
сумма которых меньше двух прямых углов,
значит по пятому постулату прямые
,
сумма которых меньше двух прямых углов,
значит по пятому постулату прямые
 и
и
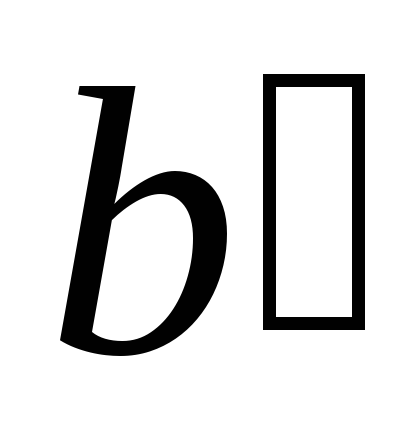 пересекаются.
пересекаются.
Д окажем
обратную теорему: если
принять, что через точку, не лежащую на
данной прямой, проходит одна прямая,
параллельная данной, то справедлив
пятый постулат.
окажем
обратную теорему: если
принять, что через точку, не лежащую на
данной прямой, проходит одна прямая,
параллельная данной, то справедлив
пятый постулат.
Доказательство.
-
Пусть при пересечении прямых
 и
и
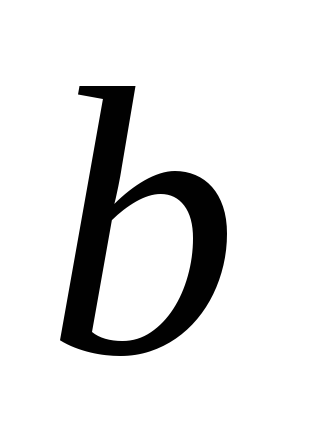 секущей
секущей
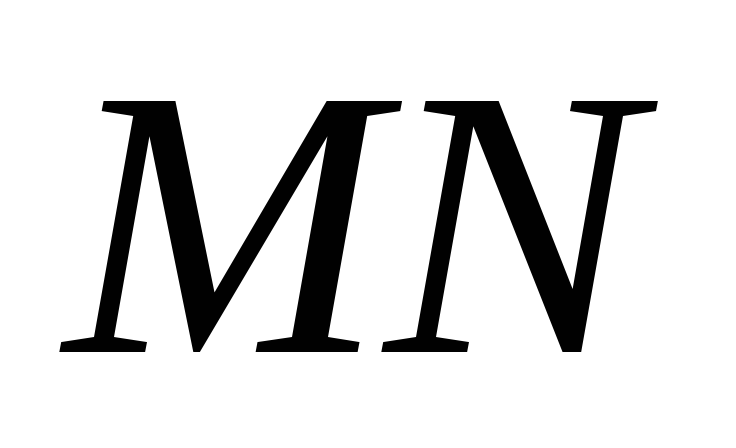 образованы
внутренние односторонние углы
образованы
внутренние односторонние углы
 и
и
 так, что
так, что
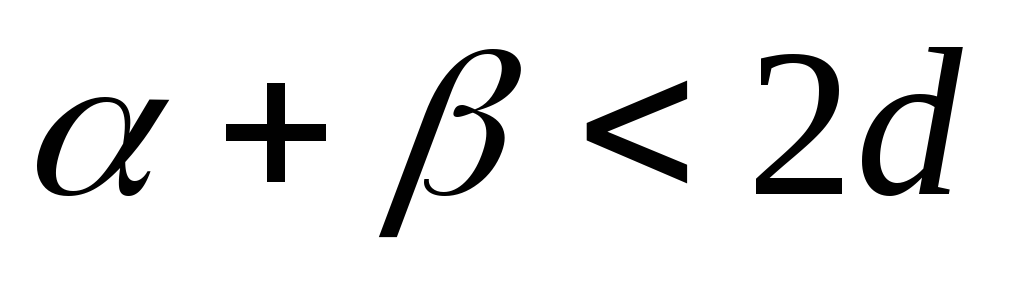 ,
где
,
где
 -
мера прямого угла. Докажем, что прямые
-
мера прямого угла. Докажем, что прямые
 и
и
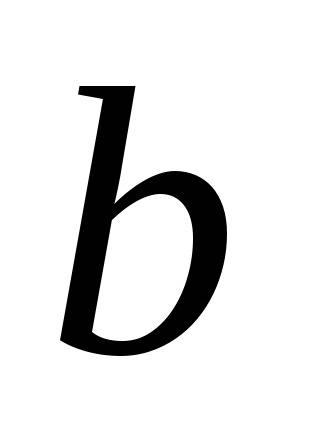 пересекаются в некоторой точке, лежащей
в полуплоскости, в которой лежат углы
пересекаются в некоторой точке, лежащей
в полуплоскости, в которой лежат углы
 и
и
 .
. -
Обозначим через
 угол смежный с углом
угол смежный с углом
 и накрест лежащий с углом
и накрест лежащий с углом
 .
Так как
.
Так как
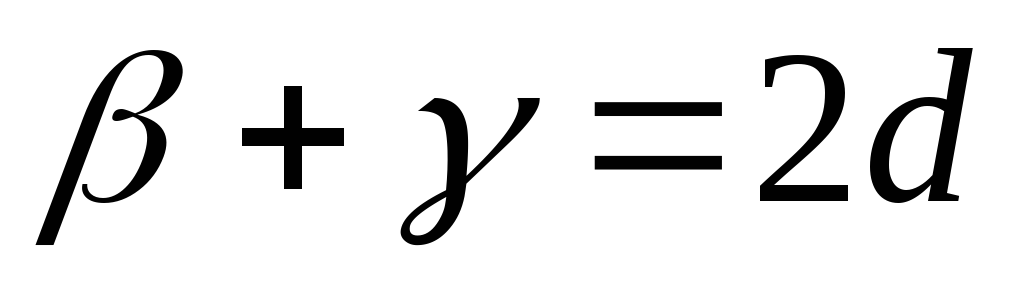 ,
то из 1) следует, что
,
то из 1) следует, что
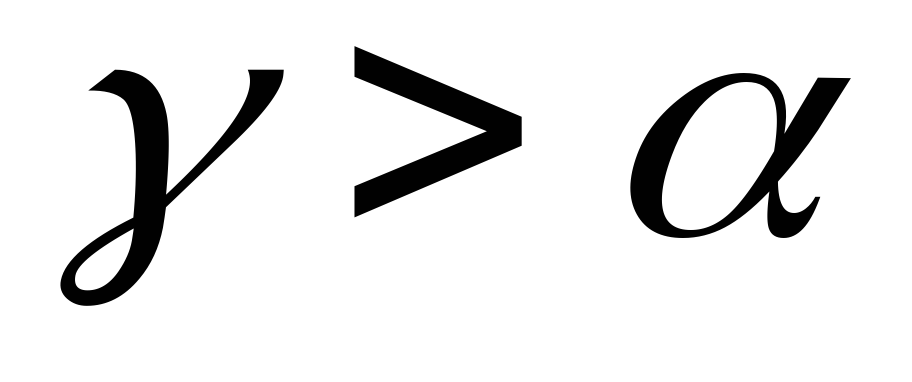 .
. -
Отложим от луча
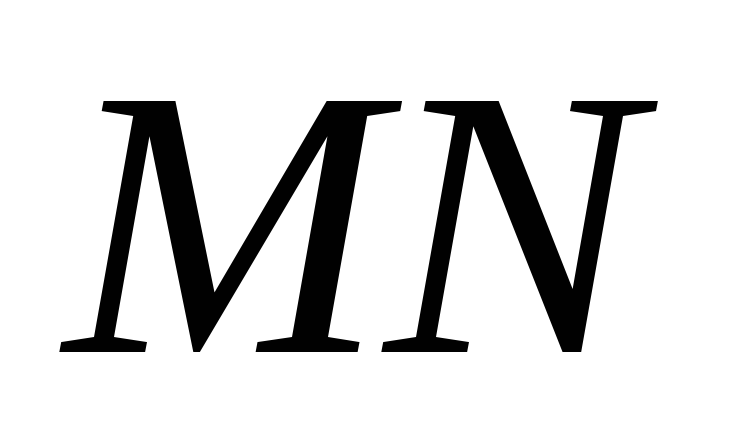 угол
угол
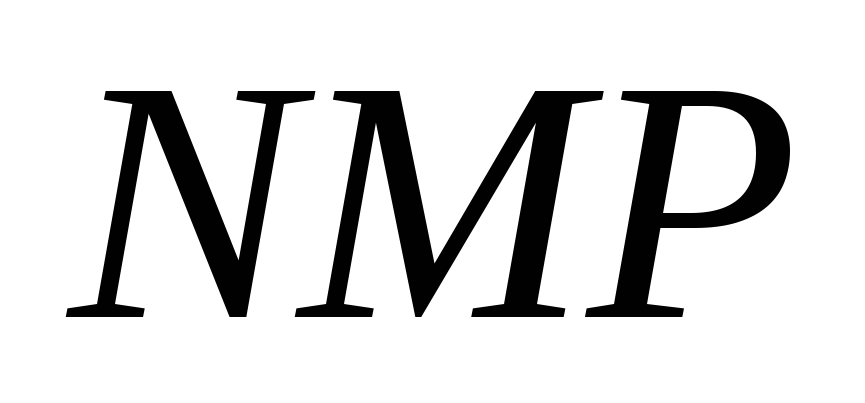 ,
равный углу
,
равный углу
 ,
так, чтобы
,
так, чтобы
 и
и
 были
накрест лежащими углами при пересечении
прямых
были
накрест лежащими углами при пересечении
прямых
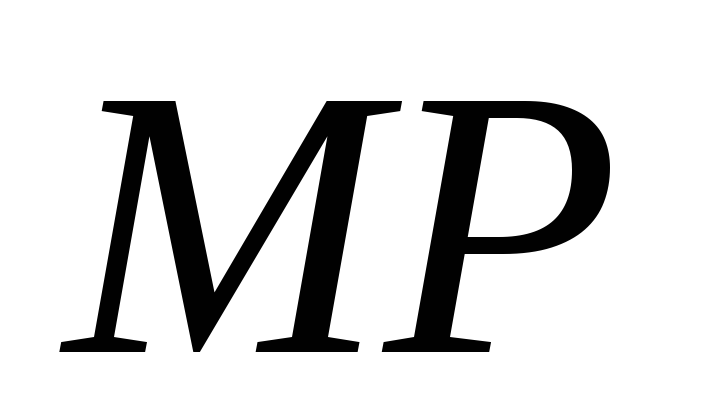 и
и
 прямой
прямой
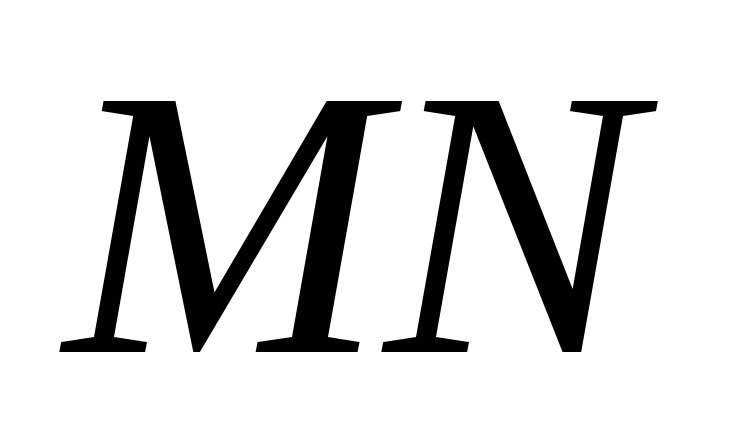 .
По лемме прямые
.
По лемме прямые
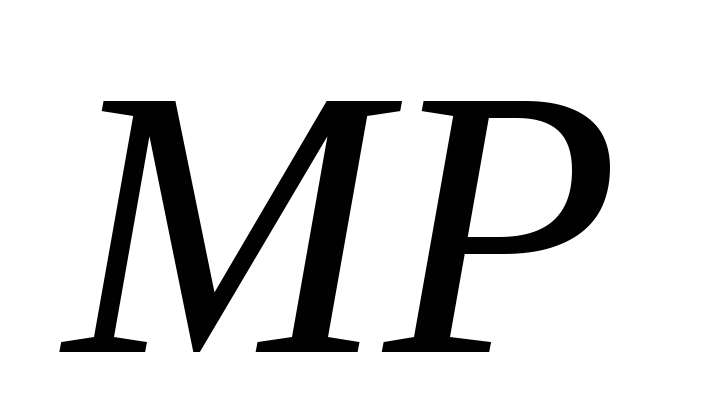 и
и
 параллельны. В силу неравенства
параллельны. В силу неравенства
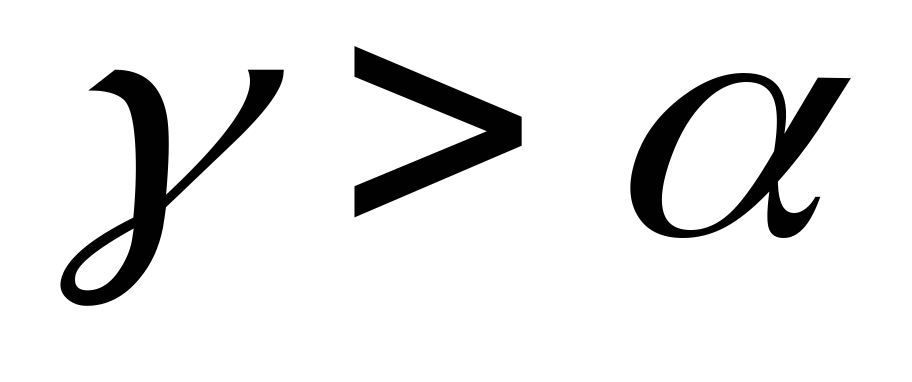 прямые
прямые
 и
и
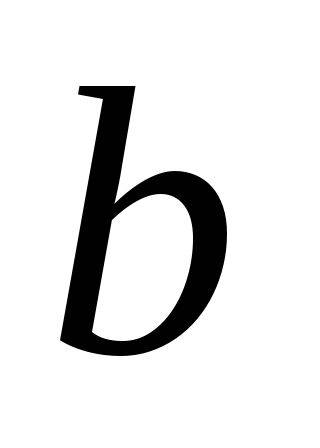 не совпадают. Так как через точку
не совпадают. Так как через точку
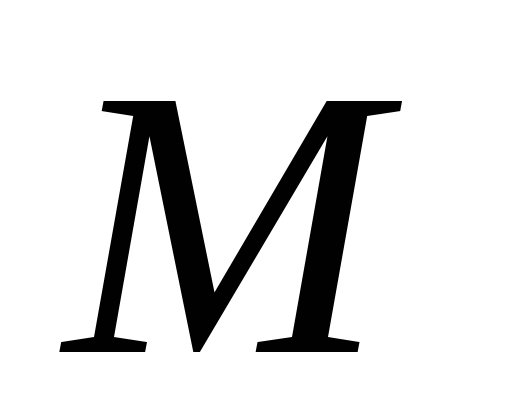 проходит
только одна прямая, параллельная прямой
проходит
только одна прямая, параллельная прямой
 ,
то прямые
,
то прямые
 и
и
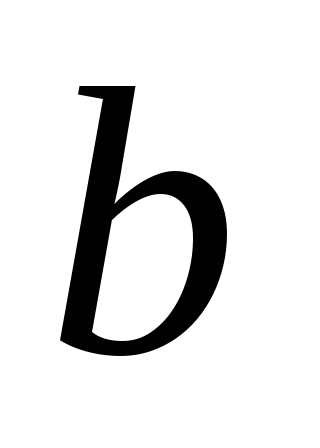 пересекаются
в некоторой точке
пересекаются
в некоторой точке
 .
. -
Если предположить, что точка
 лежит
в той полуплоскости, в которой лежит
угол
лежит
в той полуплоскости, в которой лежит
угол
 ,
то в силу неравенства
,
то в силу неравенства
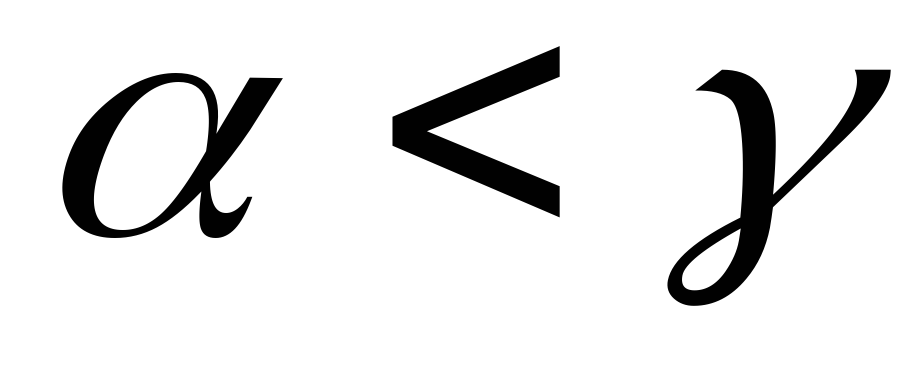 придем к противоречию с теоремой о
внешнем угле треугольника. Таким
образом,
придем к противоречию с теоремой о
внешнем угле треугольника. Таким
образом,
 -
точка той полуплоскости, в которой
лежат углы
-
точка той полуплоскости, в которой
лежат углы
 и
и
 .
.
Итак, пятый постулат эквивалентен (равносилен) так называемой аксиоме параллельности прямых: через точку, не лежащую на данной прямой, проходит не более чем одна прямая, параллельная данной.
Итак, 5 постулату
(если две
прямые при пересечении с третьей образуют
с одной стороны внутренние односторонние
углы, сумма которых меньше
![]() ,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(
,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(![]() )
в Евклидовой
геометрии отводится особое место.
)
в Евклидовой
геометрии отводится особое место.
На нем основана теория параллельных прямых, подобие фигур, теорема о сумме углов в треугольнике, теорема о сумме углов выпуклых многоугольников, тригонометрия, теория площадей и объемов. Попытки доказательства пятого постулата привели к признаку параллельности прямых, аксиом существования параллельной прямой. Пятый постулат также эквивалентен (равносилен) следующим утверждениям.
-
Сумма углов каждого треугольника равна двум прямым;
-
Существует хотя бы один треугольник, сумма углов которого равна 2d (d- прямой угол);
-
существует прямоугольник;
-
Существует пара треугольников
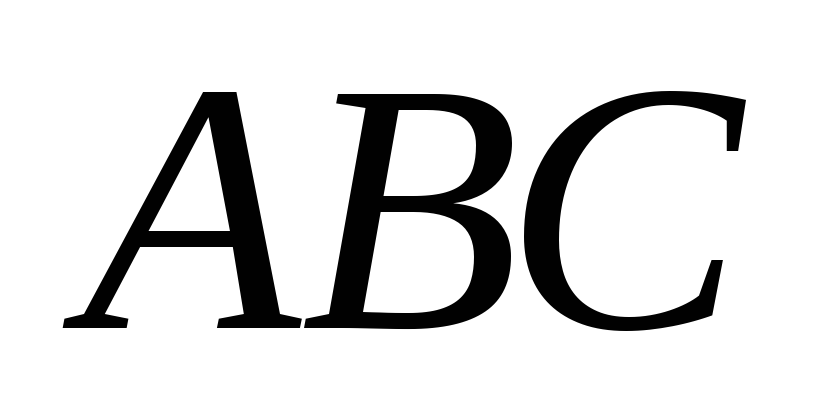 и
и
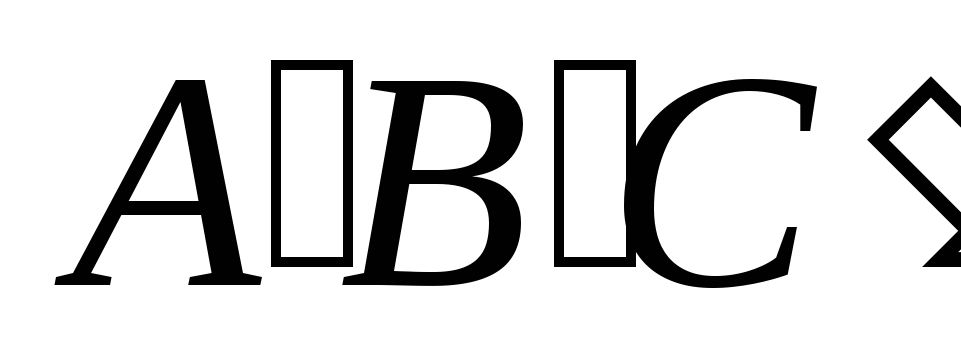 с равными углами;
с равными углами; -
Теорема Пифагора.
Со времен Евклида и до конца 19 века было множество попыток доказать 5-ый постулат (О.Хойям 1048-1023 г., Лежандр – 1750-1833 г и др.). Обычно автор доказательства незаметно для себя опирался на некоторое допущение, которое оказывалось еще одним эквивалентов 5-го постуоата. Попытки были бесплодными, но был получен ряд верных результатов, наиболее четкое доказательство которых было дано Лежандром.
