ГОСЫ / вопрос 5 / Лекция 10

Лекция №10.

Гипербола. Каноническое уравнение. Исследование формы гиперболы по ее уравнению. Характеристические элементы гиперболы. Способы построения гиперболы.

Определение 10.1. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек F₁ и F₂ той же плоскости, называемых фокусами, есть величина постоянная, меньшая чем расстояние между фокусами.

Обозначим расстояние между фокусами F₁ и F₂ через , а абсолютное значение разности любой точки гиперболы до фокусов через .

1. Введём прямоугольную систему координат таким образом, что ось Ох содержит точки F₁ и F₂, ось Oу – серединный перпендикуляр отрезка F₁F₂. Тогда фокусы F₁ и F₂ имеют координаты и

2. Пусть - любая точка гиперболы. Тогда по определению гиперболы

. (1)

3. Т.к. , то

₍₂₎

4. Преобразуем равенство (2):

Пусть , тогда .

Разделив обе части равенства на , имеем (3) , где а<с,

5. Покажем, что линия, определяемая уравнением (3), есть гипербола, то есть что всякая точка , координаты которой удовлетворяют уравнению (3) есть точка гиперболы, т.е. для нее выполняется условие :

1. Выразим в координатах ;

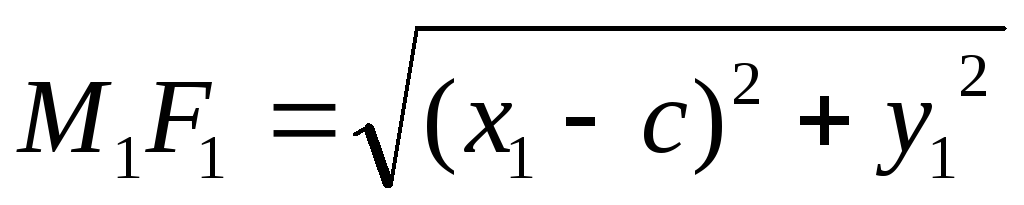2. Из уравнения (3) следует, что 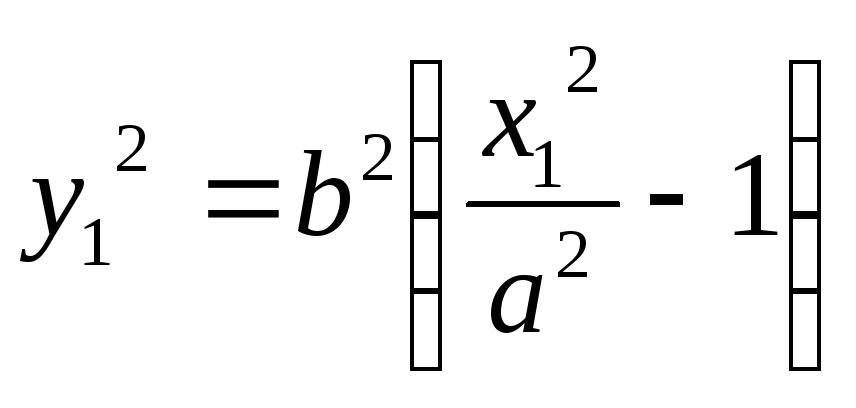. Так как 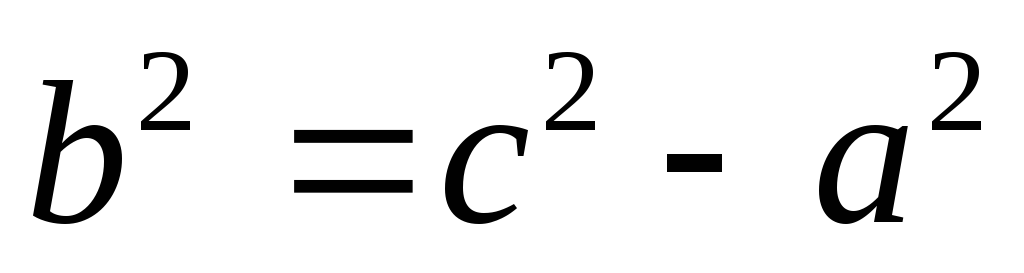, имеем ;

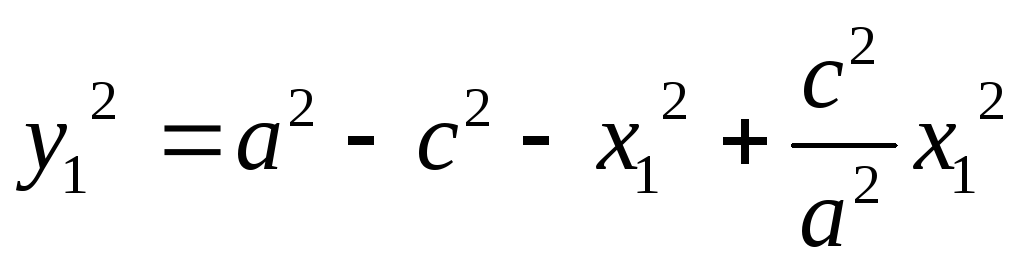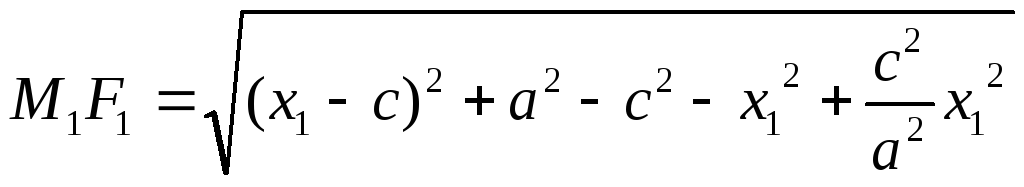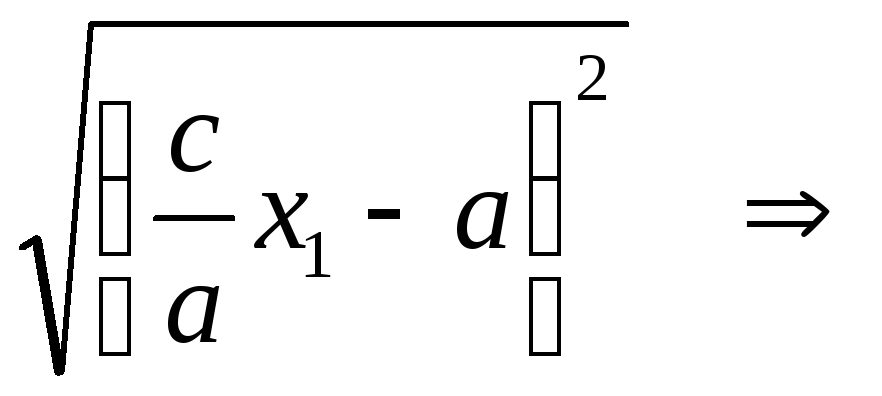
3. Из (a) и (b) следует, что = 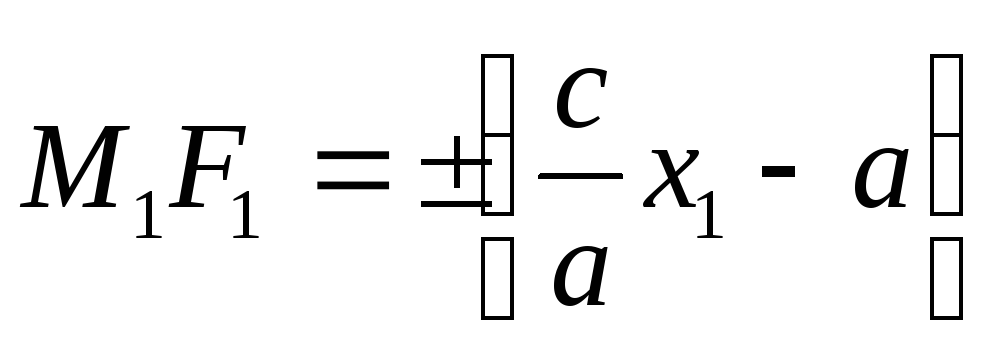, где .

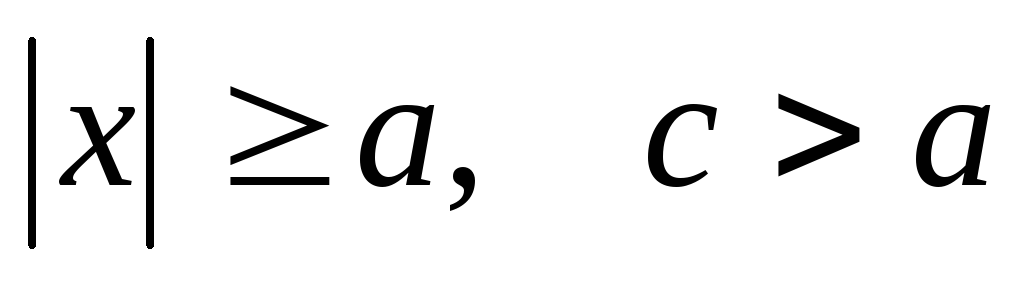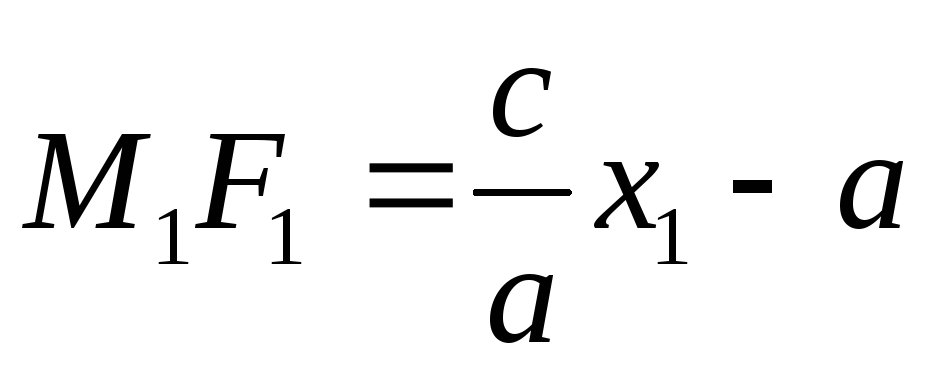4. при условии, что 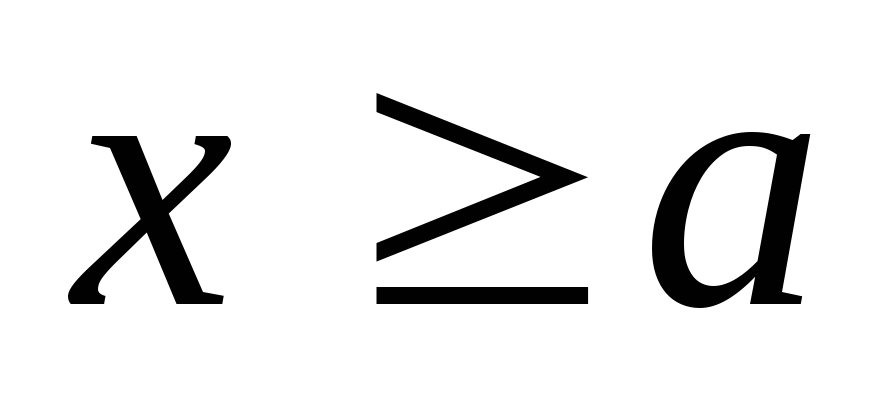и 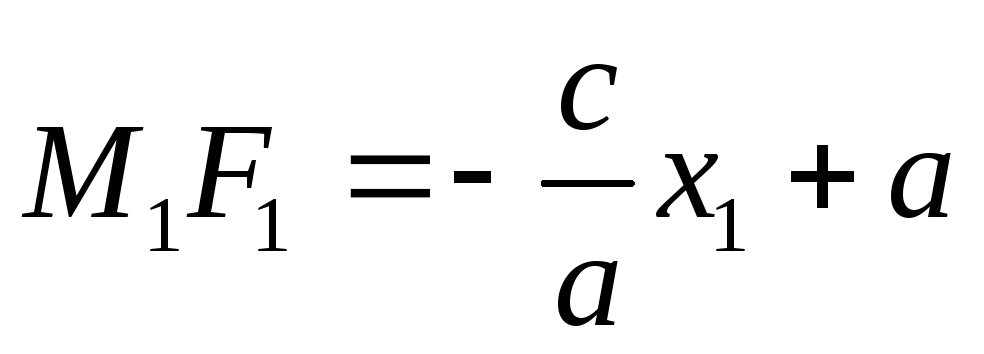, при условии, что .

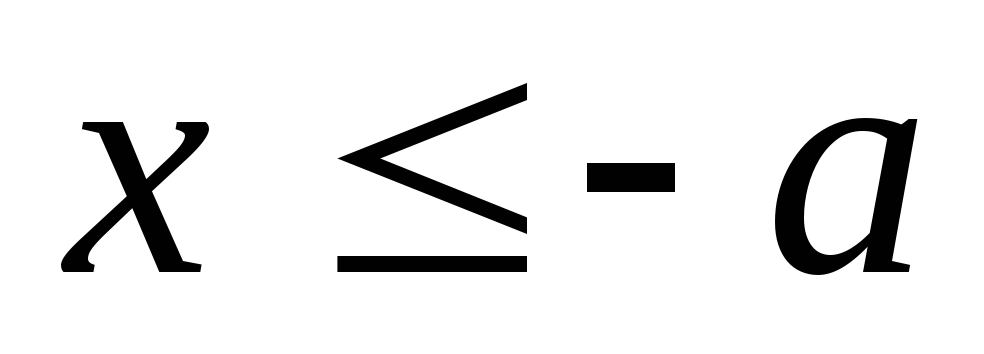5. Аналогичными рассуждениями приходим к выводу, что 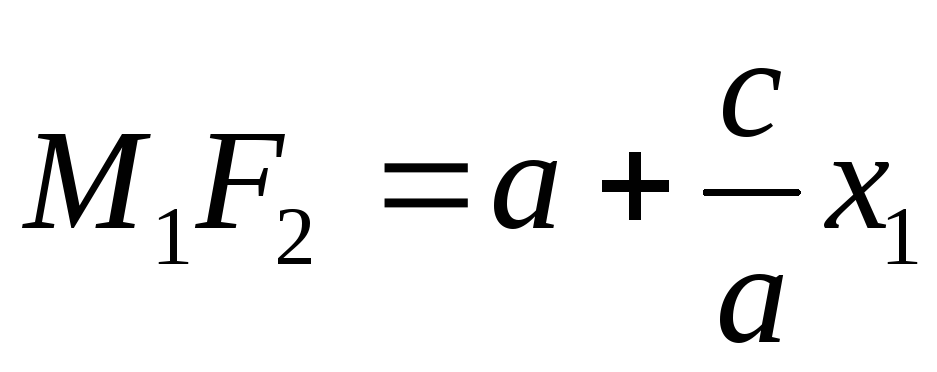при условии, что 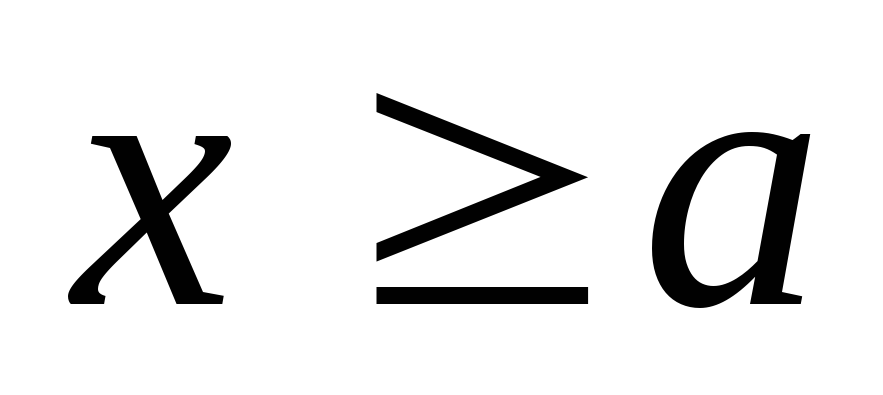; 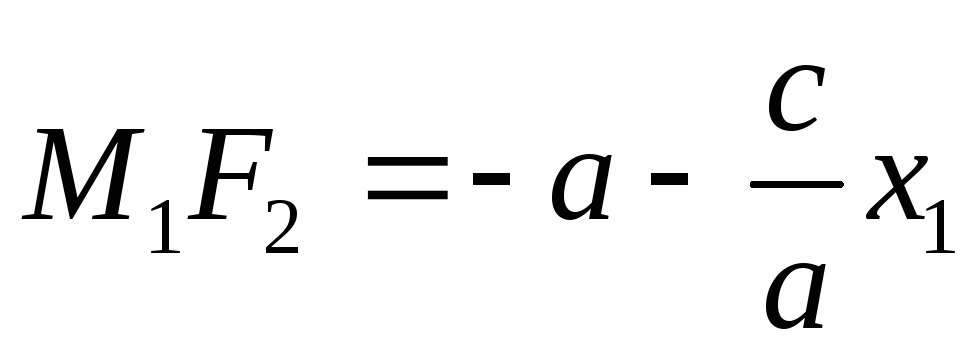при условии, что .

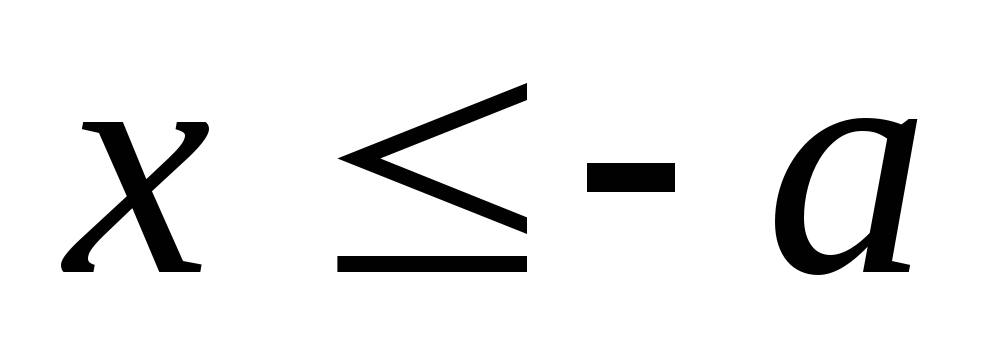6. Найдем

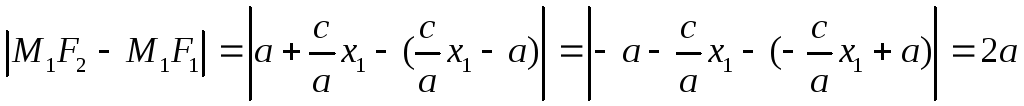
Таким образом, - каноническое уравнение гиперболы

Исследование формы гиперболы по ее каноническому уравнению

1. Из уравнения 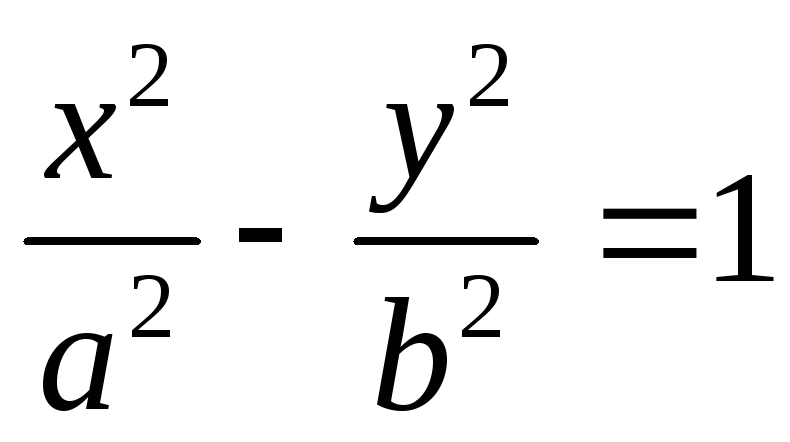следует, что 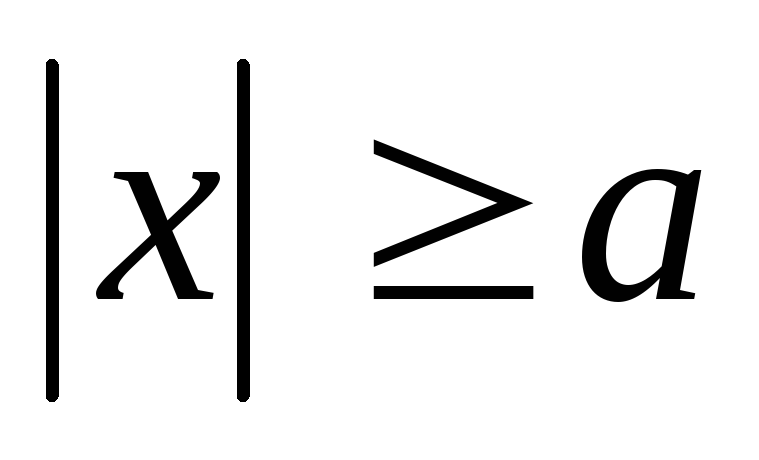. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми 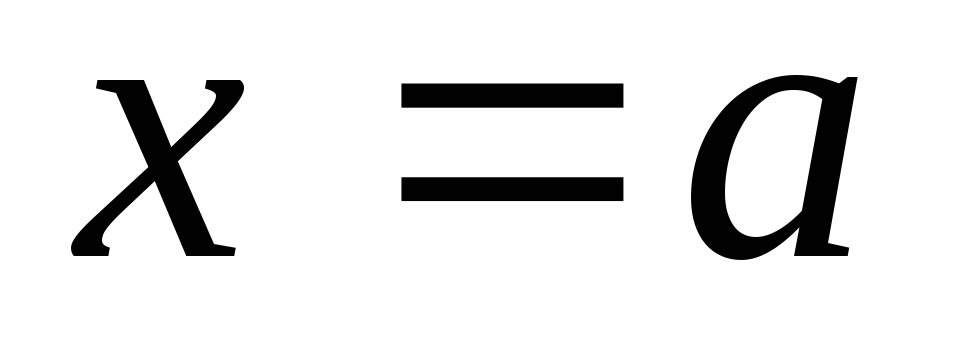и .

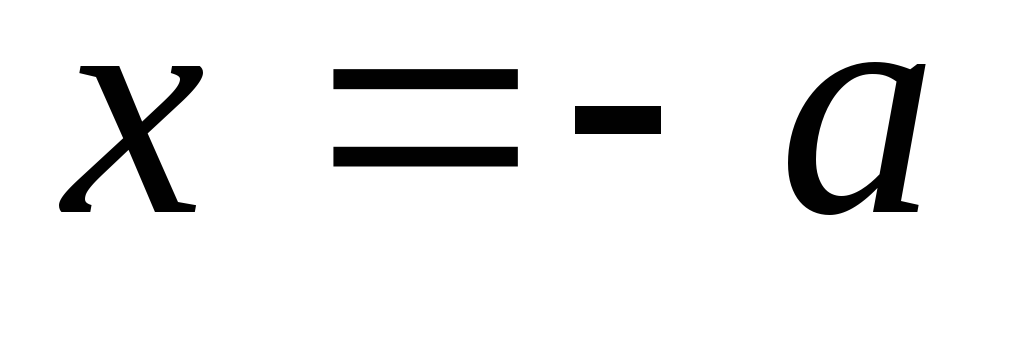2. В уравнение входят только чётные степени. Значит, гипербола симметрична относительно каждой из осей координат и начала координат. Поэтому достаточно исследовать гиперболу только в I четверти. Для первой четверти имеем:

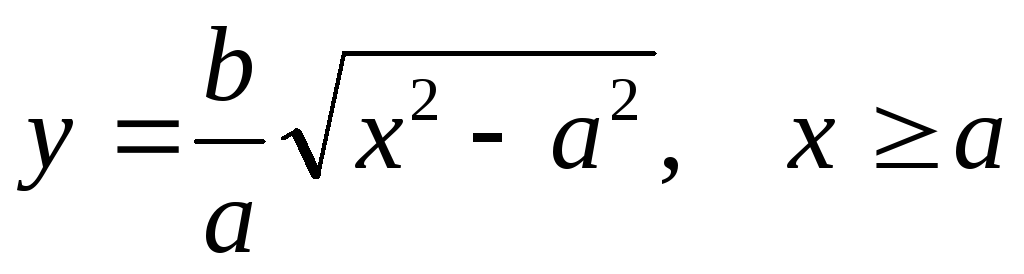
График этой функции неограниченно уходит вправо и вверх и проходит через точку . При этом он очень близко подходит к прямой . Эта прямая называется асимптотой гиперболы. Другой асимптотой гиперболы является прямая .

3. Точки пересечения гиперболы с осью 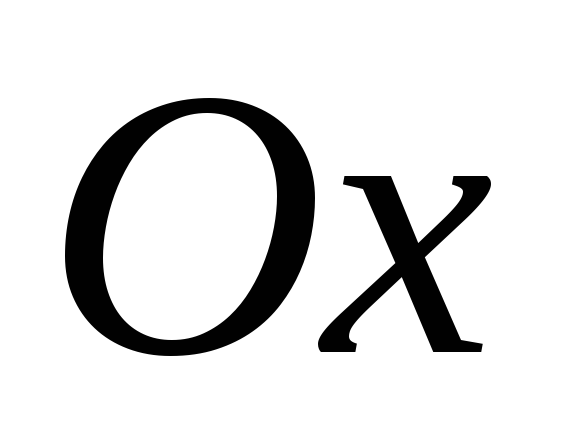– 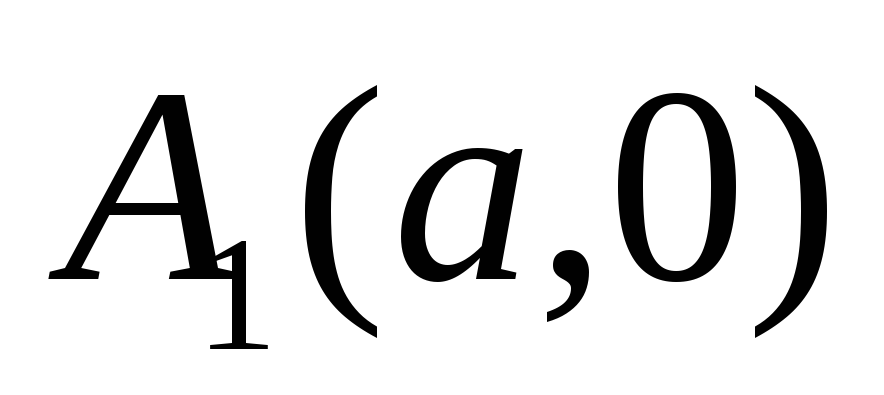и 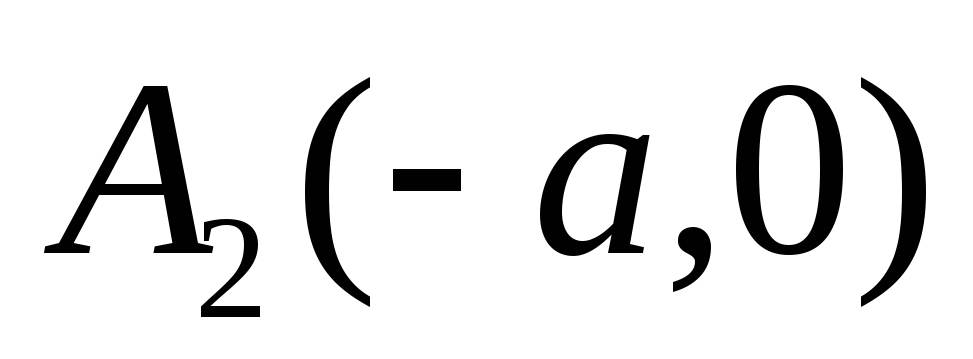- называются ее вершинами; оси симметрии – оси гиперболы, причём ось 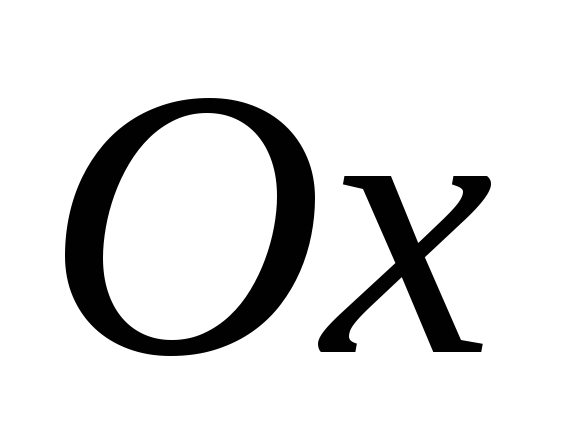– действительная ось, а ось 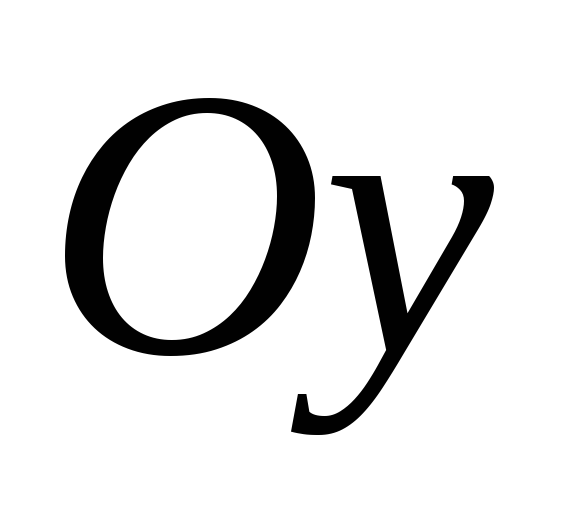– мнимая ось.

4. Величины a и b называются полуосями гиперболы. Если a=b, то гипербола равносторонняя.

5. Если гипербола задана уравнением 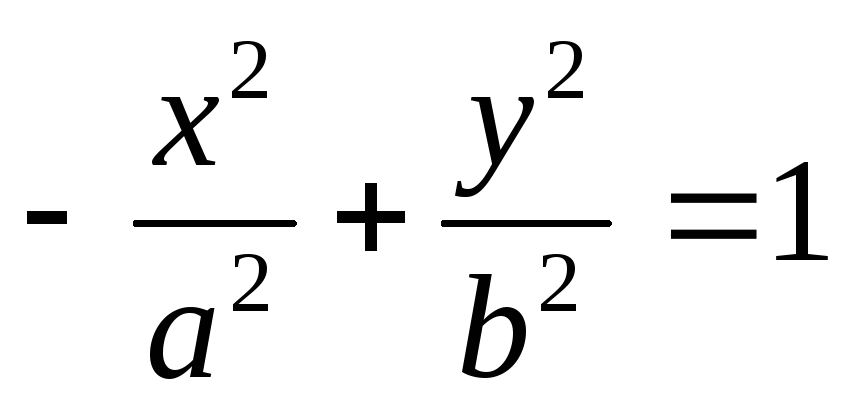, то её фокусы располагаются на оси . Гиперболы, заданные уравнениям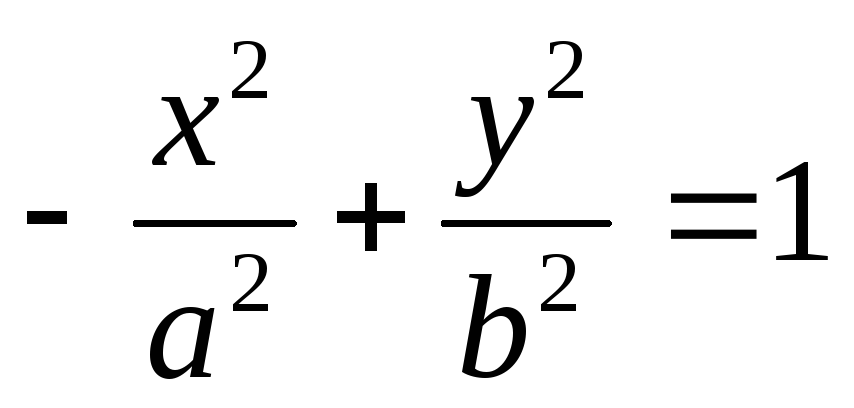и: и 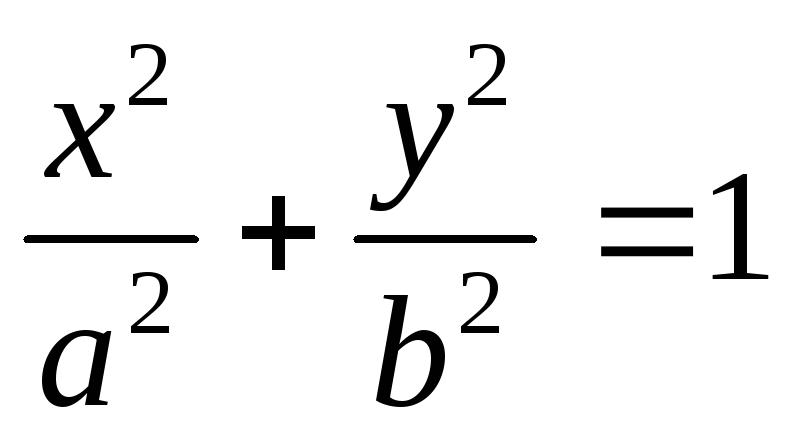, являются сопряжёнными друг с другом.

Определение 10.2. Эксцентриситетом гиперболы называется число, равное отношению фокусного расстояния к действительной оси и обозначается:

Эксцентриситет гиперболы всегда больше 1. Он характеризует форму основного прямоугольника, а значит, и форму гиперболы. Чем меньше эксцентриситет, тем гипербола больше вытягивается вдоль оси Ох. Чем больше эксцентриситет, тем гипербола больше вытягивается вдоль оси Oу.

Определение 10.3. Фокальными радиусами некоторой точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами F₁ и F₂.

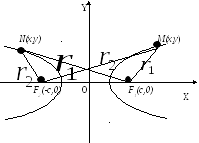Для каждой точки существует два фокальных радиуса. При выводе канонического уравнения гиперболы были вычислены значения фокальных радиусов:

• для точек правой ветви M(x,y)

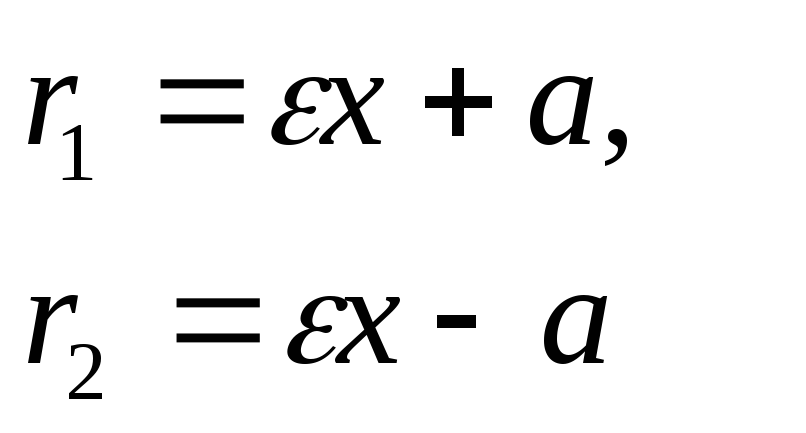
• для точек левой ветви (N(x,y))

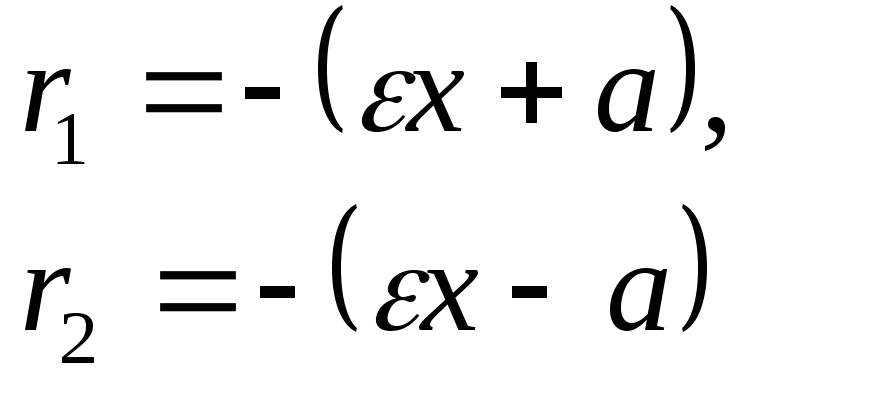
Определение 10.4. Фокальным параметром гиперболы называется длина отрезка перпендикуляра к действительной оси, восстановленного в одном из фокусов до пересечения с гиперболой.

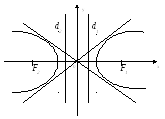
Определение 10.5. Директрисами гиперболы, заданных каноническим уравнением, называются две прямые: .

Так как эксцентриситет гиперболы больше 1, то директрисы гиперболы, параллельные оси Oу, находятся вне гиперболы.

Директриса и фокус считаются соответствующими, если они расположены по одну сторону от центра фигуры.

Теорема 10.6. Отношение расстояний r любой точки М(x, y), принадлежащей гиперболе, до фокуса к её расстоянию до директрисы есть величина постоянная, равная эксцентриситету гиперболы.

Теорема 10.7. Пусть в плоскости заданы точка F и прямая d, не проходящая через точку F. Множество всех точек плоскости, отношение расстояний которых до точки F и расстояний до прямой d есть отличная от единицы величина, равная ε. Множество задаёт эллипс, если и гиперболу, если .

Доказательство:

1. Введём прямоугольную систему координат так, чтобы ось Oу совпадала с d, а ось Ох проходила через F. Тогда .

2. Пусть .

По условию теоремы .

Так как ,

(*)

3. Преобразуем равенство (*):

• возведем обе части в квадрат:

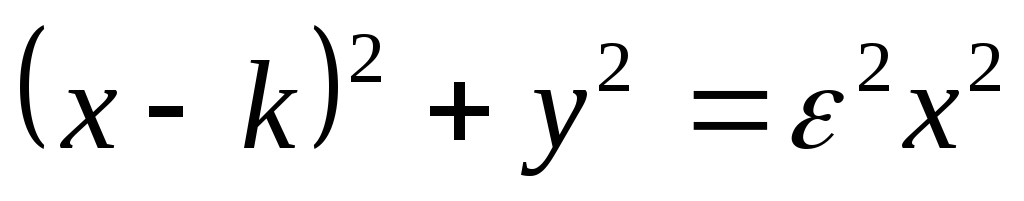
• разделим обе части равенства на :

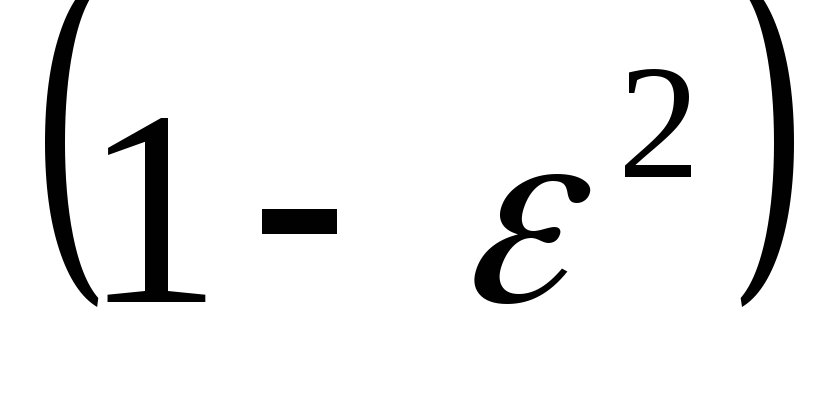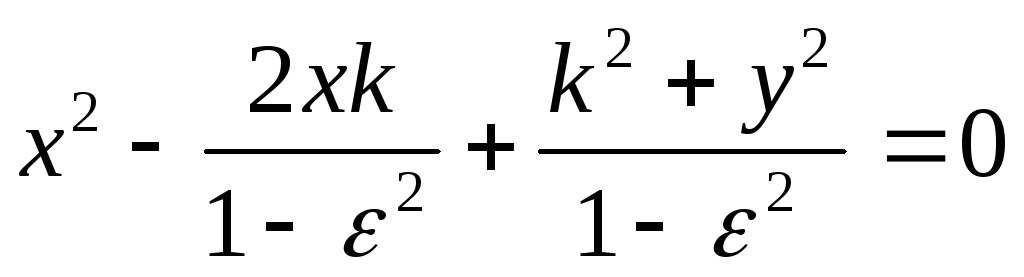
• выделим полный квадрат:

(**)

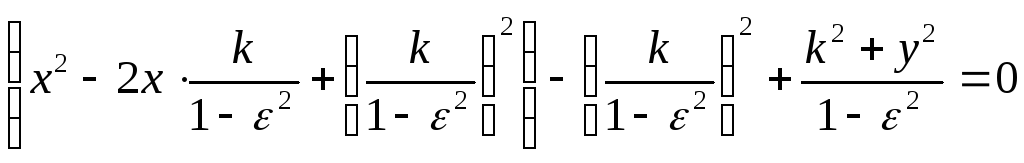
4. Перенесём систему координат параллельным переносом согласно формулам преобразования:

• Выразим х и у из формул преобразования, получим:

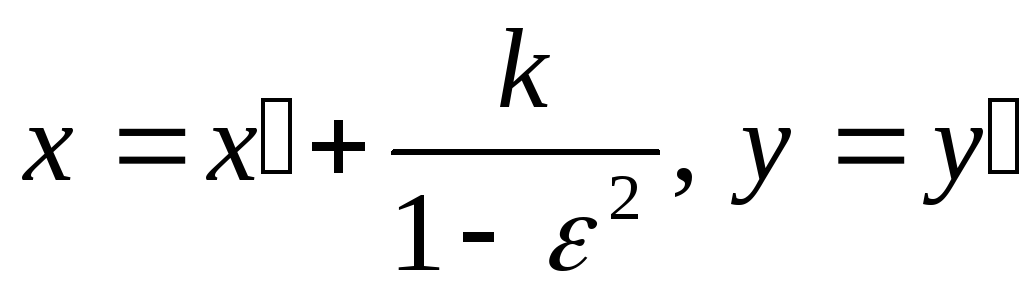
• Подставим вместо 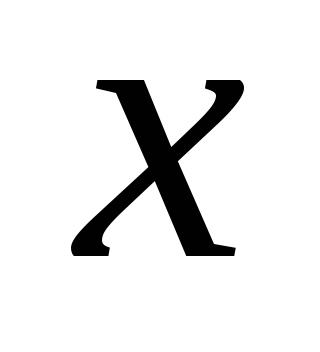и их выражения в уравнение (**) имеем:

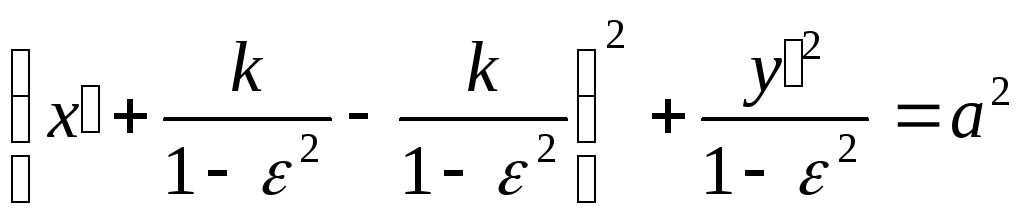, где

• Разделим обе части равенства на :

(***)

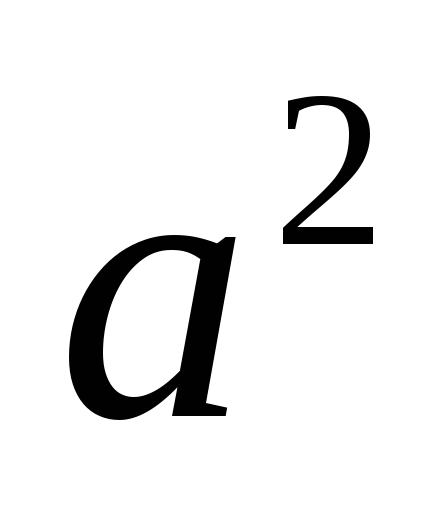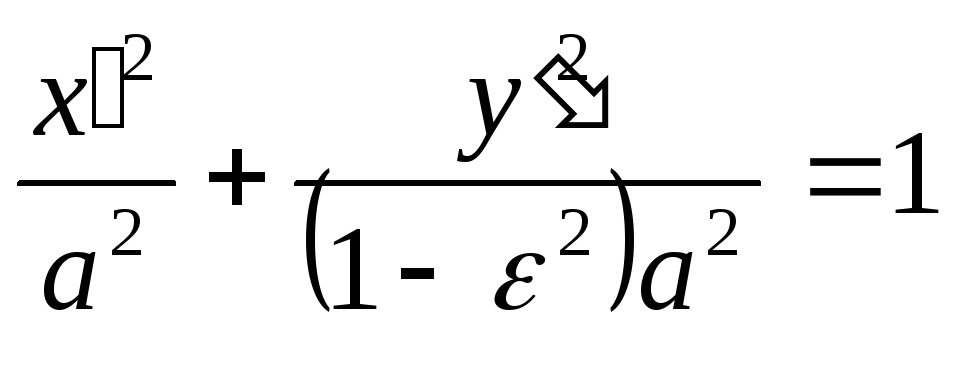
5. Исследуем равенство

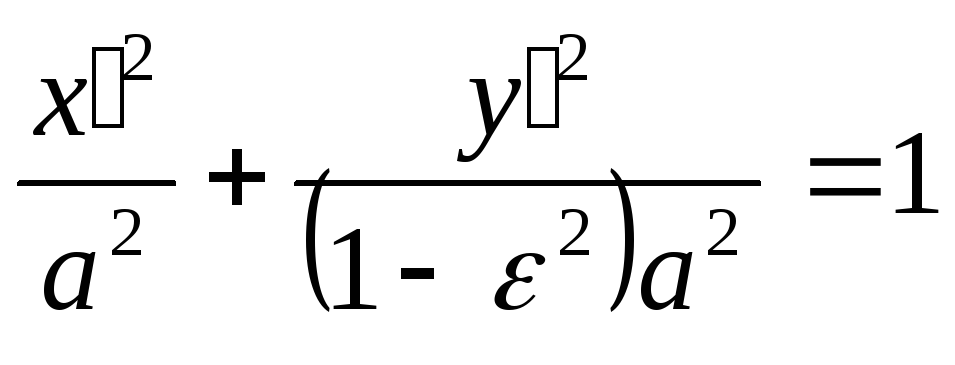
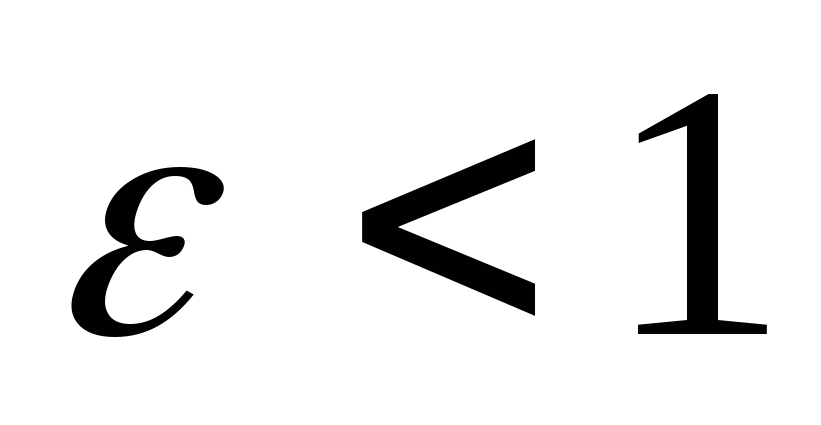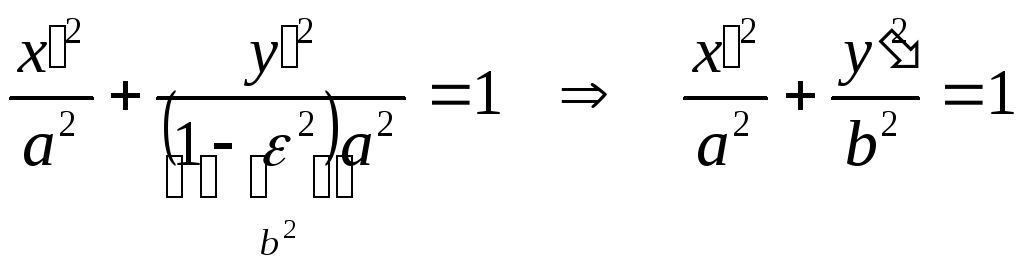• , то - каноническое уравнение эллипса, где 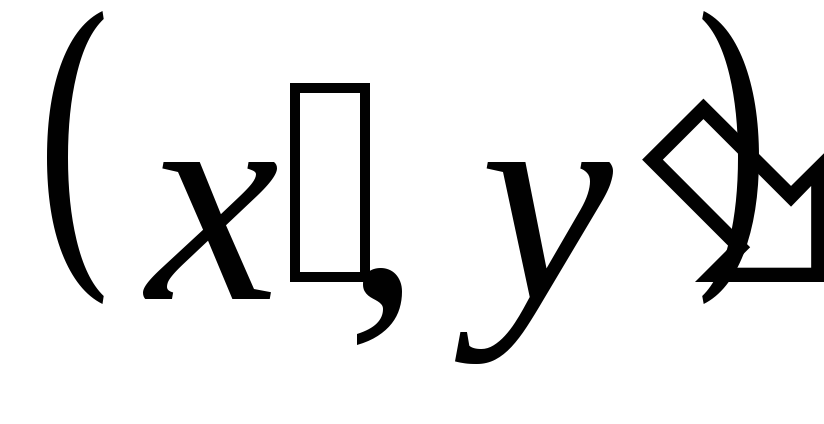- координаты точки М в новой системе координат.

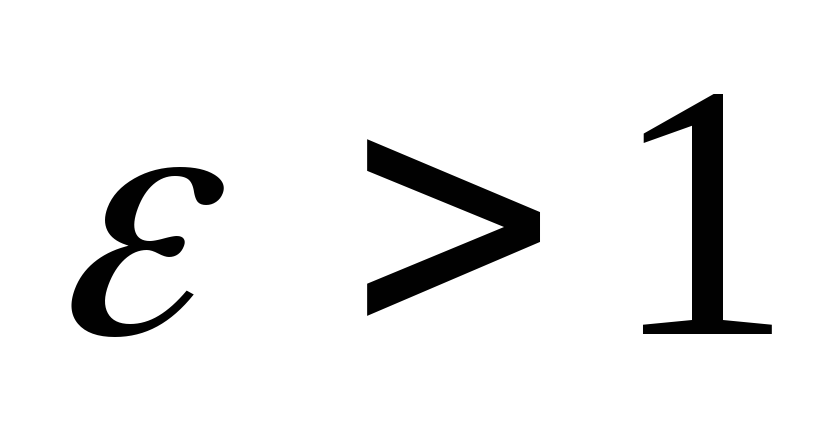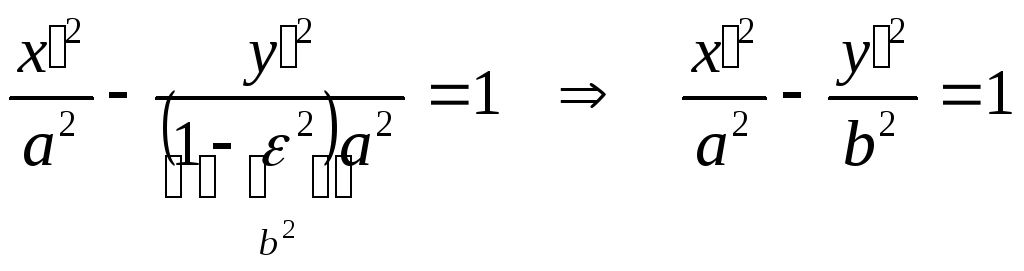• , то - каноническое уравнение гиперболы, где 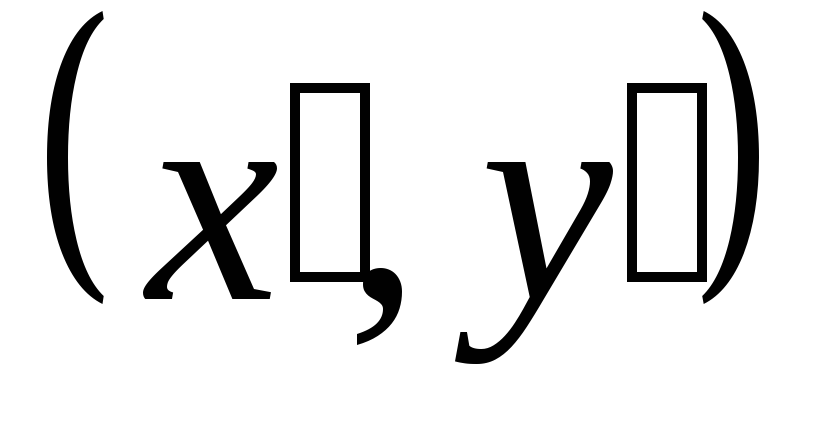- координаты точки М в новой системе координат.

Таким образом, множество всех точек плоскости, отношение расстояний которых до точки F и расстояний до прямой d есть отличная от единицы величина, равная . Множество задаёт эллипс, если и гиперболу, если .

Способы построения гиперболы

Способ №1(в основу положено определение 10.1)

Взять нить произвольной длины и завязать на ней узел в некоторой точке так, чтобы разность отрезков, на которые точка разделила всю нить, равнялась данной величине , меньшей, чем расстояние между фокусами . Концы нити зафиксировать в двух точках – фокусах гиперболы и . Сделав петлю, поставить в нее острием карандаш, удерживая его в вертикальном положении правой рукой, натягивать левой рукой нить за узел , перемещая слегка карандаш, пока нить не будет натянутой. Перемещая карандаш так, чтобы нить все время была натянутой, чертим дугу гиперболы.

Способ №2(в основу положено определение 10.1)

Так как гипербола есть геометрическое место вершин треугольников, имеющих общее основание 2с и постоянную разность двух других сторон 2а, то необходимо построить множество треугольников с общей вершиной по стороне и разности двух других сторон, при этом всякий раз задавая угол .

Способ №3 (в основу положено свойство симметричности гиперболы): построить по точкам часть гиперболы в первой четверти, используя уравнение, а затем использовать симметричность линии относительно осей координат и начала координат.