ВТС 2012 (Новичихин)

Таблица 2 – Минимальные стоимости Cik доставки 1 т груза от поставщиков до пунктов перевалки, включая затраты на перевалку Sk

Таблица 3 – Минимальные стоимости Ckj доставки 1 т груза с пунктов перевалки до потребителей

При определении минимальной стоимости доставки 1 т груза с пунктов перевалки до потребителей должна быть учтена возможность дополнительных перевалок груза в пути следования и стоимость этих перевалок. В этом случае в таблице 3 указываются вид транспорта до пункта перевалки, пункт перевалки и вид транспорта от пункта перевалки, например при доставке груза от П1 до Р3 через пункт перевалки П2 речным и железнодорожным транспортом: рП2ж. Стоимость такой доставки указывается в таблице 3, если она меньше стоимости доставки одним видом транспорта.

3.2 Составление матрицы задачи

Для решения задачи оптимизации распределения перевозок по типу двухэтапной транспортной задачи линейного программирова-

11

ния составляется матрица, в которую из задания на курсовую работу заносятся ресурсы поставщиков аi, потребности потребителей bj и перерабатывающие способности пунктов перевалки qk. Для того чтобы транспортная задача была закрытого типа, должно выполняться следующее условие:

Если сумма ресурсов больше суммы потребностей:

то для преобразования открытой транспортной задачи в задачу закрытого типа вводится столбец фиктивного потребителя PФ, потребности которого равны избытку ресурсов:

Условием двухэтапности транспортной задачи является:

Если условие (9) не выполняется, то задача решается как две обыкновенные (независимые) транспортные задачи.

В качестве показателей оптимальности в правой верхней части клеток матрицы записываются:

−в правой верхней части матрицы – Cij из таблицы 1;

−в левой верхней части матрицы – (Cik+Sk) из таблицы 2;

−в правой нижней части матрицы записываются Ckj из таблицы 3, если выполняется условие:

12

Если же условие (10) не выполняется, в клетке этой части матрицы для исключения недопустимых корреспонденций вместо показателя оптимальности ставят число М (обозначение запрещенной перевозки), значительно превышающее величину Ckj в этих клетках.

Вклетки фиктивной диагонали левой нижней части матрицы в качестве показателей оптимальности записываются нули, в остальные клетки этой части – запрет М.

Если вводится столбец фиктивного потребителя, то показателями оптимальности в верхней части этого столбца являются нули,

внижней – М.

Влевой верхней части клеток матрицы буквой обозначается вид транспорта, которому соответствует минимальное значение показателя оптимальности.

Выполнение условия (10) проверяется сравнением стоимости доставки 1 т груза от каждого поставщика до определенного потребителя через определенный пункт перевалки со стоимостью доставки без перевалки. Поэтому для каждой клетки правой нижней части матрицы записывается m неравенств – по числу поставщиков в узле (в примере m=2). Если хотя бы в одном из них левая часть (стоимость доставки с перевалкой) меньше правой (стоимость доставки

без перевалки), то в соответствующую клетку записывается Ckj. В соответствии с показателями оптимальности матрицы системы неравенств можно записать:

клетка П1 Р1: 36,3 + 0 > 31,3; 25,5 + 0 > 20,5; клетка П1 Р2: 36,3 + 45 > 39,9; 25,5 + 45 > 19,4; клетка П1 Р3: 36,3 + 38 < 75,6; 25,5 + 38 > 55,1; клетка П2 Р1: 43,9 + 46 > 31,3; 23,4 + 46 > 20,5; клетка П2 Р2: 43,9 + 0 > 39,9; 23,4 + 0 > 19,4; клетка П2 Р3: 43,9 + 44 > 75,6; 23,4 + 44 > 55,1; клетка П3 Р1: 50,0 + 58,3 > 31,3; 55,9 + 39 > 20,5; клетка П3 Р2: 50,0 + 37,8 > 39,9; 55,9 + 34 > 19,4; клетка П3 Р3: 50,0 + 35,6 > 75,6; 55,9 + 38 > 55,1.

Всоответствии с этими системами неравенств в клетки правой

нижней части матрицы П1Р3 нужно записать показатели оптимальности соответственно 38,0, а в остальные клетки поставить запрет

М.

13

3.3 Нахождение оптимального плана перевозок

Исходный план рекомендуется составлять способом наименьшего показателя оптимальности (таблица 4). Этим способом заполняются сначала клетки всей правой (верхней и нижней одновременно) части матрицы. Избыток перерабатывающей способности пунктов перевалки заносится в клетки фиктивной диагонали левой нижней части матрицы, а затем способом наименьшего показателя оптимальности заполняются клетки левой верхней части матрицы.

Таблица 4 – Матрица задачи (исходный план)

Сначала необходимо загрузить клетки фиктивного столбца, так как значения показателей оптимальности равны нулю. Загружаем произвольно любую из двух клеток (например, R2РФ) потоком (min из ресурсов R2 или потребностей PФ) xR2РФ=25.

Затем заполняется клетка R2Р2, в которой показатель оптимальности равен 19,4, потоком xR2Р2=175 и т.д. до тех пор, пока не будут удовлетворены потребности всех потребителей.

14

Избыток перерабатывающей способности пунктов перевалки 450, 250 и 75 заносится в клетки фиктивной диагонали левой нижней части матрицы. Далее заполняется левая верхняя часть матрицы.

Число загруженных клеток должно быть равно (m+n–1). План, имеющий число загруженных клеток (m+n–1), является базисным. Согласно доказанной Канторовичем Л.В. теореме, оптимальный план находится среди базисных решений.

Однако, нередки случаи, когда сумма ресурсов равна сумме потребностей не только по матрице в целом, но и по части столбцов и строк, а поэтому число загруженных клеток получается меньше, чем (m+n–1). Для последующих действий надо дополнить число занятых клеток до (m+n–1). Для этого назначаем дополнительные корреспонденции бесконечно малой величины, обозначенные «0».

«Искусственный ноль» вводится в одну из клеток матрицы:

−клетку на пересечении строки, содержащей последнюю заполненную клетку, со столбцом, содержащим признак вырождения;

−клетку на пересечении столбца, содержащего последнюю загруженную клетку, со строкой, содержащей признак вырождения.

В таблице 4 загруженных клеток 9, поэтому необходимо вве-

сти два «искусственных нуля» (в клетки R1П2 и R1П3).

По теореме, доказанной Канторовичем Л.В., условия оптимальности плана формулируются следующим образом:

Допустимый план оптимален тогда и только тогда, когда

каждому поставщику Ri (i=1,2,…,m) и каждому потребителю Pj (j=1,2,…,n) могут быть присвоены некоторые числа Ui и Vj, называемые потенциалами, для которых соблюдаются условия:

Для определения значений потенциалов строк и столбцов из потенциала одной произвольной строки или столбца пользуются равенствами из выражения (12):

V j = cij +U i ; U i =V ij −cij .

15

Начальный потенциал строки или столбца выбирается произвольно, но, чтобы не получить отрицательных потенциалов, рекомендуется принимать его для строчки с наибольшим показателем оптимальности в загруженной клетке.

Задаемся потенциалом первой строки U1=0. Затем по правилу оптимизации определяем остальные потенциалы (через загруженные клетки); например: при U1=0 потенциал V1 определяется:

V1 =U1 +c13 = 0 +50 =50 ;

U 5 =V 3 −c53 =50 −0 =50 и т.д.

После определения всех потенциалов проверяем оптимальность плана по условию (11).

Величиной нарушения будем считать

Наличие хотя бы одного нарушения свидетельствует о том, что проверяемый план не оптимален и должен быть улучшен. Улучшение целесообразно начинать после просмотра всех свободных клеток с клетки, имеющей наибольшее нарушение.

Единственное нарушение равное H31=20,5 имеем в клетке R1PФ. Выявив величину нарушения, вводим поправки в ранее принятый план путем изменения значений xij.

Для этого из выбранной клетки с нарушением проводим замкнутую ломаную линию, двигаясь аналогично ходу шахматной ладьи, при этом изменение движения производим в загруженных клетках на угол 900. Эта линия носит название контура. Там где линия меняет направление, корреспонденции подлежат изменению. Поставим знаки «+» и «–» у вершины контура, начиная с «+» в клетке с нарушением («+» означает, что корреспонденция должна быть увеличена , а «–» – уменьшена).

Величина потока улучшения должна быть равна минимальной корреспонденции со знаком «–», т.е. xул.=min xij(–). Такая корреспонденция у нас в клетке R2PФ=25. Перемещаем эту величину по контуру и получаем новый план (таблица 5), который не имеет нарушений и является оптимальным.

16

Таблица 5 – Результат первой итерации (оптимальный план)

Сокращение затрат на перевозки по оптимальному плану в сравнении с исходным планом:

Затраты на перевозки по исходному плану определяются из выражения (1):

Сисх =36,3 125 +31,3 260 +39,9 85 +19,4 175 +38 125 = =24,212 млн. руб./год.

Затраты на перевозки по оптимальному плану:

Сопт =36,3 125 +31,3 260 +39,9 60 +19,4 200 +38 125 = =23,6995 млн. руб./год.

17

Сокращение затрат на перевозки:

∆С =24,212−23,6995 =0,5125 млн. руб./год.

На основании полученного оптимального плана вычерчивается схема оптимальных транспортных связей (приложение Б).

Библиографический список

1.Правдин, Н. В. Взаимодействие различных видов транспорта:

примеры и расчеты / Н. В. Правдин, В. Я. Негрей, В. А. Подкопаев; под общ. ред. Н. В. Правдина. – М.: Транспорт, 1989. – 208 с.

2.Тихончук, Ю. Н. Рациональное распределение грузовых перевозок между железнодорожным и автомобильным транспорт / Ю. Н. Тихончук, Т. В. Елисеева, А. В. Каяшева. – М.: Транспорт, 1972. – 136 с.

3.Сопоставимые издержки разных видов транспорта при перевозке грузов / под ред. В. И. Дмитриева и К. Н. Шишко. – М.:

Транспорт, 1972. – 488 с.

4.Белов, И. В. Математические методы в планировании на железнодорожном транспорте / И. В. Белов, А. В. Каплан. – М.:

Транспорт, 1972. – 248 с.

18

Приложение А

Расходные ставки при перевозке грузов различными видами транспорта

Расходные ставки при перевозке грузов автотранспортом

19

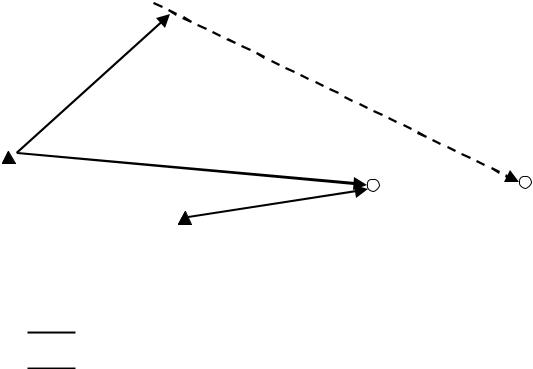
Приложение Б

П1 Р1

110 км /

25 км / 125 тыс. т/год

385 тыс. т/год

200 тыс. т/год

Условные обозначения:

–автомобильные перевозки

–железнодорожные перевозки

Рисунок Б.1 – Пример схемы оптимальных транспортных связей

20