
Spieltheorie_WS1213
.pdf4.5. ANWENDUNGEN |
|
|
|
|
109 |
||
Optimierung von (4.18) f¨uhrt zu |
|
|
|
|
|
||
|
∂Π1 |
= 0 |
x |
= |
a − c |
|
(4.19) |
|
|
|
|||||
|
∂x1 |
1 |
|
2b |
|
||
|
|
|
|
||||
Ein Vergleich mit der Cournot-L¨osung (3.23) zeigt, dass der Stackelberg- F¨uhrer eine gr¨oßere Menge herstellt als in einer statischen Spielsituation. Setzt man das Ergebnis (4.19) in die Reaktionsfunktion (4.16) des StackelbergFolgers ein, so ergibt sich dessen optimale Menge als
x2 = |
a − c |
, |
(4.20) |
|
4b |
||||
|
|
|
was weniger ist als die Menge in einem Cournot-Duopol. Das ist auch genau der Grund f¨ur die Verhaltensweise des Stackelberg-Folgers: Da dieser weiß, dass der Stackelberg-Folger eine negativ geneigte Reaktionsfunktion hat, kann er seine Menge gegen¨uber der Cournot-L¨osung erh¨ohen. Die Mengen sind also strategische Substitute in diesem Modell.
Die Addition der Marktmengen liefert
x = x1 + x2 = |
3 (a − c) |
, |
(4.21) |
|
4b |
||||
|
|
|
was mehr ist als die Marktmenge in der Cournot-L¨osung (3.24). Entlang einer negativ geneigten Nachfragefunktion muss der Preis niedriger sein.
Daraus l¨asst sich auch sofort etwas zum Einfluss der dynamischen Spielstruktur auf die Gewinne der beiden Konkurrenten sagen: Insgesamt sinkt die Gewinnsumme, da schon in der Cournot-L¨osung eine h¨ohere als die Monopolmenge produziert wird, man sich also auf dem fallenden Ast der Gewinnfunktion bewegt – und sich entlang dieses Astes durch eine weitere Ausweitung der Menge weiter nach unten bewegt. Allerdings ist die Inzidenz auf die Gewinne sehr unterschiedlich: Der Stackelberg-F¨uhrer gewinnt gegen¨uber der Cournot- L¨osung, da er ja diese auch durchsetzen k¨onnte – der Stackelberg-Folger wird ja immer einen Punkt auf seiner Reaktionsfunktion w¨ahlen –, dieses aber nicht tut. Damit ist klar, dass sein Gewinn steigen muss. Nimmt man die Resultate f¨ur den Gewinn des Stackelberg-F¨uhrers und f¨ur die Gewinnsumme zusammen, so folgt, dass der Gewinn f¨ur den Stackelberg-Folger eindeutig sinken muss.
Tabelle 4.2 fasst die qualitativen Ergebnisse zusammen.
4.5.2Geldpolitik II: Stackelberg-F¨uhrerschaft der Lohnsetzer im Barro-Gordon-Modell
In diesem und dem n¨achsten Abschnitt werfen wir einen genaueren Blick auf das Barro-Gordon-Modell zur Analyse der Geldpolitik, das wir in seiner Grundstruktur bereits in Abschnitt 3.7.4 auf Seite 77 kennen gelernt hatten.
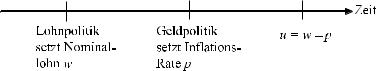
110 |
|
|
KAPITEL 4. NICHTKOOPERATIVE SPIELE II |
|||||
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x1 + x2 |
p |
Π1 |
Π2 |
Π1 + Π2 |
|
|
↑ |
↓ |
↑ |
↓ |
↑ |
↓ |
↓ |
|
|
|
|
|
|
|
|
|
|
Tabelle 4.2: Der qualitative Einfluss der dynamischen Struktur im StackelbergDuopol
Anbieter 1 ist Stackelberg-F¨uhrer, Anbieter ist Stackelberg-Folger. Die Pfeile geben die Ver¨anderung der Gr¨oße relativ zur Cournot-L¨osung an.
Zun¨achst geht es um die Konsequenzen einer dynamischen Struktur des Spiels zwischen privatem Sektor und geldpolitischen Akteuren
– und insbesondere um die Implikationen und die W¨unschbarkeit einer mehr oder weniger an der Bek¨ampfung von Inflation ausgerichteten Geldpolitik.1
In Abschnitt 3.7.4 auf Seite 77 war der private Sektor dabei sehr rudiment¨ar dadurch abgebildet, dass dieser systematisch falsche Inflationserwartungen vermeiden wollte. Hier wird nun dem privaten Sektor etwas mehr Struktur gegeben.2 Konkret wird unterstellt, dass neben der Geldpolitik die Lohnpolitik der zweite zentrale Spieler auf der makro¨okonomischen Ebene ist. Diese setzt den Nominallohn. Der logarithmierte Wert des Nominallohns wird im Folgenden mit w bezeichnet.
Das makro¨okonomische Ergebnis h¨angt dann sowohl vom Verhalten der Geldpolitik, die die Inflationsrate weiterhin direkt bestimmen kann, als auch von der Lohnpolitik ab. Weiterhin wird angenommen, dass die Lohnsetzer zeitlich bzw. logisch vor der Geldpolitik ihre Entscheidung fixieren k¨onnen und damit in der Position eines Stackelberg-F¨uhrers sind. Entsprechend agiert die Geldpolitik als Stackelberg-Folger. Abbildung 4.17 zeigt diese zeitliche Abfolge.
Abbildung 4.17: Timing im Stackelberg-Modell des Spiels zwischen Lohnund Geldpolitik.
|
Auf der ”dritten Stufe” in Abbildung 4.17 ist keine eigentliche Entschei- |
|
|
|
|
1 |
¨ |
|
|
Alle Uberlegungen hier beziehen sich nur auf Gleichgewichtsph¨anomene, d.h. nicht auf |
|
die Frage, inwiefern die Geldpolitik konjunkturelle Schwankungen ausgleichen kann oder sollte. Dieser Aspekt – der in der geldpolitischen Literatur sehr prominent ist – w¨urde sich zwar mehr oder weniger problemlos ber¨ucksichtigen lassen, ¨andert aber nichts Wesentliches an der hier zu analysierenden Interaktion.
2Die Modellierung st¨utzt sich auf Jerger (2002a) und Jerger (2002b).

4.5. ANWENDUNGEN |
111 |
dung zu tre en; hier werden vielmehr die Konsequenzen der vorangegangenen Entscheidungen der Akteure f¨ur die interessierenden Variablen berechnet und angegeben. Im vorliegenden Fall ist dies einfach die H¨ohe der Arbeitslosenquote u, die als proportional zum (Logarithmus des) Reallohn(s) w − p angenommen wird:3
u = w − p |
(4.22) |
¨
Okonomisch steckt dahinter letztlich eine fallende Arbeitsnachfragekurve; dass die Elastizit¨at hier auf den Wert 1 normiert wird, ist f¨ur die folgende Argumentation unwichtig, d.h. erleichtert nur die Notation des Modells.
Die Nutzenfunktionen der Akteure sind wie folgt beschrieben. Die Geldpolitik minimiert die Verlustfunktion
LG = u2 + αp2 mit α ≥ 0. |
(4.23) |
Diese Nutzenfunktion ist v¨ollig isomorph zu (3.37); es wurde lediglich als Maß f¨ur den Auslastungsgrad der Volkswirtschaft anstelle der Abweichung von Output und Zieloutput die Arbeitslosenquote verwendet und deren Zielwert auf Null normiert. α ist ein Maß f¨ur das relative Gewicht von Inflationsziel bzw. realem Ziel. α = 0 bildet die Situation einer Zentralbank ab, die sich uberhaupt¨ nicht um Inflation k¨ummert, sondern sich ausschließlich dem Outputziel verpflichtet sieht.
Die Lohnsetzer weisen eine ¨ahnliche Nutzenbzw. Verlustfunktion auf,
n¨amlich |
|
LW = u2 + βp2 − 2χ (w − p) mit β, χ ≥ 0. |
(4.24) |
Auch diese Gruppe ist an einer niedrigen Arbeitslosenquote interessiert. F¨ur β > 0 l¨asst sich auch eine Inflationsaversion der Lohnsetzer einfangen, der Parameter χ bildet dar¨uber hinaus ein Reallohnziel ab; da die Lohnsetzer plausiblerweise an einem hohen Reallohn interessiert sind, geht dieser negativ in die Verlustfunktion ein.
Wieder wird die Methode der R¨uckw¨artsinduktion angewandt, d.h. zun¨achst wird das Kalk¨ul der Zentralbank betrachtet.
Einsetzen von (4.22) in (4.23) liefert die Schreibweise
LG = (w − p)2 + αp2, |
(4.25) |
3In einem one-shot game, wie es hier vorliegt, k¨onnen wir p sowohl f¨ur den Log des Preisniveaus als auch f¨ur die Inflationsrate verwenden. Dies folgt aus der Tatsache, dass πt = pt − pt−1. Bei Normierung des (exogenen) Preisniveaus der Vorperiode auf Pt−1 = 1 pt−1 = 0 folgt daraus, dass πt = pt. P bezeichnet dabei das nicht logarithmierte Preisniveau. Die Zeitindizierung f¨allt in der Darstellung im Text weg, da diese in einem one-shot-Kontext nicht von Bedeutung ist.

112 |
|
KAPITEL 4. NICHTKOOPERATIVE SPIELE II |
|||
deren Minimierung uber¨ p das folgende Resultat liefert: |
|
|
|||
|
∂LG |
= −2 (w − p) + 2αp = 0 p = |
|
w |
(4.26) |
|
∂p |
1 + α |
|||
|
|
|
|||
Diese Gleichung kann als geldpolitische Reaktionsfunktion aufgefasst werden. Eine ausschließlich auf das reale Ziel fixierte Geldpolitik (α = 0) wird einfach p = w setzen und damit gem¨aß (4.22) immer u = 0, d.h. Vollbesch¨aftigung erreichen k¨onnen. Hingegen wird ein ”inflation nutter” (α → ∞) uber¨- haupt nicht auf ein h¨oheres Niveau der Nominall¨ohne reagieren, damit das Inflationsziel (p = 0) in jedem Fall erreicht wird.1 Algebraisch ausgedr¨uckt:
lim |
∂p |
= 0. |
(4.27) |
|
|||
α→∞ ∂w |
|
|
|
Der n¨achste Schritt besteht nun in der Ermittlung des optimalen Verhaltens der Lohnsetzer. Hierzu ist das Verhalten der Geldpolitik (4.26) sowie die die Bestimmungsgleichung f¨ur u (4.22) in die Verlustfunktion der Lohnsetzer (4.24)
einzusetzen. Dies f¨uhrt zu |
|
+ β |
|
1 + α |
− 2χ |
1 + α.2 |
(4.28) |
|||||||
|
|
|
LW = |
1 + α |
||||||||||
|
|
|
|
|
αw |
2 |
|
|
w |
2 |
|
αw |
|
|
Minimierung dieser Verlustfunktion uber¨ w liefert |
|
|
|
|||||||||||
|
∂w |
= 2 |
1 + α |
1 + α + 2β |
1 + α |
1 + α − 2χ1 + α = 0 |
(4.29) |
|||||||
|
∂LW |
|
αw |
|
α |
|
|
|
w |
1 |
|
|
α |
|
w = χα (1 + α)
β + α2
Gleichung (4.29) gibt den Nominallohn in Kategorien der Pr¨aferenzparameter der Akteure an, ist also keine Reaktionsfunktion, sondern bereits die ”Schlussgleichung” f¨ur diese Variable. Einsetzen von (4.29) in die geldpolitische Reaktionsfunktion (4.26) liefert die L¨osung des Modells f¨ur die Inflationsrate
p = |
|
χα |
|
||
|
|
. |
(4.30) |
||
β + α2 |
|||||
Die L¨osung f¨ur die Arbeitslosenquote ergibt sich als |
|
||||
u = |
|
χα2 |
|
(4.31) |
|
|
β + α2 |
||||
Halten wir zun¨achst die folgenden Ergebnisse fest:
1”Nicht reagieren” bezieht sich hier auf die angenommene Handlungsvariable p. Wird nicht p, sondern ein Zins oder Geldmengenaggregat als Handlungsparameter aufgefasst, so liegt es auf der Hand, dass durchaus eine Reaktion erfolgt – und sogar eine denkbar extreme: Jeder inflation¨are Druck, der von noch so hohen Nominallohnabschl¨ussen kommt wird durch eine Politik des ”leaning against the wind” in ihren Inflationswirkungen bek¨ampft.
2Dabei wird die aus 4.26 folgende Tatsache benutzt, dass w − p = 1+αwα .

4.5. ANWENDUNGEN |
113 |
• Je h¨oher das Gewicht χ des Reallohns in der Verlustfunktion der Lohnsetzer ist, desto h¨oher sind sowohl Inflation als auch Arbeitslosenquo-
te im Stackelberg-Gleichgewicht des Modells: |
∂p |
4.30 |
= |
α |
|
> |
0 und |
|||
∂χ |
β+α |
2 |
||||||||
∂u |
|
α2 |
|
|
|
|||||
|
= |
|
> 0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
∂χ |
4.30 |
β+α |
|
|
|
|
|
|
|
|
•Weisen auch die Lohnsetzer ein gewisses Maß an Inflationsaversion auf (β > 0), so wirkt dies sowohl auf die Inflationsrate als auch auf die Arbeitslosenquote senkend. Anders gesagt: Agieren die Lohnsetzer ohne R¨ucksicht auf die Inflationsrate, so f¨uhrt dies zu einem gesamtwirtschaftlich eindeutig schlechteren Gleichgewicht.1
Die zwei zentralen Implikationen des Modells sind jedoch die Folgenden: Zum einen ist die gleichgewichtige Arbeitslosenquote umso gr¨oßer, je konservativer die Zentralbank ist:
∂α 4.31 |
= |
β + α2 |
|
2 |
2αχ α2 + β |
− 2αα2χ = 2αβχ β + α2 |
|
> 0 |
||
∂u |
|
|
1 |
|
|
|
|
1 |
|
|
(4.32) Dies ist insofern ein sehr wichtiges Resultat, als eine systematisch weniger inflationsaverse Geldpolitik in diesem Modell tats¨achlich zu einer Reduktion der Arbeitslosenquote f¨uhrt. In diesem Sinn liegt eine jenseits des konjunkturellen Horizonts relevante Nichtneutralit¨at der Geldpolitik vor, die in dem Modell des Abschnitts 3.7.4 auf Seite 77 nicht enthalten war. Es wird gleich gezeigt werden, dass dieser qualitative Unterschied auf das Zusammenwirken zweier wesentlicher Modifikationen beruht, der dynamischen (Stackelberg-) Struktur des Spiels einerseits und der Eigenschaft der Inflationsaversion von Lohnsetzern andererseits. Die Bedeutung der Inflationsaversion der Lohnsetzer kann
unmittelbar aus 4.32 abgelesen werden. Es gilt n¨amlich, dass
∂u
= 0. (4.33)
∂α 4.31 β=0
Zum anderen kann man zeigen, dass die Inflationsrate eine im Allgemeinen nicht-monotone Funktion der Zentralbankkonservativit¨at ist – es also einen Bereich gibt, in dem eine st¨arkere Inflationsaversion der geldpolitischen Akteure zu weniger bzw. zu mehr Inflation im Gleichgewicht f¨uhrt. Dieser Punkt soll zun¨achst formal gezeigt werden. Aus (4.30) l¨asst sich sofort ableiten, dass
∂p |
|
= |
1 |
2 |
|
χ β − α2 |
= 0 |
f¨ur α2 |
= β |
(4.34) |
|
∂α |
4.30 |
|
|
2 |
|
|
> 0 |
f¨ur α2 |
< β |
|
|
β + α |
|
< 0 |
f¨ur α2 |
> β |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1Das ist stringent zu zeigen, wenn die gesellschaftliche Verlustfunktion LG durch Einsetzen der Modell¨osung (4.30) und (4.31) als Funktion aller Pr¨aferenzparameter berechnet wird. Tut man dies, so ergibt sich, dass ∂L∂βG < 0, d.h. der gesellschaftliche Verlust ist um so geringer, je h¨oher die Sensibilit¨at der Lohnsetzer f¨ur die Inflationsrate ist.

114 KAPITEL 4. NICHTKOOPERATIVE SPIELE II
In Prosa: Ausgehend von einer sehr populistischen Zentralbank (kleines α) wird durch die Etablierung einer st¨arker am Inflationsziel interessierten Geldpolitik die gleichgewichtige Inflationsrate paradoxerweise erh¨oht!
Insbesondere gilt, dass sowohl eine ultrapopulistische Zentralbank (α = 0) als auch eine ultrakonservative Zentralbank (α → ∞) f¨ur eine Inflationsrate
von Null sorgen: |
χ |
|
|
|
lim p = lim p = lim |
= 0. |
(4.35) |
||
|
||||
α→0 α→∞ α→∞ 2α |
|
|
||
Bei der Berechnung des Limes f¨ur α → ∞ in (4.35) wurde die Regel von De L‘Hˆopital verwendet.
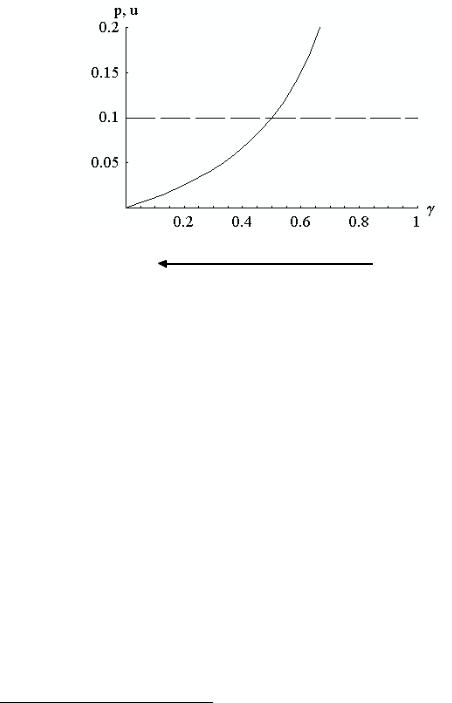
Abbildung 4.18 zeigt die qualitativen Eigenschaften der L¨osung mit Hilfe einer numerischen Simulation. Entlang der horizontalen Achse wird der Grad der Zentralbankkonservativit¨at variiert, wobei die Variation von α zwischen Null und Unendlich durch die Definition der Hilfsvariabeln γ = 1/(1 + α) auf den Bereich zwischen Null und 1 abgebildet wird.
Abbildung 4.18: Die qualitativen Eigenschaften eines StackelbergGleichgewichts bei inflationsaversen Lohnsetzern.
Man sieht, dass das makro¨okonomisch beste Resultat (p = u = 0) durch eine ultrapopulistische Zentralbank herbeigef¨uhrt wird. Die Intuition hinter diesem Ergebnis lautet wie folgt: Wenn die Geldpolitik sich ausschließlich auf das reale Ziel konzentriert, kann sie dies aufgrund ihrer Position als StackelbergFolger immer tun: Was immer an Nominall¨ohnen in der ersten Stufe gesetzt wurde, muss nur – und kann auch – durch eine entsprechende Inflation real ”unsch¨adlich” gemacht werden. Da die Lohnsetzer dieses Verhalten nat¨urlich antizipieren ist ihnen im Grunde klar, dass sie keinerlei Einfluss auf alle realen Variablen haben, konkret: auf Arbeitslosenquote und Reallohn. F¨ur α = 0 gilt

4.5. ANWENDUNGEN |
115 |
diese Machtlosigkeit bzgl. der realen Variablen unabh¨angig von der Intensit¨at des Reallohnziels χ. Wenn nun die Lohnsetzer auch nur einen geringen Grad an Inflationsaversion mitbringen, so sehen sie in der ersten Stufe, dass sie im Prinzip nur Einfluss auf die Inflationsrate haben. Ihr Rationalit¨atskalk¨ul diktiert ihnen dann sich ausschließlich auf dieses Ziel zu konzentrieren und damit der Zentralbank in der zweiten Stufe Bedingungen zu bescheren, die es ihr erlaubt, das reale Ziel ohne inflation¨are Nebenwirkungen zu erreichen.1 Diese Logik macht auch klar, warum und wie die hier unterstellte sequentielle Struktur des Spiels von Bedeutung ist.
Das Ergebnis ist denkbar weit entfernt vom Resultat des Modells in Abschnitt 3.7.4 auf Seite 77. Dort wurde ja gezeigt, dass die Zentralbank in einem Gleichgewicht mit Rationalen Erwartungen keinerlei Einfluss auf die realen Variablen hat und daher so konservativ wie m¨oglich sein sollte.
Die Bedeutung der sequentiellen Struktur wird genauer herausgestellt, indem nun dieses Ergebnis innerhalb des extrem einfachen Modellrahmens in diesem Abschnitt ”reproduziert” wird. D.h. im Rest dieses Abschnitts wird noch das Nash-Gleichgewicht des statischen Spiels berechnet.
Die geldpolitische Reaktionsfunktion (4.26) kann dabei einfach ubernom¨- men werden, das lohnpolitische Verhalten muss aber neu abgebildet werden; die Lohnsetzer wissen ja in einem statischen Kontext, dass die geldpolitischen Akteure nicht von einem spezifischen Wert von w ausgehen, sondern allgemein nur von lohnpolitischem Optimalverhalten. Die zu optimierende Verlustfunktion der Lohnsetzer muss also in einer Form geschrieben werden, die noch konditional auf p ist. Einsetzen von (4.22) in (4.24) liefert
LW = (w − p)2 + βp2 − 2χ (w − p) , |
(4.36) |
woraus sich sofort die lohnpolitische Reaktionsfunktion wie folgt ableiten l¨asst.
∂LW |
= 2 (w − p) − 2χ = 0 w = p + χ |
(4.37) |
|
∂w |
|||
|
|
Einsetzen von (4.37) in (4.26) liefert die gleichgewichtige Inflationsrate als
p = |
χ |
(4.38) |
α |
(4.37) und (4.26) determinieren gem¨aß (4.22) die Arbeitslosenquote im
Gleichgewicht als |
|
u = χ. |
(4.39) |
Die Inflationsrate (4.38) ist in diesem Szenario eine monotone Funktion der Konservativit¨at der Zentralbank, w¨ahrend die Geldpolitik nun die realen Variablen nicht beeinflusst. Vielmehr ist die Arbeitslosenquote im Gleichgewicht proportional zur Gewichtung des Reallohnziels in der Zielfunktion der Lohnsetzer.
1Formal: Aus (4.29) folgt, dass w|α=0 = 0.
116 |
KAPITEL 4. NICHTKOOPERATIVE SPIELE II |
Abbildung 4.19 auf der n¨achsten Seite zeigt die qualitativen Eigenschaften der Nash-L¨osung des statischen Spiels wieder in einer numerischen Simulation. Alle Parameter sind dabei genau so gew¨ahlt wie f¨ur die Simulation des sequentiellen Spiels in Abbildung 4.18 auf der vorherigen Seite.
p
u
? ? ? |
? ? 0 |
|
Zunehmende Konservativität |
|
der Geldpolitik |
Abbildung 4.19: Die qualitativen Eigenschaften eines Nash-Gleichgewichts im statischen Spiel zwischen Lohnsetzern und Geldpolitik.
Nat¨urlich resultiert nun wieder die normative Implikation, dass sich die Geldpolitik m¨oglichst konservativ verhalten sollte, d.h. einen ausschließlichen Fokus auf das Inflationsziel legen sollte.
Eine wichtige Lehre aus dem Vergleich des sequentiellen und statischen Spiels in diesem Abschnitt ist vor allem, dass die Unterschiedlichkeit der L¨osungen in beiden Szenarien von der genauen Spezifikation des Modells abh¨angt. So w¨aren in dem Modell dieses Abschnitts die Ergebnisse im statischen und dynamischen Spiel identisch, wenn es keine Inflationsaversion der Lohnsetzer g¨abe (d.h. f¨ur β = 0).1
4.5.3Geldpolitik III: Reputation im Barro-Gordon-Modell
In diesem Abschnitt werden nun die Unterschiede zwischen statischem und dynamischem Spiel wieder in den Hintergrund geschoben und die Frage nach der M¨oglichkeit eines Reputationsaufbaus der geldpolitischen Akteure gestellt. Dabei wird die Modellstruktur des Abschnitts 3.7.4 auf Seite 77 wieder unterstellt, d.h. die geldpolitische Zielfunktion ist wieder durch
1In der Tat wird in dem Lehrbuch von Gibbons (1992) das traditionelle Barro-Gordon- Modell (vgl. Abschnitt 3.7.4 auf Seite 77 explizit als dynamisches Spiel pr¨asentiert.
4.5. ANWENDUNGEN |
|
|
|
117 |
LG = −uG = απ2 + (y − y˜)2 |
(4.40) |
|||
gegeben, die Phillipskurve y = y |
N |
e |
|
¨ |
|
+ β (π − π |
) ist das ”Modell der Okono- |
||
mie”, wobei die Beziehung zwischen dem inflationsstabilen Outputniveau yN und dem Zielniveau der Geldpolitik y˜ gegeben ist durch y˜ = γ · yN mit γ > 1.
Unter der Annahme Rationaler Erwartungsbildung π = πe resultieren im
Nash-Gleichgewicht die Inflationsrate |
|
|||
π = |
|
(γ − 1) β |
yN |
(4.41) |
|
|
|||
|
|
α |
|
|
und das Outputniveau |
|
|
|
|
|
y = yN . |
(4.42) |
||
Wie bereits diskutiert, weist diese L¨osung eine Ine zienz in Form einer unerw¨unscht hohen Inflationsrate auf, die im Gleichgewicht nicht in der Lage ist, das Niveau der realen Aktivit¨at zu steigern. Es w¨are daher vorstellbar, dass sich die Geldpolitik in dieser Situation eine Reputation aufbauen m¨ochte, die Inflationsrate bei Null zu halten. Wenn dies auch von den Privaten erwartet wird, so andert¨ sich nichts am Outputniveau 4.42, die Inflationsrate ginge jedoch auf Null zur¨uck. Reputationsaufbau w¨are also eine denkbare L¨osung des Zeitinkonsistenzproblems der Geldpolitik. Allerdings h¨atte in dieser Situation die Geldpolitik einen Anreiz, eine h¨ohere Inflationsrate zu kreieren – was ja genau der Kern des Zeitinkonsistenzproblems ist. Nachfolgend wird nun zun¨achst der Fall eines endlich wiederholten Spiels betrachtet, danach die Situation bei unendlicher Wiederholung.
Endlich wiederholte Interaktion
Wenn das oben noch einmal kurz beschriebene one-shot game aus Abschnitt 3.7.4 auf Seite 77 f¨ur eine vorgegebene Zahl von T Perioden gespielt wird, so l¨asst sich die teilspielperfekte Abfolge der gleichgewichtigen L¨osungen der T Teilspiele durch R¨uckw¨artsinduktion ermitteln.
Das Teilspiel in Periode T besteht nur noch aus dem one-shot game in dieser Periode. Die Anreize der Akteure h¨angen dabei in keiner Weise von der Geschichte des Spiels ab – womit klar ist, dass hier kein Weg an der ine zienten L¨osung (4.41) und (4.42) vorbei f¨uhrt. Anders gesagt: Die Zentralbank w¨urde bei Inflationserwartungen in H¨ohe von πTe = 0 eine Inflationsrate πT > πTe = 0 w¨ahlen. Daher ist πTe = 0 kein Gleichgewicht, da der private Sektor den Anreiz der Zentralbank und somit die zeitkonsistenten Inflationserwartungen bildet.
In Periode T ergibt sich also πT = |
(γ−1)β |
y |
N |
und yT = y |
N |
. |
α |
|
|
||||
|
|
|
|
|
|
In Periode T −1 besteht das Teilspiel aus den Stufenspielen der Perioden T und T −1. Damit ist klar, dass in T eine in T −1 evtl. aufzubauende Reputation nichts n¨utzt, da sich auch bei πT −1 = 0 an der im letzten Absatz geschilderten

118 |
KAPITEL 4. NICHTKOOPERATIVE SPIELE II |
|||
Logik nichts andert¨ |
. Ein Reputationsaufbau ist somit unglaubw¨urdig und un- |
|||
terbleibt deswegen. Das Ergebnis besteht ist also auch hier πT −1 = |
(γ−1)β |
y |
N |
|
α |
|
|||
und yT −1 = yN .
In Periode T − 2 ist die Logik nun v¨ollig parallel zu der in T − 1, d.h. ein Reputationsaufbau ist unn¨utz, ergo unglaubw¨urdig und unterbleibt daher. Die Logik ¨andert sich nat¨urlich auch nicht f¨ur noch gr¨oßer Teilspiele, die weiter zur¨uckreichen.
Damit ist gezeigt, dass ein Reputationsaufbau in einer endlich wiederholten Spielsituation nicht auftritt. Dies ist eine Anwendung des Theorems in Abschnitt 4.4.2 auf Seite 95, das ja behauptete, dass sich ein eindeutiges NashGleichgewicht in einem one-shot game bei endlicher Wiederholung dieser Situation einfach perpetuiert.
Unendlich wiederholte Interaktion
Auch sehr stabile Institutionen leben nicht unendlich lange, dennoch ist gerade in der Geldpolitik die Unterscheidung zwischen endlichem und unendlichem Zeithorizont von großer Bedeutung. Denn in einer zun¨achst einmal ”nat¨urlichen” Situation, in der Geldpolitik von einer gew¨ahlten Regierung betrieben wird, wechselt diese – jedenfalls potentiell – nach Ablauf einer Legislaturperiode. Diese dauern typischerweise ca. 4-5 Jahre und bieten damit eine wirklich begrenzte zeitliche Perspektive, die mit der Logik eines endlich wiederholten Spiels gut abgebildet ist. Eine nicht von der Regierung abh¨angige Zentralbank bzw. eine Zentralbank, die f¨ur die Mitglieder der Entscheidungsgremien l¨angere Amtszeiten vorsieht, kann dagegen schon eher eine Kontinuit¨at gew¨ahrleisten, die durch ein unendlich wiederholtes Spiel besser abgebildet ist.
Nachfolgend wird nun gezeigt, dass die folgende Triggerstrategie f¨ur die Bildung der Inflationswartungen des privaten Sektors unter bestimmten Umst¨anden ein e zientes teilspielperfektes Gleichgewicht unterst¨utzen kann:
Triggerstrategie: Setze in Periode 1 die Inflationserwartungen auf π1e = 0. Setze danach f¨ur alle t > 1 die Inflationserwartungen gem¨aß
πt = ( ( |
α |
|
yN |
f¨ur maxi |
πt−i > 0, i ≥ 1 |
(4.43) |
|
e |
|
0 |
|
f¨ur πt−i = 0, i ≥ 1 |
|
||
γ−1)β |
|
|
|
|
|||
|
|
|
|
|
|||
In Worten: Der private Sektor gibt der Zentralbank einmal einen ”Vertrauensvorschuss”, der aber sofort und f¨ur alle Zeiten aufgebraucht ist, wenn dieses Vertrauen einmal missbraucht werden sollte.1
1Daher ist (4.43) eine ”grim strategy”. Die gleiche Analyse l¨asst sich auch hier f¨ur etwas weniger rigorose Bestrafungsstrategien, wie z.B. tit for tat durchf¨uhren. Es andert¨ sich dadurch nichts an der Logik der Analyse, wohl aber an der genauen Bedingung, unter der das e ziente Gleichgewicht des one-shot games die Eigenschaft der Teilspielperfektheit aufweist. Es leuchtet ein, dass Teilspielperfektheit umso eher gegeben ist, je h¨arter die Bestrafungsstrategie ist; der Grund daf¨ur ist der, dass Bestrafung als Abschreckung dient – und diese naturgem¨aß umso eher wirkt, je bedrohlicher sie ist.
