
vysshaya_matematika_1001
.pdf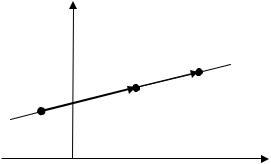
M1M2 x2 x1,y2 y1 (рис. 3.3). Эти векторы коллинеарны (ле-
жат на одной прямой), поэтому их соответствующие координаты пропорциональны:
x x1 |
|
y y1 |
. |
(3.1.6) |
x2 x1 |
|
|||
|
y2 y1 |
|
||
Полученное уравнение называется уравнением прямой, про-
ходящей через две данные точки.
y
M2(x2, y2 )
M(x,y)
M1(x1,y1)
O |
x |
Рис. 3.3. Уравнение прямой на плоскости, проходящей через две данные точки
Заметим, что данное уравнение можно рассматривать также и как каноническое уравнение прямой с начальной точкой M1(x1,y1)
и направляющим вектором прямой s M1M2 x2 x1,y2 y1 .
Уравнение прямой с угловым коэффициентом
Пусть дана начальная точка прямой M0(x0,y0) и ее направ-
ляющий вектор s m,n . Запишем параметрические уравнения прямой (3.1.3) в виде
x x0 mt,
y y0 nt.
Если m 0, то, разделив почленно первое уравнение на второе, получим
81
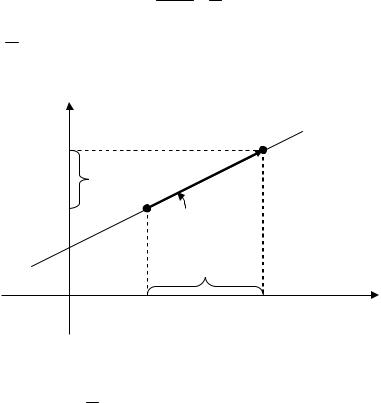
y y0 n . x x0 m
Но n tg , где – угол, образованный прямой с положительным m
направлением оси абсцисс (рис. 3.4).
Число k tg называется угловым коэффициентом прямой.
y |
|
y |
M(x,y) |
sr |
n
y0 

M0 (x0, y0)
m
O |
x0 |
x |
x |
Рис. 3.4. Уравнение прямой с угловым коэффициентом
Заменив n k , из последнего уравнения получим уравнение m
y y0 |
k(x x0), |
(3.1.7) |
которое называется уравнением прямой, проходящей через данную точку с данным угловым коэффициентом или уравнением пучка прямых с угловым коэффициентом.
В последнем случае считается, что угловой коэффициент k принимает все возможные значения k , при этом все пря-
мые пучка проходят через одну и ту же точку M0(x0,y0), называе-
мую центром пучка.
82
Из уравнения (3.1.7) получаем y kx y0 kx0 . Положим
y0 kx0 b, тогда y kx b .
Если x 0 , то y b, где b – величина отрезка, отсекаемого
прямой на оси ординат.
Уравнение прямой
y kx b , |
(3.1.8) |
где k – угловой коэффициент прямой, а b – величина отрезка, отсекаемого прямой на оси ординат, называется уравнением прямой с угловым коэффициентом.
Если же в параметрических уравнениях прямой (3.1.4)
x x0 mt,
y y0 nt
m 0, то направляющий вектор прямой s 0,n и прямая парал-
лельна оси ординат, а ее уравнение, как это следует из первого уравнения (3.1.3), принимает вид x x0 0 или x x0 .
Уравнение прямой в отрезках на осях
Пусть прямая не параллельна ни одной из координаиных осей и не проходит через начало координат. Это значит, что в общем уравнении прямой Ax By C 0 ни один из коэффициентов A, B,
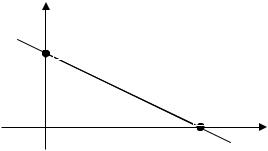
C не равен нулю. Прямая пересекает оси координат в точках
(a,0), (0,b) (рис. 3.5).
y
(0,b)
(a,0)
O |
x |
Рис. 3.5. Уравнение прямой в отрезках на осях
83

Выразим коэффициенты в уравнении прямой через величины отрезков на осях a и b. Подставим в общее уравнение прямой координаты точек (a,0), (0,b) и получим:
A a B 0 C 0 A |
C |
; |
A 0 B b C 0 B |
C |
. |
|
|
||||
|
a |
|
b |
||
Подставляя в общее уравнение прямой вместо A и B их значения, имеем
C x C y C 0. a b
После переноса свободного члена C в правую часть уравне-
ния и деления на C получаем уравнение прямой в отрезках на осях
x |
|
y |
1. |
(3.1.9) |
|
|
ab
3.2.Угол между двумя прямыми на плоскости
Пусть заданы две прямые общими уравнениями
A1x B1y C1 0 и A2x B2 y C2 0,
где N1 A1,B1 , N2 A2,B2 – нормальные векторы прямых. Очевидно, угол между прямыми будет равен углу между их нормаль-
ными векторами, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N ,N ) |
|
|
|
A A B B |
|
|
|||||
cos cos(N , N |
|
) |
1 |
2 |
|
|
|
1 2 |
1 2 |
|
. |
||
|
|
|
|
|
|
|
|||||||
1 |
2 |
|
N |
N |
2 |
|
|
A2 |
B2 |
A2 |
B2 |
||
|
|
|
1 |
|
|
|
1 |
1 |
2 |
2 |
|
||
Условие перпендикулярности прямых совпадает с условием перпедикулярности нормальных векторов этих прямых:
A1A2 B1B2 0,
а условием параллельности прямых является условие параллельно-
сти их нормальных векторов, что выражаетcя пропорциональностью их соответствующих координат:
A1 B1 .
A2 B2
Пусть две прямые заданы теперь параметрическими, или каноническими, уравнениями с направляющими векторами s1 m1,n1
84
и s2 m2,n2 . Очевидно, угол между прямыми будет равен углу между их направляющими векторами, поэтому
|
(s ,s ) |
|
|
|
m m |
nn |
|
. |
||||
cos cos(s |
,s ) |
1 |
2 |
|
|
|
1 2 |
1 2 |
|
|||
|
|
|
|
|
|
|||||||
1 |
2 |
s |
s |
2 |
|
|
m2 |
n2 |
m2 |
n2 |
||
|
|
1 |
|
|
|
1 |
1 |
2 |
2 |
|
||
Условие перпендикулярности прямых совпадает с условием перпедикулярности направляющих векторов этих прямых
m1m2 n1n2 0,
а условием параллельности прямых является условие параллельно-
сти их направляющих векторов, что выражаетcя пропорциональностью их соответствующих координат:
m1 n1 . m2 n2
Пусть теперь прямые заданы уравнениями с угловыми коэффициентами:
|
y k1x b1 |
и y k2x b2 , |
|
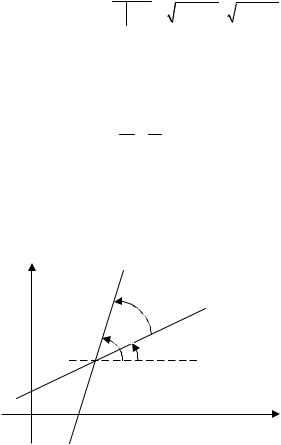
где k1 tg 1, |
k2 tg 2 (рис.3.6). Требуется вычислить |
tg , где |
|
2 1 . |
|
|
|
|
|
y k2x b2 |
|
|
|
|
|
|
2 |
y k1x b1 |
|
|
1 |
|
|
|
|
|
|
O |
x |
Рис. 3.6. Угол между двумя прямыми с угловыми коэффициентами
По формуле из тригонометрии имеем
tg tg( 2 1) |
tg 2 tg 1 |
|
|
k2 k1 . |
||
1 tg tg |
2 |
1 k k |
2 |
|
||
|
1 |
|
1 |
|
||
|
85 |
|
|
|
|
|
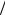
Итак, |
tg |
k2 k1 |
. |
|
|||
|
1 k1k2 |
||
Если прямые параллельны, то tg 0, k2 k1 0, и условие
параллельности прямых выражается равенством их угловых коэффициентов:
k1 k2 .
Если |
прямые |
взаимно |
|
перпендикулярны, |
то |
||||
ctg (1 tg ) 0; 1 k1k2 0, |
и условие перпендикулярности пря- |
||||||||
мых можно представить в виде |
|
|
|
1 |
|
|
|||
|
k k |
|
1 |
или k |
|
|
. |
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
2 |
|
k |
|
|
|
|
|
|
|
|
1 |
|
|
|
3.3. Плоскость в пространстве
Общее уравнение плоскости
Пусть задана декартова прямоугольная система координат в пространстве и линейное уравнение
Ax By Cz D 0 |
(3.3.1) |
в этой системе, причем A2 B2 C2 0, т.е. хотя бы одно из действительных чисел A, B и C не равно нулю.
Покажем, что уравнение (3.3.1) есть уравнение плоскости. Выберем точку M0(x0,y0,z0) , координаты которой удовле-
творяют этому уравнению:
Ax0 By0 Cz0 D 0.
Вычтем из уравнения (3.3.1) почленно полученное равенст-
во:
A(x x0) B(y y0) C(z z0) 0. |
(3.3.2) |
|
Левую часть этого уравнения можно рассматривать как ска- |
||
лярное произведение некоторого |
вектора N A,B,C |
на вектор |
M0M x x0,y y0,z z0 , где |
координаты произвольной точки |
|
M(x,y,z) удовлетворяют уравнению (3.3.1). Тогда |
уравнение |
|
(3.3.2) можно представить в форме |
|
|
(N,M0M) 0. |
|
|
86
Вектор M0M перпендикулярен вектору N , и, значит, все точки M(x,y,z) лежат на плоскости, проходящей через точку M0
(рис. 3.7) перпендикулярно к вектору N .
Обратно, для любой точки M(x,y,z) , лежащей на указанной
плоскости, вектор M0M перпендикулярен вектору N .
Следовательно, уравнение (3.3.1) есть уравнение плоскости. Определение. Уравнение вида
Ax By Cz D 0
называется общим уравнением плоскости.
Вектор N A,B,C , перпендикулярный к плоскости (3.3.1), называется нормальным вектором этой плоскости.
z
N
M
M0
O |
y |
x
Рис. 3.7. Общее уравнение плоскости
Отметим частные случаи положения плоскости относительно системы координат:
1) если в уравнении (3.3.1) свободный член D 0, т.е.
Ax By Cz 0,
то плоскость проходит через начало координат, так как координаты точки O(0;0;0) удовлетворяют уравнению;
87
2) если две из координат нормального вектора N A,B,C равны нулю, то плоскость параллельна одной из координатных плоскостей. Например, для N A,0,0 плоскость Ax D 0 парал-
лельна координатной плоскости yOz;
3) если одна из координат нормального вектора равна нулю, то плоскость параллельна одной из координатных осей. Например,
для N A,B,0 плоскость Ax By D 0 параллельна оси ап-
пликат.
Заметим, что уравнение (3.3.1) можно умножить на любое число, неравное нулю, и полученное уравнение будет уравнением той же самой плоскости.
Уравнение плоскости в отрезках на осях
Пусть плоскость не параллельна ни одной из координатных осей и не проходит через начало координат. Это значит, что в общем уравнении плоскости Ax By Cz D 0 ни один из коэффициен-
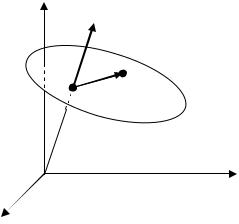
тов A, B, C, D не равен нулю. Плоскость пересекает оси координат в точках (a,0,0), (0,b,0),(0,0,c) (рис. 3.8).
z
(0,0,c)
O |
(0,b,0) y |
(a,0,0)
x
Рис. 3.8. Уравнение плоскости в отрезках на осях
88
Выразим коэффициенты в уравнении плоскости через величины отрезков на осях a,b,c . Подставим в общее уравнение плоскости координаты точек (a,0,0), (0,b,0),(0,0,c) и получим:
A a B 0 C 0 D 0 A D ; a
A 0 B b C 0 D 0 B D ; b
A 0 B 0 C c D 0 C D . c
Подставляя в общее уравнение плоскости вместо A,B,C их значения, имеем
D x D y D z D 0. a b c
После переноса свободного члена D в правую часть уравне-
ния и деления на D получаем уравнение плоскости в отрезках на осях:
x |
|
y |
|
z |
1. |
(3.3.3) |
a |
b |
|
||||
|
|
c |
|
|||
Уравнение плоскости, проходящей через три данные точки
Даны три точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3),
не лежащие на одной прямой (рис. 3.9). Требуется найти уравнение плоскости, проходящей через эти точки.
M2 (x2,y2 ,z2)
M3(x3, y3,z3)
M(x,y,z)
M1(x1 , y1,z1)
Рис. 3.9. Уравнение плоскости, проходящей через три данные точки
89

Пусть M(x,y,z) – произвольная точка плоскости. Чтобы
точка M лежала в плоскости, проходящей через точки M1,M2,M3 ,
необходимо и достаточно, чтобы векторы M1M2, M1M3, M1M бы-
ли компланарны.
Условие компланарности векторов выражается равенством нулю их смешанного произведения
(M1M, M1M2, M1M3) 0.
Если выразить векторы в координатной форме:
M1M x x1,y y1,z z1 , M1M2 x2 x1,y2 y1 ,z2 z1 ,
M1M3 x3 x1,y3 y1 ,z3 z1 ,
то смешанное произведение можно записать в виде определителя, и
уравнение плоскости, проходящей через три данные точки, примет вид
x x1 |
y y1 |
z z1 |
|
|
x2 x1 |
y2 y1 |
z2 z1 |
0. |
(3.3.4) |
x3 x1 |
y3 y1 |
z3 z1 |
|
|
Чтобы привести уравнение (3.3.4) к общему виду, достаточно вычислить коэффициенты A, B, C, D, разлагая определитель по элементам первой строки.
Заметим, что если бы точки M1,M2,M3 лежали на одной
прямой, то вторая и третья строки в определителе уравнения (3.3.4) были бы пропорциональны и все коэффициенты уравнения плоскости были бы нулями.
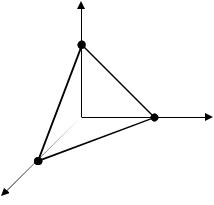
3.4. Угол между двумя плоскостями
Углом между двумя плоскостями называется угол между век-
торами, нормальными к этим плоскостям (рис. 3.10).
Пусть плоскости Пл1 и Пл2 заданы общими уравнениями
A1x B1y C1z D1 0 и A2x B2 y C2z D2 0.
Нормальные векторы к этим плоскостям соответственно равны:
N1 A1,B1,C1 |
и N2 A2,B2,C2 . |
|
90 |
