Эконометрика. Учебное пособие

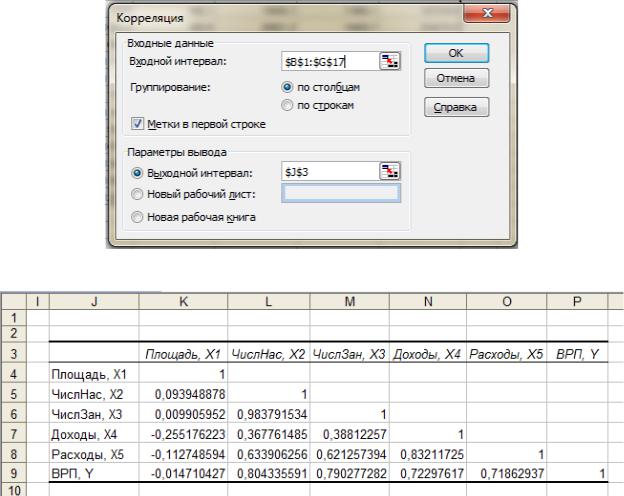
Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Отбор факторов, включаемых в регрессию, является одним и из важнейших этапов практического использования методов регрессии. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов k обычно в 6—7 раз меньше объема совокупности n, по которой строится регрессия.

Пример 12. Для данных из примера 11 получить корреляционную матрицу и выяснить, какие факторные переменные целесообразно включать в уравнение регрессии.

Корреляционную матрицу можно получить с помощью инструмента Корреляция, содержащегося в Анализе данных. Заполнение соответствующего диалогового окна представлено на рисунке 4.5 (исходные данные располагаются так, как показано на рисунке 4.2). Результат содержится на рис 4.6.

Рис. 4.5. Заполнение диалогового окна Корреляция

Рис. 4.6. Результаты корреляционного анализа

Выведенная на экран матрица не содержит элементов выше главной диагонали, поскольку корреляционная матрица симметрична и элементы расположенные выше главной диагонали равны соответствующим элементам, которые расположены ниже.

61

Также отметим, что данная таблица является расширенной корреляционной матрицей, поскольку содержит не только коэффициенты корреляции между факторными переменными, а также и коэффициенты корреляции между факторными переменными и зависимой переменной Y (последняя строка).

Проведем анализ полученной матрицы. Коэффициент корреляции между факторами X3 и X2 равен 0,98>0,7. Следовательно, эти факторы коллинеарны и один из них необходимо удалить из модели. Поскольку коэффициент корреляции между X3 и Y равен 0,79, а коэффициент корреляции между X2 и Y равен 0,8, то из модели необходимо удалить X3 (удаляем ту из переменных, которая имеет меньший коэффициент корреляции с Y). Аналогично, из пары коллинеарных переменных X4 и X5 удаляем X5.

4.5. Коэффициент детерминации

Коэффициент детерминации R2 , также как и для парной регрессии, является характеристикой тесноты связи между y и набором регрессоров x(1) , x(2) ,…, x(k) и определяется по формуле:

где общ (yi y)2 , рег (yi* y)2 и ост (yi yi*)2 .

Как и для случая парной регрессии, множественный коэффициент корре-

ляции изменяется в пределах от 0 до 1. Приближение R2 к единице свидетель-

ствует о сильной зависимости. Если R2 мал по величине, то можно утверждать, что либо не все важные факторы взаимосвязи учтены, либо выбрана неподходящая форма уравнения.

В случае парной регрессионной зависимости было показано, что коэффициент детерминации совпадает с квадратом выборочного коэффициента корре-

ляции. В случае множественной регрессии коэффициент детерминации R2 может быть определен по значениям парных коэффициентов корреляции следующим образом:

где rij – парные коэффициенты корреляции между регрессорами x(i) и x( j) , a

ri0 – парные коэффициенты корреляции между регрессором x(i) и y.

В числители данной формулы находится обобщенный коэффициент корреляции, для всей системы переменных, а в знаменателе обобщенный ко-

эффициент корреляции регрессоров.

Рассмотрим частные случаи данной формулы. В случае парной зависимости формула имеет вид

что совпадает с формулой, полученной нами ранее.

Для случая зависимости результативного признака от двух факторных признаков формула коэффициента множественной корреляции имеет вид:

R2 1 r102 r202 2r102r202 r122 . 1 r122

Коэффициент R2 показывает абсолютный размер влияния регрессоров на зависимую переменную. При увеличении числа объясняющих переменных зна-

чение R2 возрастает, поэтому данный показатель становится ненадежным.

Скорректированный (нормированный) коэффициент детерминации R2

накладывает штраф за увеличение числа независимых переменных. Этот коэффициент определяется следующим образом:

где n – количество наблюдений, k – количество объясняющих переменных. Добавление объясняющей переменной в модель всегда уменьшает ост ,

хотя бы незначительно. Если это уменьшение мало, то оно скорректируется уменьшением знаменателя и R2 не изменится, в отличии от обычного коэффи-

циента детерминации R2 , значение которого будет возрастать в любом случае.

4.6. Проверка значимости линейной регрессионной модели

Проверка значимости линейной регрессионной модели, как и в случае парной регрессии, осуществляется с помощью критерия Фишера. Рассмотрим нулевую гипотезу

H0 : 1 2 ... k 0

при альтернативной гипотезе

H1 : среди коэффициентов 1, 2,..., k

63

хотя бы один отличен от нуля.

Справедливость гипотезы H0 означает, что модель незначима, соответственно, справедливость гипотезы H1 означает значимость модели.

Чтобы проверить H0 по имеющейся выборке объема n, необходимо вы-

числить наблюдаемое значение критерия

пенями свободы k и (n k 1). При помощи функции FРАСПОБР по заданному уровню значимости и степеням свободы k и (n k 1) определяем критическую точку Fкр F ,k,n k 1 FРАСПОБР ,k,n k 1 . Если

Fнабл Fкр с некоторым уровнем значимости (обычно берут 0,05), то

нулевая гипотеза отвергается и регрессия считается значимой. В противном случае нет оснований для того чтобы отвергнуть нулевую гипотезу, поэтому полученное уравнение регрессии считается незначимым.

4.7. Сравнение «короткой» и «длинной» моделей

Помимо проверки уравнения в целом можно также проверить значимость совместного вклада группы регрессоров. Предположим, что сначала оценивается регрессия с k независимыми переменными («короткая» модель):

y 0 1x(1) 2x(2) ... k x(k) .

Остаточную сумму квадратов для этой модели обозначим через корост . Затем добавляются еще q переменных и рассматривается регрессия с k q независимыми переменными («длинная» модель):

y 0 1x(1) 2x(2) ... k x(k) k qx(k q) .

Остаточную сумму квадратов для этой модели обозначим через остдлн .

Разумеется, добавление дополнительных регрессоров x(k),x(k 1), ,x(k q) не ухудшает качество модели в том смысле, что, в силу очевидного соотноше-

ния остдлн корост , коэффициент детерминации «длинной» модели не меньше коэффициента детерминации «короткой модели». Однако, если все коэффициенты k 1, k 2,..., k q равны нулю, то дополнительные регрессоры не оказы-

вают какого-либо влияния на y и их включение в модель не является целесообразным.

64

H1 : среди коэффициентов k 1, k 2,..., k q

хотя бы один отличен от нуля.

Чтобы проверить H0 по имеющейся выборке объема n, необходимо вы-

числить наблюдаемое значение критерия

Если H0 верна, то статистика Fнабл имеет распределение Фишера со сте-

пенями свободы q и (n k q 1). При помощи функции FРАСПОБР по заданному уровню значимости и степеням свободы q и (n k q 1) определяем критическую точку Fкр FРАСПОБР ,q,n k q 1 . Если Fнабл Fкр с некоторым уровнем значимости (обычно берут 0,05), то нулевая гипотеза отвергается, следовательно, все дополнительные регрессоры признаются значимыми. В противном случае делается вывод о том, что дополнительные регрессоры не улучшают качество модели и их введение не целесообразно.

4.8. Оценка значимости коэффициентов регрессии по t-критерию Стьюдента

В случае множественной регрессии, для каждого отдельного фактора используется формула оценки значимости

bj

tнабл, j Sj

где bj – коэффициент чистой регрессии при факторе xj , Sj – стандартное

стандартное квадратичное отклонение оценки коэффициента регрессии может быть определено по следующей формуле:

нации для уравнения множественной регрессии, Sxj – среднее квадратичное от65

клонение для признака xj , Rxjx2 1...xp - коэффициент детерминации для зависимо-

сти фактора xj со всеми другими факторами уравнения множественной регрессии, n – число наблюдений.

Доверительный интервал для коэффициента регрессии j определяется

как

bj t( ,n p 1) Sj .

Отметим, что условие tнабл, j tкр равносильно тому, что доверительный

интервал содержит ноль. Это означает, что если концы доверительного интервала для коэффициента регрессии j имеют разные знаки, то коэффициент j

признается статистически незначимым.

Пример 13. Продолжим анализ данных из примера 11 и построим адекватную регрессионную модель. Прежде всего отметим, что согласно результатам примера 12 из модели нужно удалить переменные X3 и X5. Таким образом, нам необходимо построить регрессию по данным, которые представлены на рисунке 4.7.

Рис. 4.7. Исходные данные без коррелирующих переменных (строки 7-15 скрыты)

Результат применения инструмента Регрессия к этим данным показан на рисунке 4.8.

66

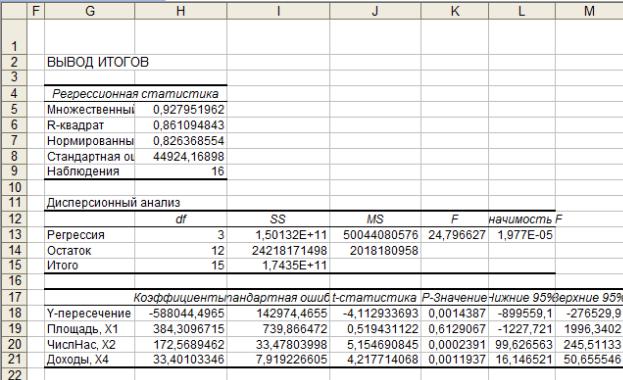
Рис. 4.8. Результаты регрессионного анализа

Кроме коэффициентов регрессии (ячейки H18-H21) данная таблица содержит различные показатели качества. Часть из них мы обсуждали в примере 7. Рассмотрим остальные показатели.

В ячейке K13 содержится наблюдаемое значение критерия Фишера Fнабл для гипотезы H0 : 1 2 ... k 0. Если Fнабл превышает критическое значение

F (k,n k 1), то уравнение множественной регрессии является статистически

значимым при заданном уровне значимости . Уровень значимости традиционно принимают равным 0,05 или 0,01, однако можно взять любое малое положительное чис-

ло. Функция F (k,n k 1) убывает по (чем меньше , тем больше значение

F (k,n k 1)), поэтому модель может быть значима, например, при уровне зна-

чимости 0,01 и не значима при уровне значимости 0,001 (это означает, что вероятность того, что модель «на самом деле» незначима меньше чем 0,01, но больше чем 0,001). Естественно возникает вопрос: при каком наименьшем уровне значимости модель будет значимой? Ответ содержится в ячейке L13. То есть в данном случае модель значима при уровне значимости 1,98 10-5. Столь малое значение говорит об очень высоком уровне надежности построенной модели. Если бы значение ячейки L13 было больше чем 0,05, то это означало бы, что модель не значима и необходимо искать другие факторы, объясняющие y.

В ячейках J18-J21 содержатся tнабл,j, которые позволяют, путем сравнения с критическим значением, проверить значимость каждого коэффициента регрессии в отдельности. Ячейки K18-K21 содержат величины аналогичные Значимости F, содержащейся в ячейке L13. Они показывают минимально возможные уровни значимости, при которых соответствующие коэффициенты регрессии значимы.

67

Ячейки L18-L21 содержат нижние концы, а ячейки M18-M21 – верхние концы доверительных интервалов для соответствующих коэффициентов регрессии (см. пример 7).

Полученная модель имеет достаточно высокие показатели качества (коэффициент детерминации и нормированный коэффициент детерминации). Если убрать из модели одну из факторных переменных, то качество модели, естественно, ухудшится (по крайней мере не улучшится). Однако может оказаться, что это ухудшение будет несущественным. Это означает, что данная переменная не является значимой, то есть не оказывает влияния на Y и, поэтому, ее целесообразно удалить (ради упрощения модели). В нашем случае такой переменной является X1. Это следует из того, соответствующий доверительный интервал (ячейки K19-L19) содержит ноль. Целесообразность удаления X1 также следует из того, что P-Значение для этой переменной равно 0,61, т.е. достаточно велико (вероятность совершить ошибку, считая, что X1 значима, равна 61%). Модель без X1 представлена на рисунке 4.9.

Рис. 4.9. Результаты регрессионного анализа для модели не содержащей X1

Как мы видим, коэффициент детерминации уменьшился незначительно, а нормированный коэффициент детерминации вырос. Это говорит о том, что переменная X1 была лишней. У переменных, которые остались в модели, P-значения достаточно малы (меньше чем 0,05), следовательно, они значимы и окончательное уравнение регрессии будет иметь вид

ПрогнозВРП 554667,84 176,2 ЧислНас 32,1 Доходы .

4.9. Фиктивные переменные

В большинстве случаев в модель регрессии включаются количественные факторные переменные. Однако при проведении некоторых исследований мо-

68

жет возникнуть необходимость во включении в модель регрессии качественных факторных переменных. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, возраст, климатические условия, принадлежность к определенному региону. Для того, чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные необходимо преобразовать в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.

Качественные признаки могут приводить к неоднородности исследуемой совокупности, что может быть учтено при моделировании двумя путями:

•регрессия строится для каждой качественно отличной группы единиц совокупности, т.е. для каждой группы в отдельности, чтобы преодолеть неоднородность единиц общей совокупности;

•общая регрессионная модель строится для совокупности в целом, учитывающей неоднородность данных. В этом случае в регрессионную модель вводятся фиктивные переменные, т.е. строится регрессионная модель с переменной структурой, отражающей неоднородность данных.

Фиктивная переменная – это атрибутивная, или качественная, факторная переменная, которая может принимать только значения 0 и 1.

Модель регрессии, включающая в себя в качестве факторной переменной фиктивную переменную, называется моделью регрессии с переменной структурой.

В качестве примера модели регрессии с переменной структурой можно привести модель зависимости размера заработной платы от стажа работников с различным образованием (среднее, среднее специальное и высшее).

Для включения факторной переменной в модель регрессии нужно использовать две фиктивные переменные, потому что количество фиктивных переменных в модели регрессии должно быть на единицу меньше чем значений качественной переменной.

Общий вид модели размера заработной платы с фиктивными переменны-

ми:

y* a bx cz1 dz2 ,

где x – стаж (количественная факторная переменная), z1 1 для работников с высшим образованием и z1 0 для остальных, z2 1 для работников со сред-

ним специальным и z2 0 для остальных.

4.10. Нарушение предпосылок МНК

В пункте 4.3 были указаны условия применимости метода МНК. Три первых условия касались случайной составляющей . Напомним эти условия:

Математическое ожидание случайного отклонения равно нулю, т.е. M i 0, для любого i;

69

Дисперсия 2 ( i ) не зависит от номера наблюдения i (гомоскедастич-

ность);

cov( i, j ) 0, если i j (отсутствие автокорреляции случайных от-

клонений).

Рассмотрим эти условия более подробно.

Первое условие означает, что нет постоянно действующего фактора, не включенного в модель, но оказывающего влияние на результативный фактор y. Другими словами, случайное слагаемое не должно иметь систематического смещения. Если постоянное слагаемое включено в уравнение регрессии, то можно считать, что это условие выполняется автоматически, так как роль постоянного слагаемого как раз и заключается в том, чтобы учитывать постоянную тенденцию показателя y, не учтенную в уравнении регрессии. Если не выполнено это условие, то оценки параметров уравнения регрессии, поученное с помощью МНК, будут неэффективными и смещенными.

Второе условие означает, что дисперсия случайного слагаемого в каждом наблюдении имеет одно и то же значение. Другими словами, не должно быть априорной причины для того, чтобы в одних наблюдениях величина была больше, чем в других, хотя на практике величина остатков уравнения регрессии

вразных наблюдениях будет разной. Если дисперсии случайного слагаемого зависят от номера наблюдения, то оценки коэффициентов регрессии, полученные с помощью МНК, будут неэффективными и смещенными. Поэтому (по крайней мере, формально) можно получить более надежные оценки с использованием других методов. Например, с помощью обобщенного метода наименьших квадратов (см. [6]).

Третье условие указывает, что между значениями случайного слагаемого

вразных наблюдениях нет систематической связи, т.е. указывает на некоррелированность (на независимость) случайных слагаемых для разных наблюдений. Если это условие нарушается (например, для временных рядов), то имеет место автокорреляция остатков, оценки коэффициентов регрессии, полученные МНК, оказываются неэффективными. Существуют методы диагностирования и устранения автокорреляции.

Поскольку случайная величина недоступна для непосредственного наблюдения, то проверка выполнимости условий 1)-3) осуществляется на основе

анализа остатков ei yi yi* . Здесь, yi – наблюдаемые значения, yi* – значе-

ния, рассчитанные по уравнению регрессии.

Условие 1) для остатков выполняется автоматически, т.к.

ey y* y (a b x) y (y b x b x) 0.

4.11.Проверка гомоскедастичности. Критерий Голдфелда-Квандта

Нарушение гомоскедастичности называется гетероскедастичностью. В

некоторых случаях явление гетероскедастичности можно обнаружить при по-

70