
Методичка (дискретка)
.pdf
e) Побудувати
f
* (x,
y)
. Чи буде функція
f (x, y)
самодвоїстою?
4. Застосовуючи
f (x, y, z) (x y z) x
тотожні перетворення, привести функцію до виду ДНФ, а потім ДДНФ.
5.Функція від трьох змінних набуває значень 1 на наборах № 1, 2, 4, 7. Побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6.З’ясувати, чи будуть повними системи функцій:
|
|
|
|
|
|
||
|
|
a) {x, x1 x2 }; |
b) {x1 | x2}. |
||||
|
7. |
З’ясувати, які з елементарних кон’юнкцій, складених з двох змінних |
|||||
x |
та |
y , |
|
є імплікантами |
функції |
f (x, y) x y . Чи будуть вказані |
|
імпліканти простими? Вказати прості імпліканти. |
|||||||
|
8. |
За допомогою карт Карно мінімізувати булеві функції: |
|||||
|
|
a) |
f x y z x y z x y z x y z x y z ; |
||||
b)
f
x y z t x y z t x y z t x
y z t x
y
z t
.
9. Функція f приймає значення 1 на наборах: 010, 011, 100, 101 та 111.
За допомогою методу Петрика знайти тупикові ДНФ та вибрати серед них мінімальні форми.
10.Привести булеву |
функцію |
f x y z x z x y |
до |
||
мінімізувати її аналітичним методом. |
|
|
|
||
11.За |
допомогою |
методу |
Квайна |
мінімізувати |
|
f (x, y, z) x y z x y z x y z x y z x y z . |
|
|
|||
ДДНФ та
функцію
B6
1. Побудувати таблицю істинності для функції
2. Показати, що |
x |
є фіктивною змінною |
|
формулами: |
|
|
|
a) |
f (x, y, z) ((z y) x) ( y x) z x ; |
||
f (x, y, z)
функції
f
(x y
, що
z
) x .
задана
b)f (x, y, z) ((x y) (x z) (x y z) y .
3.Нехай задана функція f (x, y) (x | y) (x y) x .
a)Який порядковий номер цієї функції?
b)Застосовуючи тотожні перетворення, спростити формулу, яка задає f (x, y) .
c)Розкласти функцію f (x, y)
d)Побудувати ДКНФ функції
за змінною f (x, y) .
x
.
e) Побудувати f * (x, y) . Чи буде функція f (x, y) самодвоїстою?
41

f
4. Знайти диз’юнктивний
(x, y, z) (x y x z) (x y z (z
розклад функції за змінними
x y)) .
x,
z
, якщо
5. Нехай задана функція |
f (x, y, z) (x ( y z)) | ((x y) ~ (x z)) . За |
таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6. Привести до ДДНФ та ДКНФ функцію |
f ((x1 x2 ) x2 ) x2 |
x3 |
шляхом тотожних перетворень та за допомогою таблиць істинності. 7. З’ясувати, чи будуть повними системи функцій:
a) |
{x1 x2 , |
x1
x2
}
;
b)
{x |
|
1 |
|
x |
2 |
} |
|
|
.
8. |
Записати функції, двоїсті до функцій: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) f (x y z) (x y x z) ; |
b) |
f (x y) z t x t . |
|||||||||||||
9. |
З’ясувати, які з елементарних кон’юнкцій, складених з двох змінних, |
|||||||||||||||
є імплікантами функції |
f (x, y, z) x ( y z). Чи будуть вказані імпліканти |
|||||||||||||||
простими?
10.За допомогою карт Карно мінімізувати булеві функції:
a)
f
x
y z x
y z x
y z x
y z x
y
z
;
b) |
f |
x y z t x y z t x y z t x y z t x y z t x
y
z t
.
12.За допомогою методу Петрика знайти тупикові ДНФ та вибрати серед них мінімальні форми для булевої функції, яка задана вектором
значень |
f |
(0,1,1,1,1,1,1, 0) . |
13.Функція
f
приймає значення 1 на наборах: 010, 110, 101 та 111.
Мінімізувати функцію
f
за допомогою методу Квайна.
C6
1. Знайти фіктивні змінні функції
a) |
f |
(0, 0,1,1, 0, 0,1,1) |
; |
f , що задана вектором значень:
b) |
f |
(0, 0,1,1,1,1, 0, 0) . |
2.Скільки існує різних булевих функцій від n нуль (тобто дорівнюють 0 на нульовому наборі)?
3.Спростити формулу (x y) (z y) (x z y
4.Довести тотожності:
a)x y z x | ( y | z) ;
b)x y z (x y z) (x y) ( y z) (
змінних, що зберігають
) .
z x) .
42

5. Нехай задана функція |
f (x, y, z) ((x y z) | (x | y)) ~ (z ( y z)) . За |
таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6. Привести булеву функцію |
f (x, y, z) (x y z) (x z) |
шляхом |
тотожних перетворень до ДДНФ та ДКНФ.
7.Знайти всі самодвоїсті функції від двох змінних.
8.Перевірити рівності:
|
a) x x y |
x y ; |
b) x x y x y . |
|
Записати двоїсті співвідношення та довести їх справедливість. |
||
|
9. Мінімізувати |
за |
допомогою методу Квайна булеву функцію |
f |
x y z t x y z t x y z t x y z t x y z t x y z t . |
||
7. Графи
Приклади розв’язання типових задач |
|
|
|
||||
Задача 1. Нехай |
G (V , E) – зв’язний граф і |
e – деяке його ребро. |
|||||
Позначимо через G |
|
граф, який отримано з G |
вилученням |
ребра |
e . |
||
|
|||||||
Довести, що: |
|
|
|
|
|
|
|
a) граф G |
|
є зв’язним, якщо ребро e належить циклу в графі |
G ; |
|
|||
b) граф G є незв’язним і має рівно дві компоненти зв’язності, якщо ребро e не входить у жодний цикл графа G .
Розв’язання.
a) Нехай дві довільні вершини v і w є зв’язаними у графі G . Покажемо,
|
|
|
|
. Можливі два випадки. Якщо маршрут |
|||||
що вони будуть зв’язаними і у G |
|||||||||
M , |
що |
з’єднує v і w у зв’язному графі |
G , |
не |
містить |
ребро e , то |
|||
вилучення цього ребра не змінить зв’язності |
v |
і w |
у графі |
|
. Якщо ж |
||||
G |
|||||||||
ребро e |
належить маршруту M і e (u1, u2 ) , то маршрут, що веде з v у w |
||||||||
у графі |
|
, можна побудувати таким чином: |
|
|
|
|
|
||
G |
|
|
|
|
|
||||
|
беремо маршрут, що веде з v в u1 ; |
|
|
|
|
|
|||
|
додаємо до нього ту частину циклу, що містив ребро e , яка |
||||||||
|
залишилась у графі G та з’єднуємо вершини u1 і u2 ; |
|
|
||||||
|
беремо маршрут, що веде з u2 в w. |
|
|
|
|
|
|||
|
Отже, побудовано “обхідний” маршрут з v до w. Тому граф G є |
||||||||
зв’язним.
b) Нехай ребро e (u1, u2 ) не належить жодному циклу графа G . Тоді у графі G вершини u1 та u2 будуть незв’язаними і будуть належати двом різним компонентам зв’язності G1 та G2 графа G . Крім того, у графі G
43

стануть незв’язаними ті і тільки ті вершини, які були з’єднані у графі |
G |
маршрутом, що містив ребро |
e . Отже, кожна |
вершина v у G |
|
буде |
|
|
|||||
зв’язаною або з вершиною u1 , або з вершиною u2 |
, тобто v належатиме або |
||||
G1 , або G2 . Це і означає, що G |
|
має рівно дві компоненти зв’язності. |
|
||
|
|
||||
Задача 2. Якщо у простому графі G тільки дві вершини v та w мають непарні степені, то вони зв’язані. Довести.
Розв’язання. Якщо граф G
граф G – незв’язний і вершина
зв’язний, то твердження очевидне. Нехай v належить компоненті зв’язності G1 . За
наслідком з леми про рукостискання кожен простий граф має парну кількість вершин непарної степені. Тому і вершина w повинна належати цій же компоненті, оскільки за умовою інших вершин непарної степені не існує. Отже, вершини v та w зв’язані.
Задача 3. Довести, що графи G1 (V1, E1) та ізоморфні.
1 |
b |
G |
(V |
, E |
) |
2 |
2 |
2 |
|
5  2
2
4 |
|
3 |
a |
d |
|
f |
c |
|
|
|
|
|
|
|
|
||||
G |
G |
2 |
|
|
|||||
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
||
Розв’язання. Побудуємо бієктивне відображення |
h : |
V1 |
|||||||
зберігає суміжність вершин в графах G1 та G2 : |
|
|
|
||||||
h(1) b, |
h(2) f , |
h(3) c, |
|
h(4) a, |
h(5) d . |
|
|||
V2
, що
При побудові відображення враховуємо степінь вершин графів: в графі G1
існує одна вершина степені 4: |
n(1) 4 |
. У графі |
G2 |
теж існує лише одна |
||
|
|
|
|
|
|
|
вершина b степені 4, отже, |
|
|
h(1) b . |
У графі |
G1 |
вершина 1 суміжна з |
вершинами 2 та 5, які мають степінь 2. У графі G2 їм відповідають |
||||||
вершини f та d , отже, можна покласти |
h(2) f |
та |
h(5) d , і т.д. |
|||
Потрібно перевірити, що побудоване відображення дійсно зберігає |
||||||
суміжність вершин. Випишемо множину E1 ребер графа G1 : |
||||||
E1 {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (3, 4), (4, 5)}. |
||||||
Побудуємо множину E |
|
{(h(u), h(v)) | (u,v) E1}: |
||||
|
||||||
E {(b, f ), (b, c), (b, a), (b, d), ( f , c), (c, a), (a, d)}. |
||||||
Очевидно, що E E2 , |
тобто, якщо вершини u та v є суміжними у |
|||||
графі G1 , то їх образи h(u) та h(v) є суміжними у графі G2 . Отже, графи G1 та G2 ізоморфні.
44
Зауважимо, що відображення
Наприклад, |
h(1) b, |
h(2) d, |
h можна побудувати не |
||
h(3) a, |
h(4) c, |
h(5) |
єдиним чином.
f . |
Легко |
перевірити, що це відображення також зберігає суміжність вершин.
Задача 4. Нехай T (V , E) – ациклічний граф, m n 1. Довести, що граф T є деревом.
|V | n, | E | m
і
Розв’язання. Дерево – це зв’язний ациклічний граф. Отже, потрібно довести, що T – це зв’язний граф. Доведення проведемо від супротивного. Нехай T – незв’язний граф, який має k компонент зв’язності: T1, T2 , , Tk ,
причому k 1. |
Тоді кожен |
з |
графів Ti (Vi , Ei ), i 1, , k, |
є деревом. |
||
Нехай |Vi | ni , |
| Ei | mi . |
Тоді |
mi ni 1, i 1, , k . Просумувавши по |
|||
всіх значеннях |
i , маємо: |
|
m1 |
mk n1 |
nk k або |
m n k . |
Врахувавши, що за умовою |
m n 1, маємо |
k 1. Отримали протиріччя |
||||
припущенню k 1. Отже, |
граф |
T має лише одну компоненту зв’язності, |
||||
тобто є зв’язним. Це і означає, що граф Е є деревом.
A7
1. Побудувати діаграму, матрицю суміжності та інцидентності
G (V, E) , |
де |
V {1, 2, 3, 4, 5}, |
E {(1, 2), (2, 4), (1, 5), (3, 2), (3, 5), |
|||||
(5, 4)}. |
|
|
|
|
|
|
|
|
2. Нехай |
задано |
матрицю суміжності |
A |
деякого графа |
G . |
|||
допомогою матриці A визначити: |
|
|
|
|||||
a) |
кількість вершин графа |
G ; |
|
|
|
|||
b) |
кількість ребер графа G ; |
|
G ; |
|
||||
c) |
степінь |
n(v) |
певної вершини v графа |
|
||||
|
|
|
|
|
|
|
|
|
d) |
чи має граф |
G петлі; |
|
|
|
|
||
e) |
чи є G |
повним графом. |
|
|
|
|
||
графа
(4,1),
Як за
3. |
Побудувати діаграму повного графа |
Kn з n |
вершинами для: |
|||
|
а) n 1; |
b) n 2; |
c) n 3; d) |
n 4; |
e) n 5 ; |
f) n 6. |
4. |
Скільки ребер має повний граф з n вершинами? |
|
||||
5. |
Побудувати декілька підграфів графа K5 та декілька його остовних |
|||||
підграфів. |
|
|
|
|
|
|
6. |
Скільки ребер у графі з n вершинами, якщо кожна його вершина має |
|||||
степінь 2? |
|
|
|
|
|
|
7. |
Чи існує граф із n вершинами, усі вершини якого є кінцевими, якщо: |
|||||
|
a) n 10 ; |
b) n 11? |
|
|
|
|
45

8. Побудувати доповнення наведених графів:
|
c |
|
|
a |
||
|
|
|
|
|||
|
|
a |
c |
b |
|
|
|
|
|
|
|||
|
|
|
|
|
||
a) |
|
|
|
|
|
|
b) |
|
|
c) |
|
|
|
a |
b |
d |
|
e |
|
|
|
|
|||||
|
|
|
|
|||
|
|
d |
||||
|
|
|
|
|||
b
e
c
f
9. У певному товаристві з n осіб кожен знайомий з |
k і тільки k |
|||||
іншими особами. Чи можливе таке товариство для: |
|
|||||
a) n 5, k 2; |
b) |
n 5, k 3; |
c) n 2m, k 1; d) |
n 2m, k 3? |
||
10.Нехай графи |
G1 (V , E1 ) і |
G2 (V , E2 ) задано |
за допомогою |
|||
матриць суміжності |
A |
і A |
відповідно, |
V n . Визначити матрицю |
||
|
1 |
2 |
|
|
|
|
суміжності a) G1
A
для графа:
G2 |
; b) |
G1 |
G2
;
c) |
G1 |
\
G2
;
d) |
G1 |
.
11.Чому дорівнює степінь вершини |
v |
у графі |
||
вершинами: |
|
|
|
|
a) n(v) 1 |
; |
b) n(v) m 1; c) |
|
n(v) 0; |
G , якщо у графі d) n(v) k ?
G
з m
12.Нехай задано граф
G
:
3
4
2
1  5
5
Чи буде послідовність вершин 1 2 1 5 2 4 маршрутом? Побудувати:
a)маршрут, який з’єднує вершини 1 та 4 і не є ланцюгом;
b)ланцюг, який з’єднує вершини 1 та 4 і не є простим ланцюгом;
c)прості ланцюги, які з’єднують вершини 1 та 4 і мають найбільшу та найменшу довжини;
d)циклічний маршрут, який містить вершину 1 та не є циклом;
e)цикл, який містить вершину 1 та не є простим циклом;
f)прості цикли, які містять вершину 1 та мають найбільшу та найменшу довжини.
46

13.Нехай задано граф
G
:
|
|
|
7 |
2 |
5 |
6 |
9 |
1 |
|
|
|
|
|
|
|
3 |
4 |
|
8 |
Знайти всі ланцюги, які з’єднують вершини 1 та 9. Скільки серед них буде простих?
14.Довести, що граф G1 ізоморфний графу G2 графу G3 . Показати, що граф G1 ізоморфний графу
та граф
G3 .
G2
ізоморфний
1 |
2 |
3 |
a |
|
b |
v |
|
|
|
|
|
|
|
|
1 |
|
|
|
v |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
6 |
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
4 |
5 |
6 |
e |
|
d |
v |
4 |
|
|
|
v |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
|
G |
|
|
|
|
|
|
|
3 |
|||
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
15.Граф, ізоморфний своєму доповненню, називається самодоповнювальним графом. Довести, що існує тільки один самодоповнювальний граф із чотирма вершинами. Побудувати його.
16.Довести, що кількість вершин
графа дорівнює або |
4k , або 4k 1, |
k |
будь-якого самодоповнювального
N .
17.Довести, що для будь-якого графа доповнення є зв’язним графом.
G (V, E)
він сам або його
18.Побудувати всі дерева з п’ятьма вершинами (з точністю до ізоморфізму).
19.Незв’язний граф, кожна компонента зв’язності якого є дерево, називається лісом. Скільки ребер містить такий граф з n вершинами і k компонентами зв’язності?
20.Довести, що будь-яке дерево з дві кінцеві вершини.
n
вершинами (
n
2
) має принаймні
21.Для графів G1 та G2 побудувати відповідні їм остовні дерева:
a)вилучаючи ребро з кожного циклу;
b)пошуком в ширину;
c)пошуком в глибину.
47

1 |
|
2 |
|
|
3 |
8 |
|
|
|
|
9 |
7 |
|
4 |
|
6 |
5 |
|
|
|
|
|
G |
|
|
1 |
v1
v5
v2
v3
v4 G2
22.Скільки ребер потрібно вилучити зі зв’язного графа |
G (V , E) |
||||||
вершинами та m ребрами, щоб отримати остовне дерево? |
|
||||||
23. Нехай граф G |
задано |
за |
допомогою матриці суміжності |
||||
Побудувати діаграму графа G та його матрицю інцидентності, якщо |
|||||||
|
|
|
|
0 1 11 |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
1 0 1 1 |
|
. |
|
|
|
|
0 0 0 0 |
|
|
|||
|
G |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
з n
AG .
Знайти напівстепені входу і виходу кожної вершини. Зясувати, чи має цей граф джерело та стік.
24. Побудувати орієнтований граф з сімома вершинами, який має 2 недосяжні і 3 тупикові вершини.
B7
1. Побудувати діаграму, матрицю суміжності
G (V, E), де V {1, 2, 3, 4, 5}, E {(1, 5), (2, 3), (2,
та
5),
інцидентності графа
(3, 4), (4,1), (4, 2)}.
2. Нехай граф G1 задано за допомогою матриці суміжності
AG1
, граф
G |
2 |
– за допомогою матриці інцидентності |
BG |
. Побудувати діаграми цих |
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
графів, якщо |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 1 1 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 1 0 |
|
|
|
|
|
1 0 0 1 1 |
|
|
|
|
|
1 0 0 0 |
|
|
|
|
A |
|
1 0 0 0 1 |
; |
B |
|
|
. |
|||
|
|
G1 |
|
|
|
|
|
G2 |
|
|
|
|
|
|
|
|
0 1 0 0 0 |
|
|
|
|
|
0 0 1 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 1 0 0 |
|
|
|
|
|
0 1 0 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
48
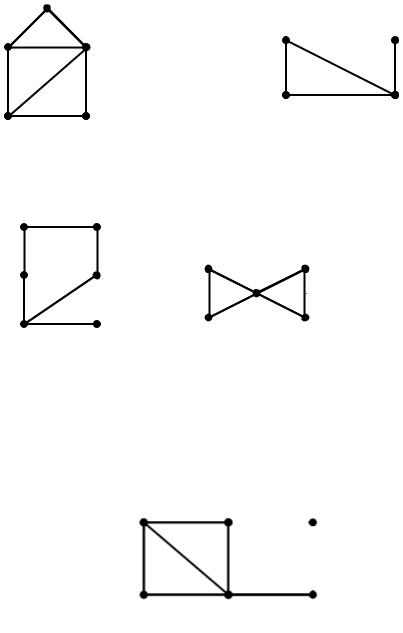
3. |
Побудувати |
всі |
графи |
з |
чотирма вершинами і |
m |
|
(m 0,1, , 6). |
|
|
|
|
|
|
|
4. |
Чи існує повний граф, у якого кількість ребер дорівнює: |
|
|||||
|
a) 15; b) |
18; |
c) 8k |
2 |
2k, |
k N ? |
|
|
|
|
|||||
ребрами
5. Чи існує граф із шістьма вершинами, степені яких дорівнюють: a) 1, 2, 3, 3, 4, 4; b) 2, 3, 3, 4, 4, 4; c) 2, 2, 2, 4, 5, 5.
Відповідь обґрунтувати.
6.Побудувати граф із п’ятьма вершинами, у якому тільки дві вершини мають однакові степені. Чи можуть ці вершини мати степінь 0 або степінь
4?
7.Побудувати об’єднання, перетин, різницю та доповнення графів:
|
e |
|
|
|
|
c |
|
|
|
c |
|
|
d |
|
a |
|
|
a |
|
|
|
||
|
b |
|
|
||
|
|
|
|||
|
|
|
|
||
8. Нехай задано два графи G1 |
та G2 |
: |
|
||
d
b
v |
|
v |
2 |
|
|||
1 |
|
|
v |
|
|
v4 |
a |
c |
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
v |
|
|
v |
d |
|
|
|
5 |
6 |
|
|
|
|
||
|
|
G |
|
G |
2 |
||
|
1 |
|
|
|
|||
Вилучити з графа G1 : |
|
|
|
|
|||
a) |
вершину v5 ; b) |
вершину v3 |
; |
||||
Вилучити з графа G2 |
вершину c . |
|
|||||
9. Нехай задано граф G : |
|
|
|
||||
|
1 |
|
2 |
|
|
||
b e
c) ребро e (v3 , v5 ) .
3
4 |
5 |
6 |
49

a)Вказати степінь кожної вершини.
b)Перевірити лему про рукостискання та її наслідок.
c)Не будуючи доповнення G , вказати, скільки ребер буде мати
граф |
G |
. |
|
|
|
|
d) Чому дорівнюватимуть степені вершин 3 та 5 у графі |
G |
? |
||
|
|
|
|
|
|
10.Нехай у графі G з n вершинами і m ребрами є |
p вершин степеня |
||||
а всі інші вершини мають степінь t 1. Довести, що p (t 1) n 2m.
t
,
11.Кубічний граф – це граф, степінь кожної вершини якого дорівнює 3. Побудувати кубічний граф, що має:
a) 4 вершини; b) 6 вершин; c) 8 вершин. Чи існує кубічний граф з n вершинами, якщо:
а) n 100; |
b) n 101? |
12.Скільки вершин повинен мати кубічний граф? Скільки ребер у |
|
такому графі?
13.Довести, що доповнення кубічного графа не є кубічним графом.
14.Чому дорівнює кількість ребер у графі вершин і k ребер?
G
, якщо
граф
G
має
n
15.Чи існує самодоповнювальний граф, у якого кількість ребер
дорівнює: |
a) 5 |
; |
b) 7 |
? |
16.Побудувати всі самодоповнювальні графи із п’ятьма вершинами.
17.Нехай задано граф
G :
a
d
b |
c |
|
f
Які з наведених нижче послідовностей вершин є маршрутом: a) abcabcd ; b) d f bac f ; c) bcd f ca ; d) d f c ab ?
Вказати ланцюги, прості ланцюги та довжину кожного маршруту. 18.Чи має граф
1
3
2 |
4 |
|
5
50
