Смольянов. тексты лекция

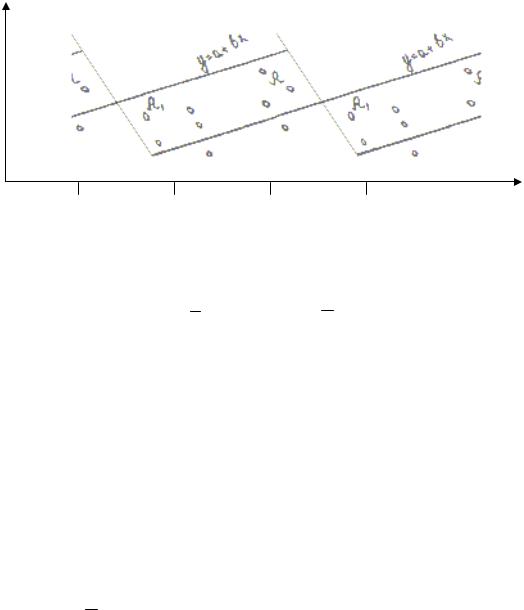
90

x1 y1 = ax1 + bx12 x2 y2 = ax 2 + bx 22

.......... .........

Рис.10.3 Регрессия длины корней на длину стволиков всходов дуба Проведем визуально с целью рассмотрения метода искомую теоретиче-

скую прямую с уравнением: у = а + bx , где y - теоретическая (выравненная) координата. Интересующие нас разности между теоретическими и эксперимен-

тальными ординатами будут – d. При этом di будут иметь и положительные, и отрицательные значения. Вследствие этого в сумме они могут компенсировать

n

друг друга, так что ∑di может оказаться весьма малой или даже равной нулю,

i=1

хотя отдельные отклонения будут большими.

Таким образом, решение поставленной задачи по нахождению теоретической регрессии (в нашем случае линейной) сводится к получению такой линии, для которой сумма квадратов отклонений всех экспериментальных значений у

от вычисленных y является наименьшей (отсюда и название метода). Рассмотрим технику вычисления с использованием способа наименьших

квадратов. Для получения конкретного уравнения в этом случае используется

91

координаты всех точек, которые подставляются в следующую систему уравнений формула (10.1).

Для удобства вычислений числовых значений указанной системы составляется вспомогательная табл. 10.2.

Подставим итоговые данные в систему уравнений и вычислим коэффициенты а, b, имея в виду, что значение «n» соответствует числу классов по х:

Таблица 10.2 Вспомогательные расчеты для вычисления конкретного уравнения

прямой линии

Выравнивание по уравнению параболы. Используя прежний исходный материал (табл. 10.1), проделаем выравнивание опытных данных по уравнению

Получение конкретного уравнения указанного вида сводится, как известно, к определению числовых значений трех коэффициентов (a,b,c). В случае применения способа координат избранных точек, это может быть достигнуто путем использования координат трех точек, подставленных в систему из трех уравнений. Выбор точек и составление системы уравнений выполняется аналогично вышеописанному выравниванию по уравнению прямой линии.

92

В настоящем примере воспользуемся данными классов №1, №3 и №8 из табл.10.1, а именно:

Составим систему из трех уравнений сначала в общем виде:

26,0 = a + 40b + 1600c

В результате решения системы получим следующее конкретное уравнение: (I)

Рассмотрим получение конкретного уравнения способом наименьших квадратов из уравнений общего вида. Система из уравнений общего вида в данном случае будет:

Для получения числовых значений данной системы составляется вспомогательная табл. 10.3.

Проведем визуально с целью рассмотрения метода искомую теоретиче-

скую прямую с уравнением у = а + bx , где y - теоретическая (выравненная) координата. Интересующие нас разности между теоретическими и эксперимен-

тальными ординатами будут называться – d. При этом di будут иметь и положительные и отрицательные значения. Вследствие этого в сумме они могут

n

компенсировать друг друга, так что ∑ d i может оказаться весьма малой или

i =1

даже равной нулю, хотя отдельные отклонения будут большими.

93

Таблица 10.3 Вспомогательные расчеты для вычисления конкретного

уравнения параболы

3 Техника вычисления уровней регрессии. Оценка точности

С целью последующего анализа результатов применения полученных уравнений вычисляются вероятные (теоретические) значения зависимого при-

знака по первому уравнению ( уI ) и второму уравнению ( уII ), которые сравниваются с исходными (опытными) данными ( y ). Указанные ( = y − y ) сравнения производятся по всем классам х, а их результат возводится в квадрат

(2 ) с целью устранения влияния знака. Данные вычисления показаны в табл.

10.4 для прямой линии и табл. 10.5 – для параболы.

Таблица 10.4

Сравнение исходных и вероятных высот деревьев, полученных по уравнению прямой

94

Приведенные в табл. 10.4 и 10.5 данные позволяют, прежде всего, проверить правильность вычислений, выполненных при получении конкретных уравнений, на предмет обнаружения грубых арифметических ошибок.

Правильность вычисления уравнений связи проверяется путем сравнения

исходных значений у с вероятными ( у ), полученными по уравнению I ( уI ) и

уравнению II ( уII ). Критерием правильности вычислений уравнения I будет

совпадение вероятных значений у с исходными значениями у для тех классов, в которых использованы координаты точек в качестве исходных для получения конкретного уравнения I.

Таблица 10.5

Сравнение исходных и вероятных высот деревьев, полученных по уравнению параболы

В нашем примере для уравнения прямой линии значение уI = 18,0 и соответствует исходным данным у в классе №2, т.е. также 18,0. Аналогичное по-

ложение и в следующем классе №6: уI = 23,65. Совпадение у и уI в остальных классах не обязательно и может наступить только случайно.

Некоторый контроль правильности уравнения II можно получить путем сопоставления у и уI во всех классах. В этом случае должно наблюдаться такое сочетание знаков «+» и «–», которое отражает «срединное» положение выравнивающей прямой между выравниваемыми исходными значениями у . О

95

явной неправильности полученного уравнения будет свидетельствовать наличие во всех классах только «+», равно как и знаков «–», или, если в нескольких начальных классах будут наблюдаться отклонения с одним и тем же знаком («+» или «–»), а во всех последующих классах – с противоположным, а именно:

(+++++++); (- - - - - - -); (++++ - - - ) или (- - - - +++). Заметим, что описанные критерии правильности вычислений I и II урав-

нений распространяются и на выравнивание по всем другим линиям связи, в том числе и на уравнение параболы 2-го порядка.

Убедившись в том, что полученные регрессионные уравнения вычислены правильно, можно приступить к оценке точности их «работы», которая может быть выполнена с учетом следующих критериев: мера выравнивания (r1); вели-

чина несовпадения исходных и вероятных значений ( 2 ); среднеквадратиче-

ская ошибка уравнения ( my ); показатель эффективности уравнения ( Fэф ). Приведенные критерии необходимы для выбора оптимального уравнения.

Подробное описание критериев приводится в последующих разделах.

Мера выравнивания. Показатель меры выравнивания ( r1 ) по М.Л. Дворецкому [5] вычисляется по формуле

Из анализа формулы видно, что чем выше абсолютное значение r , тем

точнее «работает» конкретное уравнение регрессии. Если r1 > 0,95, можно считать, что уравнение аппроксимирует опытные данные достаточно точно (надежно).

Для вычисления ri необходимо, прежде всего, получить среднеарифмети-

ческое ( у ) из имеющихся опытных значений у , использовав вышеприведенную формулу:

где N – число наблюдений;

уi - опытные данные отдельных наблюдений;

96

у- среднеарифметическое значение из всех опытных данных.

Затем следует вычислить отклонения (α ) опытных данных от их среднеарифметического:

где у - среднеарифметическое значение из всех опытных данных;

уi - опытные данные.

После этого необходимо определить величину попарных отклонений

() опытных и теоретических значений по формуле

где yi - теоретические данные по уравнению регрессии.

Результаты расчетов отклонений для уравнения прямой линии показаны в табл. 10.6, а для параболы – в табл. 10.7.

Подставим полученные значения в формулу, определим показатель меры

Поскольку в нашем примере r1 = (0,975…0,993) > 0,95, то с вероятностью 0,95 все четыре анализируемых функции аппроксимируют исследуемую взаи-

мосвязь Д Н достаточно надежно.

Величина несовпадения исходных и вероятных значений. Смысл указанного критерия заключается в том, что чем меньше отличаются опытные ( у )

и теоретические ( у ) частоты (или иначе, чем меньше величина ∑ 2 ), тем точнее «работает» уравнение регрессии.

97

Таблица 10.6 Вспомогательные расчеты для получения меры выравнивания ( r1 )

опытных данных по уравнению прямой линии

Вывод: уравнение аппроксимирует опытные данные достаточно точно.

Уравнение II

Вывод: уравнение аппроксимирует опытные данные достаточно точно.

98

Таблица 10.7 Вспомогательные расчеты для получения меры выравнивания ( r1 )

опытных данных по уравнению параболы

Вывод: уравнение аппроксимирует опытные данные достаточно точно.

Из итогов табл. 10.4 видно, что точность выравнивания опытных данных по прямой линии для уравнения I, полученного методом координат избранных

точек, выражается величиной ∑ 2I = 5,3, а для уравнения II, полученного

довало ожидать, трудоемкий и точный способ наименьших квадратов показал более высокую точность выравнивания.

Выравнивание наблюдений по сложной регрессии – параболе второго по-

вательно, обеспечивает увеличение точности выравнивания в сравнении с прямой более чем в три раза. К тому же, как и в уравнении прямой линии, подтверждается более высокая точность работы уравнений, полученных методом

n – число классов (точек), использованных для вычисления уравнения; К - число коэффициентов уравнения.

Величина my показывает размер отклонения фактических значений высот деревьев от вероятных, полученных по уравнениям связи. Уравнение будет «работать» тем точнее, чем меньше абсолютная величина my . Из приведенных

данных видно, что для прямой линии m YII = 0,82 меньше mYI = 0,87. Следовательно, точность «работы» уравнения II, вычисленного методом наименьших квадратов, будет незначительно выше (на 5 %), чем уравнения I, полученного гораздо менее трудоемким путем – методом координат избранных точек. Все это свидетельствует о том, что удачный выбор исходных точек позволяет получить вполне удовлетворительные результаты выравнивания при использовании менее трудоемкого способа – координат избранных точек. С другой стороны, сравнивая результаты «работы» уравнений прямой и параболы, можно увидеть, что в случае использования уравнения параболы ошибка уравнения уменьшается весьма существенно (почти вдвое): 0,49 против 0,82 и 0,53 против 0,87.

Используя результаты вычислений, показанных в табл.10.4, определим ошибку первого, а затем второго уравнения прямой линии: