
МА_технические_семестр1_Пределы Производная Графики Интегралы
.pdf
Ответ: |
|
10x |
7 |
|
. |
|
|
|
|
|
|||
|
|
|
|
|||
2 5x2 |
7x 3 |
|||||
|
|
|
||||
b)y=x5arcsin2x.
Пользуясь правилами дифференцирования (1.35), (1.37) и таблицей производных, получаем:
y |
x5 arcsin 2x x5 arcsin 2x |
5x4 arcsin 2x x5 |
1 2 |
||||||
|
|
||||||||
|
|
||||||||
1 2x 2 |
|||||||||
|
|
|
|
|
|
|
|||
|
5x4 arcsin 2x |
|
2x5 |
|
|
||||
|
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
1 |
4x2 |
|
|
||||
Ответ:
c)
5x4 arcsin 2x |
|
2x5 |
|||||
|
|
|
|
. |
|||
|
|
|
|
||||
|
|
|
1 |
4x2 |
|||
|
x4 |
|
|
|
|
|
|
y |
|
. |
|
|
|
|
|
ln x |
|
|
|
|
|
||
Пользуясь (1.36) и таблицей производных, получаем:
|
x |
4 |
ln x x |
4 |
ln x |
|
4x |
3 |
ln x x |
4 |
1 |
|
x3 (4 ln x 1) |
|
|
y |
|
|
|
x |
|
. |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
ln2 x |
|
|
|
|
|
|
ln2 x |
|
|
|
ln2 x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
x3 (4 ln x |
1) |
. |
|
|
|
|
|
|
|
|
|
|||
ln2 x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d)y=tg23x.
Пользуясь (1.37) и таблицей производных, получаем:
y 2tg3x |
|
|
1 |
|
3. |
|||
|
|
|
|
|||||
cos2 |
|
|||||||
|
|
|
|
3x |
||||
e) |
|
x t5 |
|
2t, y t3 2t 1. |
||||
Пользуясь (1.40) и таблицей производных, получаем: |
||||||||
y |
3t2 |
2 |
. |
|
|
|
||
5t4 |
2 |
|
|
|
||||
|
|
|
|
|
||||
Ответ: |
|
3t2 |
2 |
. |
|
|||
|
5t4 |
2 |
|
|||||
|
|
|
|
|
||||
00.04 |
Вычислить вторую производную функции |
y=x2arctgx. |
Решение. |
|
|
Пользуясь правилами дифференцирования (1.34), (1.35), |
(1.36), (1.41) и |
|
|
51 |
|

таблицей производных, получаем последовательно первую и вторую производные:
y |
x2 |
arctgx |
x2 arctgx |
2xarctgx |
|
x2 |
1 2xarctgx |
1 |
|
, |
|
|
|||
1 |
x2 |
1 x2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
1 |
2 x |
arctgx x arctgx |
1 x2 |
1 |
2 arctgx |
|
x |
|
2x |
. |
||||
|
|
|
|
|
|
||||||||||
|
|
x2 |
|
(1 x2 )2 |
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
Ответ: 2 arctgx |
x3 |
2x |
. |
|
|
||
|
|
|
|
||||
|
1 |
x2 |
2 |
|
|
|
|
|
|
|
|
|
|||
00.04 |
Найти экстремумы функции y |
x2 |
|||||
|
. |
||||||
x 1 |
|||||||
Решение. Рассмотрим функцию при x 1.
Вычислим производную и приравняем ее нулю.
|
2x x 1 x2 |
|
x2 2x |
|
x x 2 |
|
y |
|
|
|
|
|
. |
x 1 2 |
|
x 1 2 |
x 1 2 |
|||
Производная равна нулю при x1=0 и x2=0.
При прохождении критической точки x1=0 производная меняет знак с плюса на минус, значит в ней есть экстремум, а именно – максимум, в
которой функция равна нулю.
При прохождении критической точки x2=2 производная меняет знак с минуса на плюс, значит в ней есть экстремум, а именно – минимум, в
которой функция равна четырем.
Ответ: при x1=0 максимум, y(0)=0; при x2=2 минимум, y(2)=4.
00.05Найти наибольшее и наименьшее значение функции
f(x)=x/2-sinx на отрезке [3π/2;2π].
Решение.
Вычислим производную и приравняем ее нулю.
f (x) |
1 |
cos x. |
|
|
|||
2 |
|||
|
|
Производная равна нулю при cos x |
1 |
, x |
arccos |
1 |
2 n |
|
2 n, n Z. |
|
2 |
2 |
3 |
||||||
|
|
|
|
|
||||
52 |
|
|
|
|
|
|
|

Заданному интервалу принадлежит только критическая точка x=5π/3,
при прохождении которой производная меняет знак с плюса на минус,
значит в ней есть экстремум, а именно – максимум, в которой функция равна
f |
5 |
|
5 |
sin |
5 |
|
5 |
sin 2 |
|
5 |
sin |
|
5 |
|
|
3 |
3, 483. |
|
3 |
6 |
3 |
6 |
3 |
6 |
3 |
6 |
2 |
||||||||||
|
|
|
|
|
||||||||||||||
Вычислим значения функции на концах заданного отрезка
f ( |
3 |
) |
|
3 |
sin |
3 |
|
3 |
1 |
|
3 |
|
1 3,355, |
2 |
4 |
2 |
4 |
4 |
|
||||||||
|
|
|
|
|
|
||||||||
f (2 ) |
|
sin(2 ) |
0 |
|
3,141. |
|
|||||||
Ответ: наибольшее значение функции f |
5 |
|
5 |
|
|
3 |
3, 483, |
|
3 |
6 |
2 |
||||||
|
|
|||||||
наименьшее значение функции f(2π)=π≈3,141.
00.06Провести полное исследование и построить график
функции y |
4x |
|
|
. |
|
4 x2 |
||
Решение.
1)Область определения функции – вся числовая ось.
2)Точек разрыва нет.
3)Функция нечетная (симметрична относительно начала координат).
4)График пересекает ось OX в начале координат.
5)Вертикальных асимптот нет.
Наклонные асимптоты:
k |
lim |
f (x) |
lim |
|
4x |
|
0, b |
lim f (x) kx |
lim |
4x |
|
0. |
|||||
x |
|
2 |
)x |
2 |
) |
||||||||||||
|
x |
|
x |
(4 x |
|
|
x |
|
|
x |
(4 x |
|
|||||
Наклонная (горизонтальная) асимптота y=0. |
|
|
|
||||||||||||||
6) |
|
|
|
4 4 x2 |
|
4x 2x |
|
4 x2 |
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
4 |
|
|
|
. |
|
|
|
|
||
|
|
|
x2 |
2 |
|
|
x2 |
2 |
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|||
Функция возрастает при 0<x<2, убывает при x>2
7)f (x)=0 при x=2. В данной точке максимум f(2)=1.
53
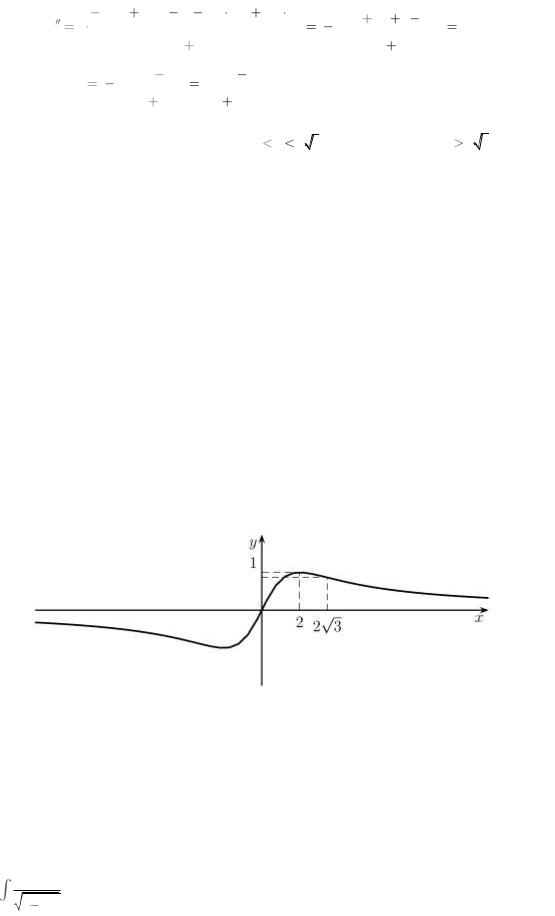
y |
4 |
2x 4 x2 2 |
4 x2 |
2 4 x2 |
2x |
|
|
8x |
|
4 x2 |
8 2x2 |
|
|
|
|
|||||||
|
|
|
4 |
x2 4 |
|
|
|
|
|
|
|
4 |
x2 3 |
|
|
|
||||||
8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x |
12 |
x2 |
|
8x(x2 |
12) |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
|
x2 3 |
4 |
x2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
График функции выпуклый при 0 x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
3; вогнутый при x |
2 3. |
||||||||||||||||||||
Поместим основные данные в таблицу (рис. 3.2). |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
0 |
|
|
(0;2) |
|
|
|
2 |
|
|
|
(2;2 3) |
2 3 |
|
(2 3; ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f(x) |
0 |
|
|
|
+ |
|
|
|
|
1 |
|
+ |
+ |
|
+ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) |
|
|
|
|
|
+ |
|
|
|
|
0 |
|
|
|
|
- |
|
- |
|
- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f (x) |
0 |
|
|
|
- |
|
|
|
|
- |
|
|
|
|
- |
|
0 |
|
+ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
f=0, - |
|
|
f>0, воз- |
|
f=1, |
|
f>0, |
|
|
Пере- |
f>0,убывает, |
||||||||||
Выводы |
перегиб |
|
|
растает, |
|
макси- |
убывает, |
гиб |
вогнута, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
выпукла |
|
мум |
|
выпукла |
|
|
асимптота y=0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис 3.2. График функции
Часть 2 Интегральное исчисление
00.07Вычислить неопределенный интеграл и проверить
результат дифференцированием.
x4dx . 
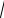 1 x10
1 x10
54
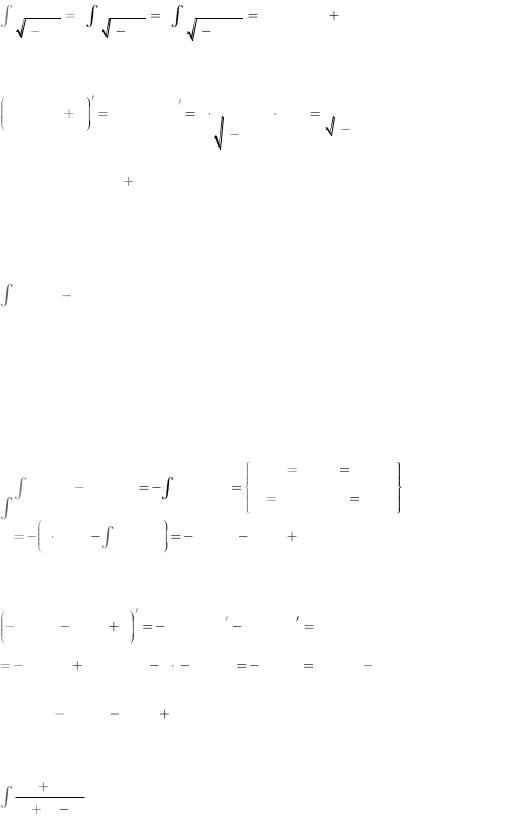
Решение.
Пользуясь простейшими свойствами неопределенного интеграла,
формулой (2.16) и (2.20), получаем:
|
x4dx |
|
|
1 |
|
5x4dx |
|
|
1 |
|
|
d (x5 ) |
|
|
1 |
arcsin x5 |
C. |
|
|
|
5 |
|
|
|
5 |
|
|
|
5 |
||||||||
1 x10 |
|
1 x10 |
|
1 (x5 )2 |
||||||||||||||
|
|
|
|
|||||||||||||||
Проверим полученный результат дифференцированием
|
1 |
arcsin x5 |
C |
|
1 |
arcsin x5 |
1 |
|
1 |
|
|
5x4 |
|
x4 |
|
. |
||
5 |
5 |
5 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 x5 |
2 |
|
|
1 x10 |
|||||||||
Ответ: |
1 |
arcsin |
x5 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00.08 Вычислить неопределенный интеграл и проверить результат дифференцированием.
x sin2 x cos2 x dx.
Решение.
Пользуясь простейшими свойствами неопределенного интеграла и формулой интегрирования по частям в неопределенном интеграле (2.22),
получаем:
|
|
|
|
|
|
|
|
u |
x, du |
|
dx, |
|
x sin2 x cos2 x dx |
x cos 2xdx |
|
dv cos 2xdx, |
v |
|
sin 2x |
||||||
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
x |
sin 2x |
|
sin 2x |
dx |
|
x sin 2x |
|
cos 2x |
C. |
|
|
|
2 |
2 |
2 |
4 |
|
|
|
||||||
|
|
|
|
|
|
|||||||
Проверим полученный результат дифференцированием
|
x sin 2x |
|
|
cos 2x |
|
C |
|
1 |
x sin 2x |
1 |
cos 2x |
|||||
2 |
4 |
|
2 |
4 |
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
1 |
sin 2x x 2 cos 2x |
1 |
|
2sin 2x |
|
x cos 2x x sin2 x cos2 x . |
||||||||
2 |
4 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
|
x sin 2x |
|
cos 2x |
|
|
|
C. |
|
|
||||||
2 |
|
4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
00.09 Вычислить неопределенный интеграл
x 3 dx
x3 x2 2x
.
55

Решение.
Интегрирование правильной рациональной несократимой дроби осуществляется путем разложения на простейшие дроби (см. 2.1.6).
x |
3 |
|
x 3 |
|
A B |
|
C |
|||
|
|
|
|
|
|
|
|
|
|
. |
x3 |
x2 2x |
|
x x 1 x 2 |
x |
x 1 |
x 2 |
||||
A, B, C, найдем методом неопределенных коэффициентов:
|
|
x 3 |
|
|
|
|
|
|
|
A |
|
|
|
|
B |
C |
A x 1 x 2 Bx x 2 Cx x 1 |
, |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x 1 x 2 |
x |
|
|
x 1 x 2 |
|
|
|
|
|
x x 1 x 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
x 3 A x 1 x 2 |
Bx x 2 Cx x 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
x |
0, |
3 |
|
|
2 A, |
|
|
|
A |
|
|
|
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
1, |
4 |
|
3B, |
B |
|
4 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
2, |
|
1 6C, |
|
|
|
C |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя простейшие дроби (2.29), получаем: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x |
3 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
6 |
|
dx |
ln |
|
x |
|
ln |
|
x 1 |
|
ln |
|
x 2 |
|
C. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x3 |
x2 |
|
2x |
|
|
|
|
|
|
x |
|
x 1 |
|
|
|
x 2 |
|
2 |
|
|
|
3 |
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Ответ: |
|
3 |
|
|
|
|
4 |
ln |
|
x 1 |
|
|
|
|
1 |
ln |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
ln |
x |
|
|
|
|
|
|
2 |
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
2 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
00.10Вычислить неопределенный интеграл
dx
3cosx 4sin x .
Решение.
Пользуясь универсальной тригонометрической подстановкой (2.37),
получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
x |
|
t, |
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t2 |
|
|
|
|
|
|
|
2dt |
||||||||||||||
3cosx |
|
4 sin x |
|
|
|
dx |
|
|
|
|
|
|
2dt |
|
, |
|
|
|
3 1 |
t2 |
|
|
|
4 |
2t |
|
3 |
8t 3t2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
t2 |
1 |
|
t2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
d t |
|
4 |
|
|
|
|
|
2 |
|
|
|
1 |
|
t 2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
ln |
|
C |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
|
t |
2 |
|
8 |
|
t |
1 |
|
|
|
|
3 |
|
|
|
|
t |
|
|
4 |
|
2 |
|
25 |
|
3 |
2 |
|
5 |
t |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
ln |
|
|
|
2 |
|
|
|
|
|
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
5 |
|
tg |
|
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
56

|
|
|
tg |
x |
2 |
|
||
1 |
|
|
|
|||||
|
|
2 |
|
|
|
|||
Ответ: |
|
ln |
|
|
|
C. |
||
5 |
tg |
|
x |
|
1 |
|||
|
|
|
2 |
3 |
|
|||
00.11 Вычислить определенный интеграл
ln 8 |
|
dx |
|
|
|
|
. |
||
|
|
|
||
|
|
|
||
ln 3 |
ex 1 |
|||
|
||||
Решение.
Сделаем подстановку в определенном интеграле (2.46) ex+1=t2, exdx=2tdt, eln3+1=4=t2, eln8+1=9.
ln 8 |
dx |
|
ln 8 |
ex dx |
|
3 |
|
2tdt |
3 |
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
t2 1 |
|
|
|
ex |
1 |
ln 3 ex |
ex 1 |
|
|
|
|
1 t |
||||||||||||
ln 3 |
2 |
|
2 |
|||||||||||||||||||
2 |
1 |
ln |
|
t |
1 |
|
3 |
ln |
2 |
|
ln |
1 |
|
ln 3 |
ln 2. |
|
|
|||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
t |
1 |
|
2 |
4 |
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: ln3-ln2.
00.12 Вычислить несобственный интеграл или доказать его
расходимость
xe x2 dx.
0
Решение.
Несобственный интеграл первого рода по определению (2.47) равен:
|
2 |
|
|
|
b |
|
|
2 |
|
|
1 |
|
b |
2 |
|
|
|
|
|
|
|
xe x |
dx |
lim |
xe |
x dx |
lim |
|
|
|
|
e x |
|
2x dx |
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
||||||||||||||
0 |
|
|
b |
|
0 |
|
|
|
b |
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
1 |
b |
|
x2 |
|
|
2 |
lim |
1 |
|
|
|
x2 b |
lim |
1 |
|
b2 |
1 |
|
||
|
|
|
e |
|
d |
x |
|
|
|
e |
0 |
|
e |
1 |
|
. |
|||||
2 |
|
|
|
2 |
|
2 |
2 |
||||||||||||||
b |
0 |
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интеграл сходится и равен ½.
Ответ: ½.
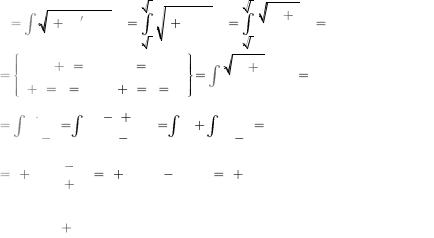
00.13Найти длину дуги кривой y=lnx от x= 3 до x= 8.
Решение.
По формуле (2.54) длина дуги кривой:
57
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
x2 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
))2 dx |
|
|
dx |
||||||||||||||||
L |
|
|
|
1 ( f (x))2 dx |
|
|
|
|
|
|
1 ( |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 |
|
|
|
|
|
t2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
xdx |
|
|
|
tdt, |
|
|
|
|
|
|
|
x2 |
1 |
(xdx) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 1 4 t2 , 8 1 9 t2 , |
|
|
|
|
2 |
|
|
x2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 t |
tdt |
|
|
3 (t2 |
1 |
1)dt |
3 |
|
|
|
|
|
3 dt |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
t2 |
1 |
|
|
|
|
|
|
t2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
1 |
|
|
|
|
|
|
||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
1 |
ln |
|
t |
1 |
|
|
3 |
|
1 |
|
1 |
|
ln |
|
|
2 |
|
|
1 |
ln |
|
|
1 |
|
|
1 |
1 |
ln |
3 |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
t |
1 |
|
2 |
|
|
2 |
|
|
|
4 |
|
|
2 |
|
|
3 |
|
|
2 |
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Ответ: 1 |
|
1 |
ln |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
58

4 Контрольная работа № 2
Вариант № 1
Часть 1. Дифференциальное исчисление
01.01С помощью преобразований на плоскости построить
график функции y |
2x |
1 |
. |
|
|
|
|
x |
3 |
|
|
|
|||
|
|
|
|
|
|
||
01.02 |
Вычислить предел |
lim |
sin 6x |
||||
|
. |
||||||
5arctgx |
|||||||
|
|
|
|
|
x 0 |
|
|
01.03Вычислить производные функций
|
|
|
x3 2x2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
a) |
y |
|
5, |
b) y |
x |
|
3 arcsin 2x, |
|
|
|
|
|
|||||
|
|
e2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
tg 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
c) |
y |
|
|
, d ) |
y |
5x |
x , e) x t ln(cos t), y t ln(sin t). |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
sin 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
01.04 |
|
|
Вычислить вторую производную функции |
y |
|
x |
|
. |
|||||||||
|
|
|
|
|
|||||||||||||
|
|
x2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
01.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x |
6 |
, [ 5;5]. |
x2 |
|
||
|
13 |
||
01.06Провести полное исследование и построить график
функции |
y x 1 2 x 2 . |
Часть 2. Интегральное исчисление
01.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
arctgx 2x 5 |
|
dx |
. |
|
x2 |
|||
|
1 |
|
||
01.08Вычислить неопределенный интеграл и проверить
результат дифференцированием: x2 sin 2xdx.
01.09 |
Вычислить неопределенный интеграл |
|
|
|
2x |
1 |
dx. |
||
|
|
|
|
|
|
||||
|
|
x x2 |
2 |
||||||
|
|
|
|
|
|
||||
01.10 |
Вычислить неопределенный интеграл |
|
|
|
|
|
dx |
||
|
|
|
|
|
. |
||||
8 |
4sin x 7 cos x |
||||||||
|
ln 2 |
|
|
|
|
|
|
|
|
01.11 |
Вычислить определенный интеграл |
ex |
1dx. |
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
|
|

01.12Вычислить несобственный интеграл или доказать его
0
расходимость xex dx.
01.13Вычислить площадь фигуры, ограниченной кривыми
y=ex, y=e-x, x=1.
Вариант № 2
Часть 1. Дифференциальное исчисление
02.01С помощью преобразований на плоскости построить
график функции y |
13 |
3x |
. |
|
|
|
|
|
||
|
x |
5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
02.02 |
Вычислить предел |
lim |
ln 1 |
5x |
. |
|||||
|
|
|
||||||||
e |
4x |
1 |
||||||||
|
|
|
|
|
|
x 0 |
|
|
||
02.03Вычислить производные функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
y |
ln 2sin 3x |
3cos 2x , |
b) |
y |
3x |
4x |
|
5x |
3 , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
c) |
y |
3 tg |
|
, d ) |
y arctg |
e |
4x |
2x, e) |
x |
2t |
sin 2t, y sin3 t. |
|
||||||
x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
02.04 |
|
|
|
|
Вычислить вторую производную функции |
y ln ctg2x. |
||||||||||||
02.05Найти наибольшее и наименьшее значение функции на
заданном промежутке |
y |
x |
cos x, [ |
|
; ] |
|
2 |
2 |
|||||
|
|
|
|
02.06 Провести полное исследование и построить график
функции |
y |
x |
1 2 |
. |
x |
2 |
Часть 2. Интегральное исчисление
02.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
|
arcsin x |
|
dx. |
|
||||
|
|
1 x2 |
||
02.08Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
x |
dx. |
|
|
|||
cos2 x |
|||
|
|
||
60 |
|
|
