
МАТ. АНАЛИЗ, Диф-ое исч-ие ф-ции одной переменной Конспект лекций Часть 2 Николаева
.pdf
|
ТЕОРЕМА (Коши). Пусть функции |
y f (x), y g(x) |
непрерывны |
|||||||||||||||||||||||||||||||
x a,b , дифференцируемы |
|
|
x a,b и |
g x 0, тогда существует точка |
||||||||||||||||||||||||||||||
c a,b |
такая, что |
|
f |
|
b |
|
f |
|
a |
|
|
f |
|
c |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
g b g a |
|
|
c |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ДОКАЗАТЕЛЬСТВО. Покажем, что g b g a . Если бы g b g a , |
|||||||||||||||||||||||||||||||||
то функция |
y g x |
удовлетворяла бы условию теоремы Ролля, |
поэтому су- |
|||||||||||||||||||||||||||||||
ществовала бы точка c1 a,b |
|
|
такая, что g c1 0 – |
противоречие условию. |
||||||||||||||||||||||||||||||
Значит, |
g x 0, |
и |
обе части формулы определены. |
Рассмотрим вспомога- |
||||||||||||||||||||||||||||||
тельную функцию |
F x f x f a |
f b f a |
g x g a . |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g b g a |
|
|
|
|
|
|
|||
|
F x |
непрерывна |
|
x a,b , |
|
|
|
дифференцируема |
x a,b |
и |
||||||||||||||||||||||||
F b F a 0, то есть |
|
|
F x |
|
удовлетворяет условиям теоремы Ролля. Тогда |
|||||||||||||||||||||||||||||
существует точка c a,b , в которой |
|
F c 0, но |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
f b f a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f b f a |
|
|
|
f b f a |
|
f c |
|
|||||||
x f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c g b g a |
|
|
|
|
g c |
, |
|||||||||||||
F |
|
x g b g a g x f |
|
g c g b g a |
||||||||||||||||||||||||||||||
что и требовалось доказать.
Доказанная формула называется формулой Коши.
ПРАВИЛО Лопиталя (теорема Лопиталя-Бернулли). Пусть функции
y f x , y g x |
|
непрерывны |
x (a,b , |
дифференцируемы x a,b , |
|||||||||
g x 0 и lim f |
x limg x 0. Кроме того, существует конечный или бес- |
||||||||||||
x a |
x |
x a |
|
|
|
|
|
|
|
||||
конечный lim |
f |
|
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
x a g x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
f x |
0 |
|
f x |
|
|||
Тогда существует lim |
|
|
|
|
lim |
|
|
. |
|||||
|
|
|
|
||||||||||
|
|
|
|
|
x a g x |
|
0 |
x a g x |
|
||||
ДОКАЗАТЕЛЬСТВО. Так как |
по условию lim f x limg x 0, то |
||
|
x a |
x a |
|
доопределим y f x , y g x в точке x a, полагая |
f a g a 0. Тогда |
||
y f x , y g x станут непрерывными x a,b . Покажем, что |
x a,b |
||
g x 0. Предположим, что g x 0, |
тогда существует |
c1 a,x |
такая, что |
g c1 0, так как функция y g x на a,x удовлетворяет условиям теоремы Ролля. Но по условию g x 0 – противоречие. Поэтому g x 0 x a,b .
51
Функции y f x , y g x удовлетворяют условиям теоремы Коши на любом отрезке a,x , который содержится в a,b . Напишем формулу Коши:
|
f |
|
x |
|
f |
|
a |
|
|
|
f |
|
x |
|
|
|
c |
|
, |
c a,x . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|||||||||
|
g x g a |
|
|
|
|
g x |
|
|
g c |
|
|
|
|
|||||||||||||||
|
|
|
|
f |
x |
|
0 |
|
|
|
|
|
f c |
|
|
|
f c |
|
x a, |
|||||||||
Отсюда имеем: lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
lim |
|
, так как если |
||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||
|
x a g |
|
|
0 |
|
x a g c |
|
|
c a g c |
|
|
|||||||||||||||||
то c a.
Переобозначая переменную в последнем пределе, получим требуемое:
|
|
|
|
|
|
f x |
0 |
|
|
f |
x |
|
|||||||
|
|
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x a g x |
|
0 |
x a g x |
|
|||||||||||
ЗАМЕЧАНИЕ 1. Правило Лопиталя остается справедливым и в том слу- |
|||||||||||||||||||
чае, когда x b и x . |
Оно позволяет раскрывать не только неопределен- |
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ность вида |
|
, но и вида |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f (x) |
|
|
|
f |
|
|
|||||||
|
|
|
|
lim |
lim |
|
|
(x) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
g(x) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x a |
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
ЗАМЕЧАНИЕ 2. Если после применения правила Лопиталя неопределенность не раскрылась, то его следует применить еще раз.
|
ln |
|
x 1 |
|
|
|
|
2 |
x |
0 |
|
|
1 |
|
2 sin xcos |
|
x |
|
||||
ПРИМЕР. lim |
|
|
|
sin |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
0. |
|
ctg x |
|
|
|
|
0 |
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 1 |
|
|
x 1 |
|
x 1 |
|
|
|
x 1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ЗАМЕЧАНИЕ 3. Правило Лопиталя – универсальный способ раскрытия неопределенностей, но существуют пределы, раскрыть которые можно, применив лишь один из изученных ранее частных приемов.
ПРИМЕР. lim |
x2 |
1 |
|
|
|
2x |
|
|
x2 1 |
|
|||||
|
|
|
|
|
lim |
|
|
|
|
|
|
lim |
|
и так |
|
|
|
|
|
|
|
|
x |
||||||||
|
|
|
x2 1 |
||||||||||||
x x |
|
|
|
x 2 |
|
|
x |
|
|||||||
далее.
|
x2 1 |
|
Но, очевидно, lim |
|
1, так как степень числителя равна степени |
|
||
x |
x |
|
знаменателя, и предел равен отношению коэффициентов при старших степенях x.
52

ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА
ТЕОРЕМА 1 (признак монотонности дифференцируемой функции).
Пусть |
|
|
функция |
|
|
y f x |
дифференцируема |
x a,b . Если |
||||
f x 0 x a,b , |
то |
f x не убывает, |
если же |
f x 0 |
x a,b , то f x |
|||||||
не возрастает на a,b . |
|
|
|
|
|
|
|
|
||||
ДОКАЗАТЕЛЬСТВО. |
Пусть |
x1,x2 a,b |
– произвольные точки, тогда |
|||||||||
y f x удовлетворяет условиям теоремы Лагранжа на |
x1,x2 (непрерыв- |
|||||||||||
ность следует из дифференцируемости). Напишем формулу Лагранжа |
||||||||||||
где c x1, |
x2 . |
|
f x2 f x1 f c x2 x1 , |
|
||||||||
|
|
|
|
|
|
|
|
|
||||
Если |
x2 x1 |
и f x 0, x a, b то |
|
|
||||||||
f c 0 |
f x2 f x1 0 |
|
f x2 f x1 |
f x |
не убывает. |
|||||||
Аналогично показывается, что если |
f x 0, то |
y f x |
не возрастает. Тео- |
|||||||||
рема доказана. |
|
|
|
|
|
|
|
|
|
|||
ЗАМЕЧАНИЕ. Из доказательства теоремы следует, |
что если f x 0, |
|||||||||||
то y f x |
|
возрастает, |
а при |
f x 0 |
y f x |
убывает. |
|
|||||
Интервалы, на которых функция либо убывает, либо возрастает, называ- |
||||||||||||
ются интервалами монотонности. |
|
|
|
|
||||||||
ПРИМЕР. Найти интервалы монотонности функции |
|
|||||||||||
|
|
|
|
|
|
|
y x3 3x2 9x 5. |
|
|
|||
|
|
2 |
6x 9 3(x |
2 |
2x 3) 0 x1 3, x2 1. |
|
||||||
y 3x |
|
|
|
|||||||||
Исследуем знак производной (рис. 29). |
|
|
|
|||||||||
|
|
|
|
+ |
|
|
|
– |
|
|
+ |
|
y (x) |
|
|
|
|
|
|
|
|||||
y(x) |
|
|
|
|
-1 |
|
|
3 |
|
х |
||
Рис. 29
Функция убывает на 1;3 и возрастает на ; 1 3; .
53
ТЕОРЕМА 2 (необходимое условие экстремума дифференцируемой функции) Пусть функция y f x имеет в точке x x0 экстремум. Если в этой
точке существует производная, то |
f x0 0. |
|
|
Эта теорема является теоремой Ферма и была доказана ранее. |
|
||
ЗАМЕЧАНИЕ 1. Необходимое условие экстремума достаточным не яв- |
|||
ляется. |
|
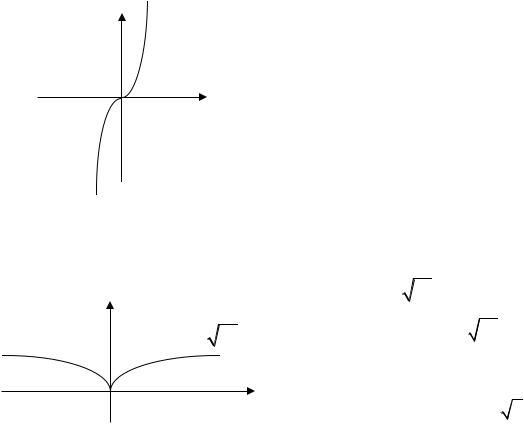
ПРИМЕР. y x3 y 3x2 0 |
x 0, |
|
|
||
у |
y x3 |
но точка x 0 точкой экстремума не яв- |
|
|
|
ляется (рис. 30). |
|
Оx
Рис. 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАМЕЧАНИЕ 2. |
|
Рассмотрим |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
функцию y 3 |
x2 (рис. 31). |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Так как x2 0, |
то y 3 |
|
x2 0, поэтому |
|||||||
y 3 x2 |
|
||||||||||||
|
|
|
x0 0 – точка минимума. Функция не- |
||||||||||
0 |
|
x |
прерывна x R, и y |
|
2 |
|
|
|
y 0 |
||||
|
|
|
|
|
|||||||||
|
|
|
|
33 |
|
x |
|||||||
не существует.
Рис. 31 Таким образом, непрерывная функция может иметь экстремум не только
|
|
|
|
в тех точках, где f (x) 0, но и в тех, где f (x) не существует. |
|
||
ОПРЕДЕЛЕНИЕ. Критическими точками функции y f x называют- |
|||
ся точки, в которых f x 0 или f x |
не существует; при этом точки, в кото- |
||
рых f x 0, называются стационарными точками. |
|
|
|
Не всякая критическая точка является точкой экстремума. |
|
||
ТЕОРЕМА 3 (первое достаточное условие экстремума непрерывной |
|||
функции). Пусть непрерывная функция |
y f x дифференцируема всюду на |
||
a,b за исключением, быть может, критической точки |
x x0 . Если |
f x 0 |
|
54
при x x0 и |
f x 0 |
при x x0 , |
то x x0 – точка минимума; если же |
f x 0 при |
x x0 и f |
x 0 при |
x x0 , то x x0 – точка максимума. |
То есть, если при переходе через критическую точку производная меняет знак с «-» на «+», то в критической точке функция имеет минимум; если с «+» на «-» - то максимум; если же при переходе через критическую точку производная не меняет знак, то экстремума в точке x x0 нет.
|
ДОКАЗАТЕЛЬСТВО. |
Если |
при |
x x0 |
f x 0, |
то по теореме 1 |
|||||
y f x убывает. |
Если |
|
при |
x x0 |
f x 0, то |
y f x возрастает. |
Значит, |
||||
x x0 |
– точка минимума, так как f x0 f x |
x x ;x , 0. |
|
||||||||
|
Если при x x0 |
f x 0, а при |
x x0 |
|
f x 0, то |
y f x |
слева от |
||||
x x0 |
возрастает, а справа – убывает по |
теореме 1. Значит, |
x x0 – точка мак- |
||||||||
симума по определению. |
|
f x 0 (или |
f x 0) при x x0 и при x x0 , то |
||||||||
|
Если окажется, что |
||||||||||
слева и справа от |
x x0 |
y f x |
возрастает (убывает), следовательно, x x0 |
||||||||
точкой экстремума не является. Что и требовалось доказать. |
|
|
|||||||||
|
ПРИМЕР. Найти экстремумы функции |
y x4 4x3 20. |
|
||||||||
y 4x2 12x 4x2 x 3 0 x1,2 0, x3 3.
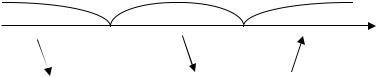
Исследуем знак производной (рис. 32).
|
– |
|
– |
+ |
y (x) |
|
|||
y(x) |
|
0 |
3 |
х |
|
|
|
Рис. 32 |
|
|
В критической |
точке |
x 0 |
экстремума |
нет, |
в критической точке |
x 3 – минимум и ymin |
y 3 7. |
|
|
|
|
Пусть график функции |
y f x имеет касательные во всех точках ин- |
||||
тервала a,b . |
|
|
|
|
|
ОПРЕДЕЛЕНИЕ. График |
функции y f x |
называется выпуклым |
|||
вверх (вниз) на a,b , |
если во всех точках a,b |
он лежит не выше (не ниже) |
|||
любой своей касательной. |
|
|
|
|
|
55
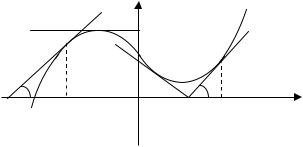
y |
На a,O график |
y f x |
выпуклый вверх, на O,b – вы- |
||
y f (x) |
пуклый вниз (рис. 33). |
|
a |
О |
b |
x |
Рис. 33
ОПРЕДЕЛЕНИЕ. Точкой перегиба графика функции y f x называет-
ся точка M , отделяющая участок графика, выпуклый вверх, от участка, выпуклого вниз.
В этой точке график, можно сказать «перегибается» через касательную.
ТЕОРЕМА 4. (достаточное условие выпуклости вверх (вниз) графика функции). Пусть функция y f x имеет непрерывную вторую производную
x a,b . Тогда, если f x 0, то ее график имеет выпуклость, направлен-
ную вверх, если f x 0, то график функции имеет на a,b выпуклость, на-
правленную вниз.
ДОКАЗАТЕЛЬСТВО. Из определения производной следует, что f x tg – угловой коэффициент касательной к графику в точке x. Заметим
(рис. 34), что на участке графика, выпуклом вверх, касательная поворачивается по часовой стрелке, то есть угол меняется от острого к тупому, поэтому tg f x убывает. На участке графика, выпуклом вниз, касательная повора-
чивается против часовой стрелки, то есть меняется от тупого к острому и
tg f x |
возрастает. |
|
|
|
|
Пусть |
|
0 |
f x |
убывает по теореме 1, значит, |
|
f x 0 f x |
|
||||
tg убывает, и график имеет выпуклость, направленную вверх. |
|||||
Пусть |
|
0 |
f x |
возрастает по теореме 1, и график |
|
f x 0 f x |
|||||
имеет выпуклость, направленную вниз. Что и требовалось доказать.
ТЕОРЕМА 5 (необходимое условие точки перегиба). Пусть функция y f x имеет непрерывную вторую производную в некоторой окрестности точки перегиба x x0 . Тогда f x0 0.
56
ДОКАЗАТЕЛЬСТВО. Пусть f x0 0. Допустим, f x0 0. Так как f x по условию непрерывна, то по теореме об устойчивости знака непре-
рывной в точке функции существует окрестность точки x x0 , в пределах которой f x 0, то есть f x 0 и справа, и слева от точки x x0 . Таким обра-
зом, по теореме 4 y f x имеет выпуклость, направленную вниз, и справа, и
слева от этой точки. Тогда x x0 по определению точкой перегиба не является.
Также приводится к противоречию предположение о том, что f x0 0. Так как по условию f x0 существует, то, следовательно, f x0 0, что и требо-
валось доказать.
ТЕОРЕМА 6 (первое достаточное условие перегиба). Пусть функция y f x имеет непрерывную вторую производную в некоторой окрестности
точки x x0 и |
f x0 0. Тогда, |
если |
при переходе через x x0 |
f x |
меняет |
знак, то x x0 |
– точка перегиба; |
если |
f x не меняет знак, то |
x x0 |
точкой |
перегиба не является. |
|
|
|
|
|
ДОКАЗАТЕЛЬСТВО. Доказать самостоятельно, использую теорему 4.
ПРИМЕР. Построить график функции y x4 4x3 20.
Ранее были найдены интервалы монотонности этой функции и ymin y 3 7.
|
3 |
12x |
2 |
|
12x |
2 |
24x 12x x 2 |
0 |
x1 0, x2 2 – точки переги- |
|
y (x) 4x |
|
|
|
|
||||||
ба (рис. 34), |
|
y 0 20, y 2 4. |
|
|
||||||
|
|
|
|
– |
|
|
– |
|
+ |
|
y (x) |
|
|
|
|
||||||
y(x) |
|
|
|
|
|
|
0 |
3 |
х |
|
|
|
– |
+ |
y (x) + |
|
||
y(x) |
0 |
2 |
х |
|
|
Рис. 34 |
|
57
Строим график с учетом информации о знаках y (x) y
20
5 |
|
|
|
|
|
|
|
|
|
|
|
О |
1 |
|
|
|
|
|
|
|
|||
2 |
3 |
||||
|
|
|
|
|
|
-5 |
|
|
|
|
|
Рис. 35
и y (x) (рис. 35):
x
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
ОПРЕДЕЛЕНИЕ. Прямая линия называется асимптотой кривой, если расстояние от точки M , лежащей на этой кривой, до прямой стремится к нулю при удалении точки M вдоль одной из ветвей кривой в бесконечность.
|
|
|
Асимптоты бывают трех видов: гори- |
|
н |
y в |
|
зонтальные, вертикальные, наклонные |
|
|
y f (x) |
|
(рис. 36). |
|
г |
|
|
г |
– горизонтальная асимптота |
|
|
|
||
|
О |
х |
в |
– вертикальная асимптота |
|
Рис. 36 |
|
н |
– наклонная асимптота |
|
|
|
|
|
ОПРЕДЕЛЕНИЕ. Прямая x a является вертикальной асимптотой кривой y f x , если хотя бы один из односторонних пределов в точке x a бес-
конечен.
В этом случае в точке x a функция имеет разрыв второго рода.
ПРИМЕР. Функция y tg x |
определена при всех x |
|
n, причем |
|
|||
|
2 |
|
|
lim tg x , поэтому график этой функции имеет бесконечное множество
x n
2
вертикальных асимптот.
1
График функции y x 1 x 2 x 3 имеет, очевидно, три вертикаль-
ные асимптоты: x 1, |
x 2, |
x 3. |
58
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ПРИМЕР. |
Функция y 2 |
x 1 |
|
определена |
при |
всех |
x 1, причем |
|||||||
|
1 |
|
1 |
|
|
определению прямая x 1 – вертикальная |
|||||||||
lim 2 |
x 1 |
, lim |
2 |
x 1 |
0. |
По |
|||||||||
x 1 |
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
асимптота графика (справа). |
|
|
|
|
|
|
|
|
|
|
|||||
|
ОПРЕДЕЛЕНИЕ. Прямая |
y kx b называется наклонной асимптотой |
|||||||||||||
графика функции |
y f x |
при |
x (x ), если |
f x |
представима в |
||||||||||
виде: |
f x kx b x , |
lim x 0 |
lim x 0 |
|
. |
|
|
||||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
||
ТЕОРЕМА. Для того, чтобы прямая y kx b была наклонной асимпто-
той графика функции y f x при x (x ), необходимо и достаточ-
но, чтобы существовали два конечных предела:
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|||
lim |
|
|
k, |
lim f x kx b lim |
|
|
|
k, |
lim f |
x kx |
b . |
|||||||||||
|
|
|
x |
|||||||||||||||||||
x x |
|
x |
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
||||||
ДОКАЗАТЕЛЬСТВО. Пусть |
функция |
y f x определена |
при всех |
|||||||||||||||||||
достаточно больших положительных значениях x. |
|
|
|
|
||||||||||||||||||
1. Необходимость: |
y kx b |
|
– асимптота при |
x |
существуют |
|||||||||||||||||
конечные пределы |
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
lim |
|
k, lim f x kx b. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
x |
|
|
|
x |
|
|
|
|
|
|
|
|||
По определению |
f x kx b x , |
lim x 0. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
|
|
f |
x |
|
|
|
|
b |
|
x |
lim f (x) kx lim b x b. |
|||||||||||
Поэтому lim |
|
|
lim k |
|
|
|
|
|
|
|
k, |
|||||||||||
|
x |
x |
|
x |
|
|||||||||||||||||
x |
|
|
x |
|
|
|
|
|
x |
|
|
x |
|
|||||||||
2. Достаточность: существуют конечные |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
lim |
|
f x |
k, |
lim f x kx b y kx b |
|
||||||||||||||
|
|
|
|
x |
|
|||||||||||||||||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
– асимптота при x .
По условию |
lim f x kx b. |
|
x |
Обозначим |
f x kx b x . |
59

Тогда lim x 0, то есть |
f x kx b x , |
где x – б.м. при |
x |
|
|
x . По определению y kx b – асимптота , что и требовалось доказать.
Если x , доказательство аналогично.
ЗАМЕЧАНИЕ. Если при отыскании наклонной асимптоты графика оказалось, что k 0, то график имеет горизонтальную асимптоту y b (если b существует). Если хотя бы один из пределов бесконечен или не существует, то график не имеет ни наклонной, ни горизонтальной асимптот.
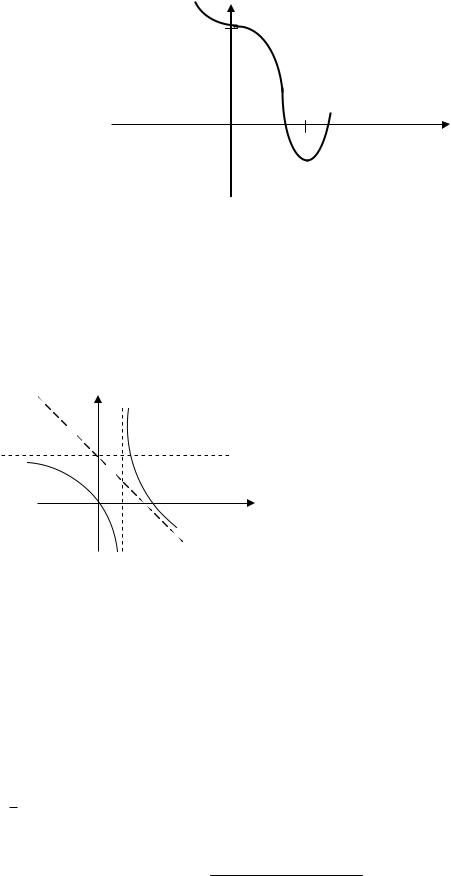
ПРИМЕР. Найти асимптоты графика функции y x 2arctg x. Функция определена x R, значит, вертикальных асимптот нет. Найдем наклонные асимптоты.
k |
|
|
f x |
|
2arctgx |
b |
lim f x kx lim x 2arctgx x . |
|||||
lim |
|
|
|
lim 1 |
|
|
1, |
|||||
|
x |
|
x |
|||||||||
|
x |
x |
|
|
|
x |
x |
|||||
|
Таким образом, при x |
y x – наклонная асимптота. |
||||||||||
k |
|
|
f x |
|
|
2arctgx |
b |
lim f x kx lim x 2arctgx x , |
||||
lim |
|
|
lim 1 |
|
|
1, |
||||||
x |
x |
|
||||||||||
|
x |
x |
|
|
|
|
x |
x |
||||
откуда y x – асимптота графика при |
x . |
|||||||||||
Исследуем первую производную этой функции и построим эскиз графика (рис. 37).
|
|
y |
|
|
2 |
|
x2 |
1 |
|
x1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
1 x2 |
x2 |
1 |
0 |
1. |
|
|||||
|
|
|
|
||||||||||
|
+ |
– |
+ |
|
|
|
|
|
|
|
y x |
|
|
y (x) |
|
|
|
|
|
|
у |
|
|
||||
y(x) |
-1 |
1 |
|
х |
|
|
|
|
|
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
О |
|
х |
Рис. 37
60
