
Boyarshinov_ChM_T3
.pdf
Использование иерархических многочленов
Для построения решения задачи (3.0) – (3.1) на конечном элементе xi, xj
вводятся локальные координаты , с помощью которых строятся иерархические многочлены
|
0 |
1 2 |
, |
|
1 2 |
, |
|
2 |
(1 )(1 ) |
2 |
), |
|
|
|
1 2 |
(1 |
2 |
), … |
|
|
1 |
|
|
|
, (1 |
|
4 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Первоначально решение строится в виде
Tm T0 0 T1 1 T2 2 .
Невязка уравнения теплопроводности (3.0), получаемая на этом решении,
взвешивается по области xi , xj поочередно с каждой из функций 0, 1 и 2,
|
1 |
d 0 d 0 |
1 |
d 0 d 1 |
1 |
d 0 d 2 |
1 |
|
qi |
T0 |
d d d T1 |
d d d T2 |
d d d W 0d 0, |
||||
|
1 |
|
1 |
|
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
T0 d 1 d 0d T1 d 1 d 1d T2 d 1 d 2d W 1d 0, |
||||||||
qj |
||||||||
|
1 d d |
1 |
d d |
1 |
d d |
1 |
||
|
1 |
1 |
1 |
1 |
||||
T0 d 2 d 0 d T1 d 2 d 1d T2 d 2 d 2 d W 2d 0. |
||||||||
|
||||||||
|
1 d d |
1 d d |
1 d d |
1 |
||||
Учитывая, что |
|
|
|
|
|
d 0 |
d 1 2, |
d 1 |
d 1 2, |
d 2 |
d 2 , |
подсчитываются значения интегралов, входящих в эту систему уравнений,
1 d |
0 |
|
d |
0 |
|
1 |
|
1 d |
0 |
d |
|
1 |
|
1 d |
0 |
d |
2 |
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
2, |
|
|
|
|
|
|
|
|
|
0d 1, |
|||||||
d d d 2 |
, |
d d d |
|
d d d 0, |
||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 d d |
0 |
|
1 |
|
1 d d |
1 |
|
1 d d |
2 |
|
|
1 |
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
2, |
|
|
|
1 |
|
|
|
|
1d 1, |
|||||||
d d d 2, |
|
d d d |
|
d d d 0, |
||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 d |
2 |
d |
0 |
|
|
1 d |
2 |
d |
|
|
1 d |
2 |
d |
2 |
|
|
8 |
|
1 |
4 |
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2d |
3 . |
|||||
d d d 0, |
d d d 0, |
d d d 3 |
, |
|||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
Подстановка полученных коэффициентов приводит к системе уравнений
q |
i |
T |
T |
T 0 W 0, |
|||||
|
0 |
2 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
T0 |
|
T1 |
|
T2 |
0 W 0, |
||
qj |
2 |
2 |
|||||||
|
|
|
|
8 |
|
4 |
|||
|
|
|
|
|
|
W |
|||
|
|
T00 T10 T2 |
3 |
0. |
|||||
|
|
|
|
|
|
|
|
3 |
|
61

|
В матричной форме эта система уравнений имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
0 |
|
T |
|
q |
i |
W |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
(3.15) |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
T1 |
qj W |
|
. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
8 3 T |
|
4W 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Теперь рассмотрим вариант аппроксимации решения в виде |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Tm T0 0 T1 1 T2 2 T3 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Взвешенные по области xi , xj невязки уравнения теплопроводности (3.0) |
|||||||||||||||||||||||||||||||||||||||||
приводят к системе уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
T |
1 |
d 0 d 0d T |
1 |
d 0 d 1d T |
1 |
d 0 d 2 d T |
1 |
d 0 d 3d q W |
1 |
|
d , |
|||||||||||||||||||||||||||||||
|
0 |
|
d d |
|
1 |
|
|
d d |
|
2 |
|
|
|
d |
d |
|
3 |
|
|
|
d d |
|
i |
|
|
|
0 |
|
||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
||||||||||||||||||||
|
|
1 |
d 1 |
d 0 |
|
|
|
1 |
d 1 d 1 |
|
|
|
1 d 1 |
d 2 |
|
|
|
|
1 d 1 d 3 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
|
T |
d T |
d T |
d T |
d q |
W |
d , |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
d d |
|
1 |
|
d d |
|
2 |
|
d |
|
d |
|
|
|
3 |
|
d d |
|
|
j |
|
|
1 |
|
|
|
||||||||||||||||
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
1 |
d |
|
d |
|
|
|
|
1 |
d |
|
d |
|
|
|
|
1 |
d |
|
d |
|
|
|
|
|
1 |
d |
|
d |
|
|
|
1 |
|
|
|
|
|
|||
|
T |
2 |
0 d T |
2 |
|
|
|
|
2 |
2d T |
2 |
3d W |
|
|
d , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
1d T |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
0 |
d d |
|
1 |
|
d d |
|
2 |
|
|
d d |
|
3 |
|
|
d d |
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
d |
3 |
d |
0 |
|
|
|
1 |
d |
|
d |
|
|
|
|
1 d |
3 |
d |
2 |
|
|
|
|
1 |
d |
3 |
d |
3 |
|
|
1 |
|
|
|
|
|
||||
|
T |
|
|
|
d T |
|
3 |
1 |
d T |
|
|
|
d T |
|
|
|
d W |
|
|
d . |
||||||||||||||||||||||
0 |
d d |
|
1 |
|
d d |
|
2 |
|
|
d |
d |
|
3 |
|
|
d d |
|
|
|
3 |
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
Поскольку |
d |
d 1 3 2 2, |
|
можно определить значения интегралов, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которые дополнительно входят во вновь сформированную систему уравнений,
1 |
d |
|
d |
|
1 |
d |
|
d |
0d 0, |
|
1 d d |
|
|
|
|
|
1 |
d |
|
d |
, |
|||||||
|
|
0 |
|
3d |
|
3 |
|
|
|
1 |
|
3d |
|
3 |
1d 0 |
|||||||||||||
1 |
d d |
1 |
d d |
|
|
|
1 |
d d |
|
|
|
1 |
d d |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
d |
|
d |
|
1 d |
|
d |
2 d 0, |
|
|
1 |
d |
|
d |
|
|
|
|
2 |
|
1 |
|
||||||
|
|
2 |
|
3d |
|
3 |
|
|
|
|
|
|
3 |
|
3d |
|
, |
|
3d 0. |
|||||||||
1 |
d d |
1 |
d d |
|
|
|
|
1 |
|
d d |
|
|
|
5 |
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подстановка коэффициенты приводит к системе уравнений |
|
|||||||||||||||||||||||||||
|
|
|
|
|
T |
T |
T 0 T 0 q |
i |
|
W, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
2 |
|
1 |
2 |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
T |
T |
T 0 T 0 q |
|
W, |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
0 2 |
|
1 2 |
2 |
|
|
|
3 |
|
|
|
|
j |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
4W |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
T30 |
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
T00 T10 T2 3 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
T 0 T 0 T 0 T |
|
2 |
0, |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
0 |
|
|
1 |
2 |
|
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
которая в матричном представлении имеет вид
62

2 |
2 |
0 |
|
|
2 |
2 |
0 |
|
|||
|
0 |
0 |
8 3 |
|
0 |
0 |
0 |
|
|||
0 |
T0 |
qi |
W |
|
|||
0 |
|
|
|
|
|
|
|
|
T1 |
|
qj |
W |
(3.16) |
||
0 |
|
|
|
|
. |
||
|
T2 |
4W |
3 |
|
|||
2λ 5 |
|
|
|
|
0 |
|
|
|
T3 |
|
|
|
|
||
И, наконец, рассмотрим аппроксимацию решения задачи (3.0) в виде
Tm T0 0 T1 1 T2 2 T3 3 T4 4 .
Выполнение преобразований, аналогичных показанных выше, приводит в конечном итоге к системе линейных алгебраических уравнений
2 |
2 |
0 |
0 |
0 |
T0 |
qi W |
|
|
||||||
|
2 |
2 |
0 |
0 |
0 |
T |
|
|
q |
j |
W |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
0 |
8 3 |
0 |
0 |
|
|
|
|
4W 3 |
|
(3.17) |
||
T2 |
|
. |
||||||||||||
|
0 |
0 |
0 |
2 5 |
0 |
T |
|
|
|
|
0 |
|
|
|
|
0 |
0 |
0 |
0 |
22 λ 105 |
|
3 |
|
|
|
|
|
|
|
|
T |
|
2W 15 |
|
||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
Необходимо отметить, что при аппроксимации решения задачи (3.0) – (3.1) с помощью кусочно-линейного (3.3) и кусочно-квадратичного (3.12) приближений соответствующие системы уравнений (3.8) и (3.14) совершенно различны.
Системы уравнений (3.15), (3.16) и (3.17), полученные при аппроксимации решения той же задачи с помощью иерархической системы функций с 3, 4 и 5 слагаемыми, соответственно, отличаются лишь дополнительными строками и столбцами (выделены жирным шрифтом). Иными словами, при использовании иерархической системы функций для повышении порядка аппроксимации решения достаточно лишь расширить систему линейных алгебраических уравнений дополнительными слагаемыми.
Уравнение нестационарной теплопроводности
Рассматривается одномерное уравнение нестационарной теплопроводности для тонкого однородного стержня с теплоизолированной боковой поверхностью
c T |
|
T W |
(3.18) |
t |
x |
x |
|
с граничными |
|
|
|
T t,0 Q0, |
T t,L Q1 |
(3.19) |
|
x |
|
x |
|
и начальными условиями |
|
|
|
T 0,x T0 . |
|
(3.20) |
|
63

Здесь дополнительно введены обозначения: c – удельная теплоемкость, – плотность материала. Как и ранее, для упрощения W, c, и считаются постоянными величинами.
Весь отрезок длиной L разбивается на ряд равных отрезков длиной h каждый. Решение задачи на произвольном отрезке [xi, xj] строится с помощью разделения переменных в виде
m
Tm t,x Tk t k x .
k 1
Например, для кусочно-линейной аппроксимации это выражение
представляется в форме |
|
|
|
|
|
|
|
|
|
|
Tm t,x Ti t i x Tj t j x . |
(3.21) |
|||||||||
Невязка уравнения (3.18), получаемая на решении |
(3.21), взвешивается с |
|||||||||
весовыми функциями i и j, |
|
|
|
|
|
|
|
|
||
xj |
|
T |
|
|
|
T |
|
|
|
|
|
c |
m |
x |
m W |
idx 0, |
|||||
x |
|
t |
|
|
x |
|
|
(3.22) |
||
xi |
|
Tm |
|
|
|
Tm |
|
|
||
|
j |
|
|
|
W |
|
|
|||
|
|
c |
t |
x |
x |
jdx 0. |
||||
xi |
|
|
|
|
|
|
||||
Выполняются преобразования первого из этих уравнений:
|
|
|
xj |
|
T |
|
|
|
xj |
|
|
T |
|
|
xj |
|
|
|
|
|
|
c |
m idx |
|
|
m idx W idx 0, |
|||||||||||
|
|
|
x |
|
|
t |
|
|
|
x |
x |
x |
|
|
x |
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
xj |
|
T |
|
|
xj |
|
|
|
T |
|
|
|
xj |
T |
|
xj |
||
c |
|
m idx |
x |
|
m |
i dx |
m |
|
i dx W idx 0, |
|||||||||
x |
|
|
t |
|
|
x |
|
|
x |
|
|
|
x |
x |
x |
x |
||
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
i |
|
xj |
T |
idx |
T |
|
xj |
xj |
T |
|
|
xj |
|||||||
|
c |
m |
|
m i |
|
m |
|
i dx W idx 0. |
||||||||||
|
x |
t |
|
|
|
|
x |
|
x |
x |
x |
x |
|
x |
||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
Учитывая, как и ранее, что |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Tm |
|
qi , |
Tm |
|
qj , |
i xi 1, |
i xj 0, |
||||||||
|
|
|
x |
x |
|
|
|
|
|
x |
x |
j |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
последнее соотношение приводится к виду
xj |
T |
xj |
T |
|
xj |
|
qi c |
m idx |
m |
|
i dx W idx 0. |
||
x |
t |
x |
x |
x |
x |
|
i |
|
i |
|
|
|
i |
64
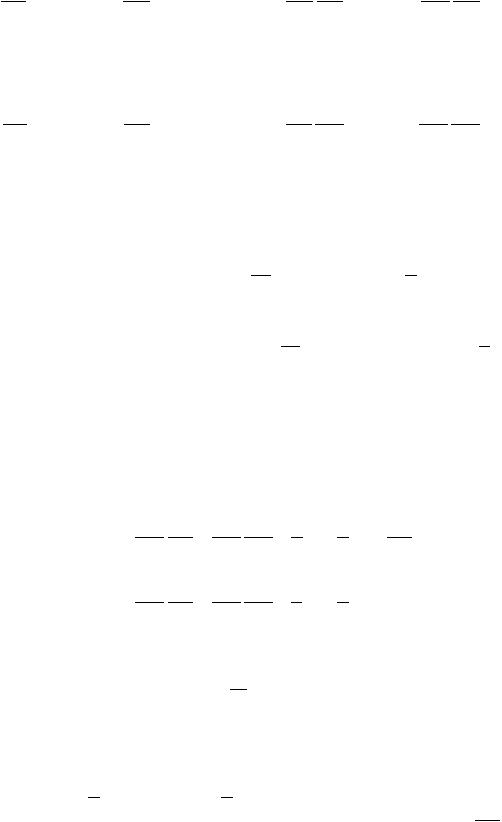
|
Подстановка разложения (3.21) приводит к выражению |
|
|
||||||||||
qi |
dT |
xj |
dTj |
xj |
xj |
d |
|
d |
|
xj |
d j d |
|
xj |
i c i idx |
dt |
c j idx Ti |
|
i |
|
i dx Tj |
|
i dx W idx 0. |
|||||
|
dt |
x |
x |
x |
dx |
dx |
x |
dx dx |
x |
||||
|
|
i |
|
i |
i |
|
|
|
|
i |
|
|
i |
Аналогичные преобразования второго уравнения системы (3.22) приводят к соотношению
qj |
dT |
xj |
dTj |
xj |
xj |
d |
d j |
xj |
d j |
d j |
xj |
|
|
i c i jdx |
dt |
c j jdx Ti |
i |
dx Tj |
|
dx |
dx W jdx 0. |
||||
|
dt |
|
x |
x |
x |
dx dx |
x |
dx |
x |
|||
|
|
|
i |
|
i |
i |
|
|
i |
|
|
i |
В сравнении с системой уравнений (3.5) и (3.6) последние выражения содержат дополнительные слагаемые, которые определяются с учетом вида
функций i |
xj |
x |
h и j |
x xi |
h: |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
xj |
|
idx c2 |
xj |
|
|
|
|
|
|
|
||||
|
|
|
|
|
c i |
xj x 2 dx c h |
, |
||||||||||||
|
|
|
|
|
x |
|
|
|
|
h |
|
x |
|
|
|
|
|
3 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
xj |
c |
|
dx xj |
c |
|
dx c xj |
x |
j |
x x x |
dx c h |
||||||||
|
|
|
i |
j |
|
|
j |
i |
|
|
|
h |
2 |
|
|
|
i |
, |
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
6 |
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
xj |
|
jdx |
c xj |
|
|
|
|
2 |
h |
|||||
|
|
|
|
|
c j |
h |
2 |
x xi |
|
dx c . |
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
3 |
||
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
Теперь система обыкновенных дифференциальных уравнений относительно узловых значений температуры Ti(t) и Tj(t) имеет вид:
c h dT |
c h dTj |
|
|
T |
|
T |
|
|
Wh |
q |
, |
||||
|
|
i |
|
|
|
|
j |
|
|||||||
3 |
dt |
6 |
dt |
|
h |
i |
h |
|
|
2 |
i |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
c h dTj |
|
|
|
|
|
|
|
|
|
|
|
|
c h dT |
|
|
T |
|
T |
|
|
Wh |
q |
|
. |
||||
|
|
i |
|
|
|
|
j |
|
|
||||||
6 |
dt |
3 |
dt |
|
h |
i |
h |
|
|
2 |
j |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
Удобно полученную систему уравнений представить в матричной форме
C d T T W . |
(3.23) |
dt
Здесь использованы матричные обозначения:
h 2 |
1 |
|
1 1 |
Ti |
||||
C c |
|
, |
|
1 |
, |
T |
, |
|
6 |
1 |
2 |
|
h |
1 |
Tj |
||
Wh |
q |
|
|
1 |
|
W 2 |
|
. |
Wh |
qj |
|
|
||
2 |
|
|
Для интегрирования системы обыкновенных дифференциальных уравнений (3.23) могут быть использованы схемы
65

– явная
C Tˆ T T W ,
– неявная
C Tˆ T Tˆ W ,
– Крэнка-Николсона
C Tˆ T Tˆ T W .
2
Последняя разностная схема в виде системы линейных алгебраических уравнений
|
1 |
C |
1 |
|
|
1 |
C |
1 |
|
|
|
2 |
Tˆ |
|
2 |
T W |
|||
|
|
|
|
|
|
||||
наиболее часто используется при решении прикладных задач нестационарной теплопроводности. Использование процедуры ансамблирования для всех конечных элементов, аппроксимирующих рассматриваемый стержень, позволяет исключить внутренние неизвестные тепловые потоки qi и qj.
Контрольные вопросы и задания
Объясните, в чем заключается причина некорректности постановки задачи (3.0) – (3.1).
Опишите порядок построения разрешающих соотношений метода взвешенных невязок для стационарного уравнения теплопроводности.
Покажите, что системы уравнений (3.15), (3.16) и (3.17) имеют определители, равные нулю.
Поясните, почему при использовании иерархической системы функций в системах уравнений (3.15), (3.16) и (3.17) отсутствуют длины h конечных элементов?
С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения стационарной теплопроводности с использованием кусочно-линейной аппроксимации решения.
С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения стационарной теплопроводности с использованием кусочно-квадратичной аппроксимации решения.
Прокомментируйте процесс ансамблирования конечных элементов на примере стационарной задачи теплопроводности. Как учитываются
66
граничные условия I, II и III рода при получении разрешающих соотношений?
Сопоставьте варианты разрешающих соотношений, полученных на основе метода Галеркина, с использованием кусочно-линейной и кусочно-квадратичной аппроксимаций. Укажите достоинства и недостатки того и другого способов аппроксимации.
С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения нестационарной теплопроводности с использованием кусочно-линейной аппроксимации решения.
С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения нестационарной теплопроводности с использованием кусочно-квадратичной аппроксимации решения.
Укажите недостатки и достоинства приведенных в тексте схем аппроксимации производных по времени. Предложите иные разностные схемы аппроксимации производной по времени.
67

4 . З А Д А Ч И М Е Х А Н И К И Д Е Ф О Р М И Р У Е М О Г О Т В Е Р Д О Г О Т Е Л А
Постановка задачи
Пусть равновесное состояние тела (в рамках гипотезы о малых
деформациях) описывается системой уравнений равновесия |
|
|
|
||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
(4.0) |
|
|
F 0, |
x , |
|
|
|
||||||||
физических |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
~ |
, |
|
|
|
|
(4.1) |
||
D |
RT |
x , |
|
|
|
||||||||
геометрических |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
1 |
|
T |
|
, |
|
|
|
|
(4.2) |
||
|
2 |
u u |
|
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
c силовыми |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
F |
|
|
|
(4.3) |
||||
|
n |
F, |
x |
|
|
|
|
||||||
и кинематическими граничными условиями |
|
|
|
|
|
|
|
||||||
|
|
u U, |
x . |
|
|
|
(4.4) |
||||||
|
|
|
|
|
|
|
|
U |
|
|
~ |
~ |
|
Здесь обозначено: |
– |
|
оператор |
|
|
1 |
; |
||||||
|
|
Гамильтона |
, |
|
– тензоры |
||||||||
напряжений и малых деформаций; u – вектор перемещений; n – вектор внешней нормали к поверхности; F, F – векторы массовых и поверхностных
~ ~
сил; D, R – тензоры физико-механических свойств; T – температурное поле; –
плотность материала. Вся поверхность Г тела разделена на ГF , где заданы поверхностные нагрузки, и ГU, на которой заданы кинематические граничные
условия, |
, |
_ |
. |
||
F |
U |
|
Разрешающие соотношения метода взвешенных невязок
1 Гамильтон Уильям Роуан [4.8.1805 – 2.9.1865] – ирландский математик и астроном, член Ирландской королевской академии наук. С 1827 года – профессор астрономии в Дублинском университете и директор университетской астрономической обсерватории. В 1833-35 годах опубликовал работу, в которой дал точное формальное изложении теории комплексных чисел. Построил числовую систему кватернионов, которая явилась одним из источников развития векторного исчисления. В механике предложил метод, названный
принципом наименьшего действия. В 1837 году избран иностранным членом-
корреспондентом Петербургской академии наук.
68

Уравнение равновесия
Поскольку уравнение (4.0) векторное, решением его является векторная функция, а значит, для разложения его в ряд необходимо построить систему векторных пробных функций. Предположим, что i , i 1,2,... – полная и замкнутая система скалярных функций. Используя эту систему, построим набор векторных пробных функций
1 1, 0, 0 , 2 0, 1, 0 , 3 0, 0, 1 , 4 2, 0, 0 , 5 0, 2, 0 , (4.5)
~
Пусть m – приближенное решение уравнения (4.0). Взвесим невязки, получаемые при подстановке этого решения в уравнение (4.0) и граничное условие (4.3), в соответствии с идеей метода Галеркина, используя систему векторных функций (4.5),
~ |
F kd 0, |
|
m |
||
|
|
F kd 0. |
~ |
|
|
n m |
||
F
С помощью соотношений тензорного анализа []
(4.6)
(4.7)
~ |
k |
~ |
|
~ |
|
|
~ |
k )d |
|
~ |
kd |
k ) k |
, |
( m |
n m |
||||||||
m |
( m |
m |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
и соотношения (4.7) первое слагаемое выражения (4.6) преобразуется к виду
~ ~ ~
m kd ( m k )d k md
~ |
kd k |
~ |
|
k |
~ |
n m |
md F kd |
md . |
|||
F |
|
F |
|
|
|
В результате выполненных преобразований получена ослабленная форма уравнения (4.0)
k |
~ |
|
F kd , |
k 1,m, |
(4.8) |
md F kd |
|||||
|
F |
|
|
|
|
~
поскольку искомая функция m теперь вынесена из-под знака производной. Кроме этого, в выражение (4.8) включены силовые граничные условия (4.3). Перейдем от векторной формы записи к компонентной:
j k |
i qp m gipgqjd Fs k r grsd Ft k l gltd , |
k 1,m, (4.9) |
||
|
F |
|
|
|
где компоненты метрического тензора [] |
|
|
||
|
gij ij |
1, |
j i, |
|
|
|
j i. |
|
|
|
|
0, |
|
|
69

В физических компонентах (обозначены чертой сверху) соотношение (4.9) принимает вид
|
|
1 |
|
|
Hi d |
|
F |
|
d |
|
F |
|
d , |
k 1,m |
. (4.10) |
|
|
j |
k i |
ij m |
H j |
i |
k i |
|
i |
k i |
|
|
|||||
|
|
Hi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
В последнем выражении Hj, j = 1, 2, 3 – коэффициенты Ляме. В декартовой ортогональной системе координат H1 = H2 = H3 = 1. В этом случае выражение (4.10) преобразуется к виду (далее знак черты над символами опущен)
|
|
|
|
k |
|
ij |
d |
F |
k |
d |
|
F |
|
k |
|
d , |
|
k 1,m |
. |
|
|
|||||||||||||||||||||||
|
xj |
|
i |
|
|
|
|
m |
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вектора 1 |
это соотношение записывается в форме |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zx |
|
d |
|
|
|
||||||||||||||||||||||
|
|
|
x |
|
|
1 |
|
x |
|
|
xx |
m |
|
x |
1 |
|
y |
|
|
yx m |
|
x |
|
1 |
|
z |
|
|
m |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
m |
|
y |
|
1 |
|
y |
|
|
yy |
m |
|
|
y |
|
|
1 |
z |
|
|
zy |
m |
|
|
|
|||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
xz |
|
|
|
|
|
|
|
|
|
|
|
zz |
|
d |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
m |
|
z |
|
1 |
|
y |
|
|
yz |
m |
|
|
z |
|
|
1 |
z |
|
|
m |
|
|
|
|||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Fx 1 x Fy 1 y Fz 1 z d Fx 1 x Fy 1 y Fz 1 z d . |
|
|||||||||||||||||||||||||||||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, |
|
что |
|
|
|
|
согласно |
|
|
(4.5) |
|
|
1 x 1, |
|
|
1 y 0, |
1 z |
0, |
||||||||||||||||||||||||||
предыдущее выражение приводится к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
xx |
|
|
1 xy |
|
1 |
xz |
d |
|
Fx |
1d |
|
Fx 1d . |
|
|
||||||||||||||||||||||||||||
|
x |
|
|
m |
|
|
|
y |
|
|
|
|
|
m |
|
z |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогичные преобразования с использованием 2, 3 приводят к соотношениям
|
|
yx |
|
|
|
yy |
|
|
|
1 |
1 |
||||||
|
x |
|
m |
|
y |
|
m |
|
|
|
zx m |
|
zy |
|
|||
|
1 |
1 |
||||||
|
x |
|
|
|
y |
|
m |
|
|
|
|
|
|
1d Fy 1d , |
|
1 |
yz m d Fy |
|||
|
z |
|
F |
|
|
|
|
|
|
1d Fz 1d . |
|
|
1 |
zz m d Fz |
|||
|
z |
|
F |
|
|
Для всей системы функций (4.5) полученные выражения можно записать в
виде
70
