Учебное пособие ТеорМех

Решая эту систему, получаем: XA=102 , YA=YB= 20 + 5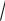2 . Вырежем узел с центром в точке В. В нем сходятся 2 неизвест-

ных усилия: S8 и S9. Составим два уравнения равновесия, приравнивая нулю суммы проекций сил на горизонтальную и вертикальную оси:

-S8 = 0, S9 + YB = 0.

Отсюда: S8 = 0, S9 = −20 − 52 .

Вырежем узел с центром в точке Е. В нем сходятся 2 неизвест-

−10 + 202 .

Продолжая последовательно аналогичные действия, можно определить усилия во всех стержнях фермы.

Для решения поставленной задачи можно применять метод се- чений, называемый методом Риттера. Его алгоритм состоит в сле- дующем.

1.Ферма рассекается сечением, проходящем через стержни фермы, причем суммарное количество неизвестных усилий в рассе- каемых стержнях должно быть не более трех. Сечение также должно проводиться так, чтобы в каждой из частей фермы ока- залось бы не менее двух узлов.

2.Выбирается одна из частей фермы, а другая мысленно отбрасывается; компенсирующие усилия в разрезанных стержнях направляются в сторону отброшенной части.

41

3. Для нахождения некоторого неизвестного усилия состав- ляется уравнение моментов относительно точек, в которых пере- секаются линии действия двух других неизвестных усилий.

Замечание 1. Если два других усилия параллельны, то составля- ется уравнение проекций на ось, им перпендикулярную.

Замечание 2. Отбрасывать целесообразно ту часть, к которой приложено больше активных сил.

Проведем в рассматриваемой ферме сечение, как это показано на рис.3.21, отбросим правую часть фермы и направим усилия в раз- резанных стержнях 1,3,4 в сторону отброшенной части.

Для нахождения усилия S1 составим уравнение моментов отно-

42

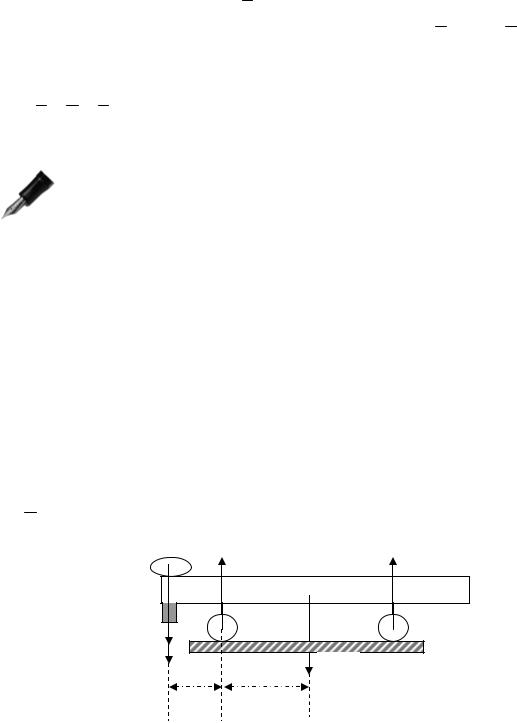
нимается и блок. Запишем уравнение моментов сил относительно точки О.

Так как сила веса груза P проходит через эту точку, то момент этой силы равен нулю, и мы получаем:mO (F) − mO (T) = 0 или Fr − Tr = 0, откуда следует, что F = T . Составим уравнение равнове- сия, приравнивая сумму проекций сил на вертикальную ось:

F + T − P = 0 . Учитывая, что F = T , получаем, что F = P / 2 , то есть подвижный блок дает выигрыш в силе в 2 раза.

На сельскохозяйственных предприятиях часто применяются мобильные передвижные транспортеры, представляющие собой платформу весом G c расположенной на ней транс- портерной лентой, приводимой в движение двигателем ве-

сом P1. Требуется определить, какой максимальный вес груза может переместить транспортер, не перевернувшись.

Очевидно, что самый опасный момент возникает в том случае, когда груз весом P2 расположен в той же точке, где расположен дви- гатель транспортера, как это показано на рис.3.24. В случае опро- кидывания транспортера нормальная реакция N2 обращается в ноль. Уравнение моментов относительно точки, через которую проходит нормальная реакция N1, имеет вид: P1 × a + P2 × a - G × b = 0. Из этого уравнения следует, что вес груза не должен превышать величины

G × ba - P1 .

P1

ab

Рис. 3.24

43

Вопросы для самопроверки:

1.Что называют моментом силы относительно центра?

2.Чему равен главный момент плоской системы сил?

3.Что такое пара сил. Чему равна равнодействующая пары сил?

4.Как определить момент пары?

5.Сформулируйте теорему о главном моменте сил пары (Теоре- ма Вариньона).

6.Какие пары называются эквивалентными?

7.Докажите теорему об эквивалентных парах, лежащих в одной плоскости.

8.Приведите теорему о сложении плоской системы пар.

9.В чем заключается лемма Пуансо (о приведении силы к центру)

10.Сформулируйте основную теорему статики (о приведении системы сил к силе и паре).

11.Каковы условия и уравнения равновесия плоской системы сил?

12.Приведите различные формы уравнений равновесия?

13.В чем заключаются особенности расчета равновесия состав- ных тел?

14.Как определить трение скольжения?

15.Объясните природу возникновения трения качения.

16.Приведите алгоритм расчета узлов фермы методом Риттера.

44

ГЛАВА IV. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

§1. Момент силы относительно центра как вектор

Момент силы F относительно центра О как характеристика ее

вращательного эффекта определяется следующими тремя элементами

знак указывает направление поворота. Но в случае сил, произвольно расположенных в пространстве, плоскости поворота у разных сил бу- дут разными и должны задаваться дополнительно.

Положение плоскости в пространстве можно задать, задав век- тор, перпендикулярный к этой плоскости. Если одновременно модуль

этого вектора выбрать равным модулю момента силы и условиться направлять этот вектор так, чтобы его направление определяло на- правление поворота силы, то такой вектор полностью определит все три элемента, характеризующие момент данной силы относительно центра О.

Поэтому в общем случае момент mo (F) силы F относительно

центра О будем изображать приложенным в центре О вектором Mo , равным по модулю (в выбранном масштабе) произведению модуля силы F на плечо h и перпендикулярным к плоскости ОАВ, проходящей через центр О и силу F. Направлять вектор Mo

будем в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки.

45

Таким образом, вектор Mo будет одновременно характеризовать

модуль момента, плоскость поворота ОАВ, разную для разных сил, и направление поворота в этой плоскости. Точка приложения вектора Mo определяет положение центра момента.

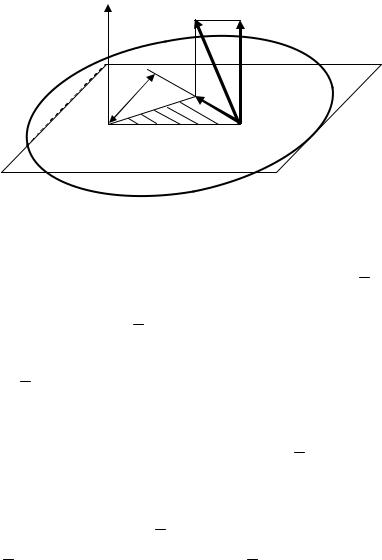
§2. Выражение момента силы с помощью векторного произведения.

Рассмотрим векторное произведение OA × F. Напомним, что

векторным произведением a × b векторов a и b называется вектор c , равный по модулю площади параллелограмма, построен-

ного на векторах a и b , и направленный перпендикулярно плос-

кости этих векторов в ту сторону, откуда кратчайший поворот от a к b виден против хода часовой стрелки.

Следовательно, OA × F = 2пл. OAB = Mo , т.к. модуль вектора Mo тоже равен 2пл. OAB. Направлен вектор ( OA × F) перпендику- лярно к плоскости ОАВ, т.е. так же как и вектор Mo . Значит векторы (OA × F) и Mo совпадают и по модулю и по направлению. Отсюда

Mo = OA × F = r × F ,

где r – радиус-вектор точки А относительно центра О.

§3. Момент пары как вектор

Момент пары (F,F′)изображается вектором m (F,F′), модуль

которого равен произведению модуля одной из сил пары на ее пле-

чо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело про- тив часовой стрелки (рис. 4.2).

m(F,F' )

Рис. 4.2

46

В соответствии с определением модуль момента пары сил m(F,F′) = Fd .

О произвольной системе сил можно доказать теоремы, анало- гичные теоремам, доказанным для системы сил, лежащих в одной плоскости.

Теорема о главном моменте сил пары относительно произвольного центра: главный момент сил пары относительно лю-

бого центра не зависит от выбора этого центра и равен моменту пары, т.е.

Mo = mo (F) + mo (F′) = mo (F, F′) ,

откуда следует, что

mo (F, F′) = mA (F′) + mB (F) .

Теорема об эквивалентных парах: пары, имеющие равные

векторы-моменты, эквивалентны.

Теорема о сложении пар: систему пар в пространстве мож-

но заменить одной парой, момент которой равен векторной сумме моментов данных пар.

Условие равновесия системы пар: для равновесия системы пар в пространстве необходимо и достаточно равенства нулю век- торной суммы моментов этих пар.

Теорема Пуансо: систему сил, как угодно расположенных в

пространстве, можно заменить эквивалентной системой, состоящей из одной силы и одной пары, причем сила равна главному вектору данной системы и приложена в произвольно выбранном центре, а момент пары равен главному моменту системы относительно этого центра.

Условия равновесия произвольной системы сил: для равно-

весия произвольной системы сил необходимо и достаточно, чтобы главный вектор системы и главный момент относительно какого- нибудь центра были равны нулю, т.е.

47

§4. Момент силы относительно оси

Чтобы перейти к решению задач статики для случая произволь- ной пространственной системы сил, необходимо ввести еще понятие о моменте силы относительно оси.

Момент силы относительно оси характеризует вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг дан- ной оси.

Рис.4.3

Рассмотрим твердое тело, которое может вращаться вокруг неко- торой оси z (рис.4.3). Пусть на это тело действует сила F, приложен- ная в точке А. Проведем через точку А плоскость ху, перпендикуляр- ную оси z, и разложим силу F на составляющие: Fz , параллельную оси z, и Fxy , лежащую в плоскости ху (Fxy является одновременно

проекцией силы F на плоскость ху). Сила Fz, направленная парал- лельно оси z, очевидно, не может повернуть тело вокруг этой оси (она только стремится сдвинуть тело вдоль оси z). Следовательно, весь вращательный эффект, создаваемый силой F, будет совпадать с вращательным эффектом ее составляющей Fxy .

Отсюда заключаем, что

mz (F) = mz (Fxy ),

где символ mz (F) обозначает момент силы F относительно оси z. Для силы же Fxy , лежащей в плоскости, перпендикулярной к оси

z, вращательный эффект измеряется произведением модуля этой силы на ее расстояние к от оси. Но этой же величиной измеряется момент силы Fxy относительно точки О, в которой ось z пересекается с плос-

48

костью ху. Следовательно, mz (Fxy ) = mo (Fxy ) или, согласно предыду-

щему равенству

mz (F) = mo (Fxy ) = ±Fxy h

В результате приходим к следующему определению: моментом

силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.

Момент будем считать положительным, если с положительного конца оси z поворот, который сила Fxy стремится совершить, виден

происходящим против часовой стрелки, а отрицательным, если по ча- совой стрелке.

Из рис.4.3 видно, что при вычислении момента по предложенной формуле плоскость ху можно проводить через любую точку оси z. Таким образом, чтобы найти момент силы относительно оси z (рис.4.4), надо:

1)провести плоскость ху, перпендикулярную к оси z (в любом

месте);

2)спроектировать силу F на эту плоскость и вычислить величину

Fxy ,

3)опустить из точки О пересечения оси с плоскостью перпенди- куляр на направление Fxy и найти его длину h;

4)вычислить произведение Fxyh ;

5)определить знак момента.

Z B

F

h FXY

XY 0

Рис.4.4

При вычислении моментов надо иметь в виду следующие част- ные случаи:

- если сила параллельна оси, то ее момент относительно оси ра- вен нулю (так как Fxy = 0).

49

- если линия действия силы пересекает ось, то ее момент относи- тельно оси также равен нулю (так как h = 0).

Объединяя оба случая вместе, заключаем, что момент силы отно- сительно оси равен нулю, если сила и ось лежат в одной плоскости. Если сила перпендикулярна к оси, то ее момент относительно оси ра- вен произведению модуля силы на расстояние между силой и осью.

§5. Условия равновесия произвольной пространственной системы сил

Произвольную пространственную систему сил, как и плоскую, можно привести к какому-нибудь центру О и заменить одной резуль- тирующей силой R и парой с моментом MO . При этом их значения

определяются как

R = åFk , MO = åmO (Fk ).

Поэтому аналогично плоской системе сил можно заключить, что для равновесия произвольной системы сил необходимо и достаточно, чтобы одновременно выполнялись равенства: R = 0, MO = 0. Но век-

торы R и MO могут обратиться в нуль только тогда, когда равны ну- лю все их проекции на оси координат, т. е. когда RX = RY = RZ = 0 и MX = MY = MZ = 0. Или, так как

RX = åFkX , RY = åFkY , RZ = åFkZ ,

MX = åmx (Fk ), MY = åmY (Fk ) , MZ = åmZ (Fk ) ,

когда действующие силы удовлетворяют условиям

Таким образом, для равновесия произвольной пространствен-

ной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

Уравнения (4.1) выражают одновременно необходимые и доста- точные условия равновесия свободного твердого тела, находящегося под действием любой пространственной системы силы. При этом пер- вые три равенства выражают необходимые и достаточные условия того, чтобы тело не имело перемещений вдоль координатных осей, а послед- ние три являются условиями отсутствия вращений вокруг этих осей.

50