
МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ
.pdf
7. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Обыкновенным дифференциальным уравнением называется уравнение
относительно неизвестной функции и ее производных различного порядка
F(x, y, y′, y′′,..., y(n) ) = 0 .
Порядком дифференциального уравнения называется максимальный порядок производной, входящей в него.
Решением дифференциального уравнения называется функция, которая обращает это дифференциальное уравнение в тождество.
Процесс нахождения решения данного дифференциального уравнения называется интегрированием этого уравнения.
Уравнение
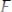








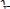









 , связывающее между собой независимую переменную, искомую (неизвест-
, связывающее между собой независимую переменную, искомую (неизвест-
ную) функцию 







 , и ее производную
, и ее производную 








 называется дифференциальным уравнением первого порядка.
называется дифференциальным уравнением первого порядка.
Если это уравнение можно записать в виде




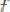










 ,
,
то говорят, что оно разрешимо относительно производной.
Решением (или интегралом) дифференциального уравнения первого порядка
называется любая функция |
|
|
которая при подстановке в это уравне- |
|||
|
||||||
|
|
|||||
ние обращает его в тождество. График функции |
|
|
в этом случае на- |
|||
|
||||||
|
|
|||||
зывается интегральной кривой.
Задача отыскания решения дифференциального уравнения первого порядка, удовлетворяющего заданному начальному условию













 ,
,
называется задачей Коши.
Геометрически это равносильно следующему: требуется найти интегральную
кривую уравнения |
|
|
|
|
|
|
|
|
, проходящую через точку |
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
Общим решением уравнения |
|
|
|
|
|
|
|
называется такая функция |
|||||||||||
|
|||||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где C - произвольная постоянная, что:
1)при любом конкретном значении С она является решением этого уравнения;
2)для любого допустимого начального условия 












 , в окрестно-
, в окрестно-
сти которого существует решение, найдется такое значение постоянной
, что |
|
|
|
. |
|
|
161

В некоторых случаях общее решение дифференциального уравнения приходится записывать в неявном виде:


















 .
.
Тогда соотношение |
|
|
называется общим интегралом этого |
|
уравнения.
Геометрически общий интеграл представляет собой семейство интегральных кривых на плоскости Оху.
Частным решением дифференциального уравнения первого порядка называется функция














 ,
,
получаемая из общего решения |
|
|
|
|
|
|
при конкретном значении по- |
|
|
|
|||||
|
|
|
|
|
|
стоянной |
. |
|
|
Уравнения с разделяющимися переменными. Уравнение вида |
′ |
= f1(x) f2 (y), |
|
y |
|||
где f1 (x) и f2 (y) − непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
Для отыскания решения такого дифференциального уравнения нужно:
1) y′ заменить dy ;
dx
2) разделить переменные (преобразовать уравнение таким образом, чтобы в левой части содержались функция и дифференциал, например, переменной x , а в правой – функция и дифференциал, например, переменной y ).
y′ = f1 (x) f2 (y)
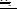



















 ,
,













 ,
,


 .
.
Дифференциальное уравнение с разделяющимися переменными может быть задано в следующем виде:
f1 (x) ϕ1 (y)dx + f2 (x) ϕ2 (y)dy = 0
Разделим обе части уравнения на ϕ1 (y) ≠ 0 и f2 (x) ≠ 0, получим





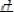















 ,
,
∫f1 (x) dx + ∫ϕ2 (y) dy = С . f2 (x) ϕ1 (y)
Пример 1. Решить дифференциальное уравнение y′ = y .
x
162

dy = y , dx x
dx = y dx : y ≠ 0, x
∫ dyy = ∫ dxx ,
ln y = ln x + ln C1 , ln y = ln C1x ,
y = Cx.






 - общее решение уравнения.
- общее решение уравнения.
Пример2. Решить задачу Коши:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Разделим обе части уравнения на |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
. Получим |
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Интегрируя обе части этого уравнения, получим общий интеграл: |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Отсюда |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( |
, так как рассматриваются только арифметические значения корня.) |
||||||||||||||||||||||||||||||||||||||||||||||||||
Частное решение получим из условия |
|
при |
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Подставляя эти значения х и у в общий интеграл, получим
и частным решением будет














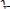





 .
.
Однородные дифференциальные уравнения. Функция F(x; y) называется однородной степени (порядка) k , если при любом t выполняется тождество
F(tx;ty) = tk F(x; y).
F1 (x; y) = x + 2y,
F1 (tx;ty) = tx + 2ty = t (x + 2y) = t F1 (x; y) F1 (x; y)
- однородная функция первой степени.
163

F |
(x; y) = x2 sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
tx |
|
|
x |
|
|
|
F |
(tx;ty) = (tx)2 sin |
|
= t2 x2 |
sin |
|
|
= t2 F (x; y) F (x; y) |
|||
|
|
|||||||||
2 |
|
|
|
ty |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
y |
|
|
||
- однородная функция второй степени. Дифференциальное уравнение I порядка
называется однородным, если |
P(x; y) и Q(x; y) − однородные функции одной и |
||||||||||||||||
той же степени k. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это уравнение может быть приведено к виду |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Способ решения. Введем вспомогательную функцию |
z(x) = |
|
, z = |
|
|
, тогда |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
подставляя в уравнение, получим











 .
.
Откуда








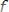








 ,
,


















 ,
,


















 ,
,
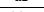

 .
.
Интегрируя, получим




 ,
,
Решив полученное уравнение относительно z, делаем замену z = y и выра-
x
жаем функцию y.
Пример 3. Найти общее решение дифференциального уравнения y′ = x2 + y2
2xy
Функции, стоящие в числителе и знаменателе, однородные II степени, данное уравнение является однородным.
Введем новую функцию z = |
y |
|
′ |
′ |
|
, |
|||||
y = zx, y |
= z x + z. |
||||
|
x |
|
|
||
164
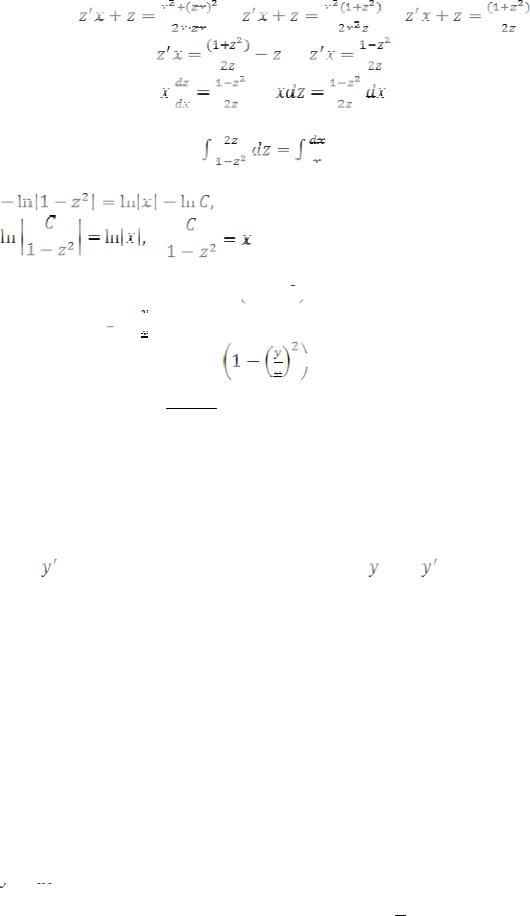
Получим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Разделяя переменные и интегрируя, получим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или
















 .
.
Подставляя 




 , получим
, получим






 ,
,
= С - общее решение уравнения.
Линейные уравнения первого порядка. Линейным дифференциальным уравнением I порядка называется уравнение вида
y′ + p(x)y = f (x) .
Способ решения. Если f (x) ≠ 0, то решение уравнения будем искать в виде
y = u v |
(где u и v − функции, зависящие от |
x т. е. u = u(x), v = v(x) ). Нахо- |
дим |
и подставляем в уравнение значения |
и : |
|
y′ = u′v + uv′, |
|
|
u′v + uv′ + p(x) uv = f (x), |
|
|
u′v + u (v′ + p(x) v) = f (x), |
(*) |
Выберем функцию v такую, чтобы выражение в скобках v′ + p(x) v = 0 . Тогда
уравнение (*) сведется к системе двух дифференциальных уравнений. |
|
v′ + p(x) v = 0 1) |
|
u′v = f (x) |
2) |
|
|
Решим уравнение (1) системы: v′ + p(x) v = 0 ,
Имеем линейное однородное дифференциальное уравнение I порядка, которое является уравнением с разделяющимися переменными. Находим из этого уравнения функцию v, подставляем ее значение во второе уравнение и определяем функцию u. Запишем общее решение исходного уравнения в виде







 .
.
Пример 4. Найти общее решение уравнения y′ + 2 y = x.
x
165

Будем искать решение в виде:
y= uv,
y′ = u′v + uv′,
Подставляя значения y 

 в уравнение, группируя по переменной u, перейдем к системе двух дифференциальных уравнений, каждое из которых является уравнением с разделяющимися переменными, и решим их.
в уравнение, группируя по переменной u, перейдем к системе двух дифференциальных уравнений, каждое из которых является уравнением с разделяющимися переменными, и решим их.
u′v + uv′ + 2 uv = x,
|
|
|
|
x |
|
|
′ |
|
|
′ |
|
2 |
|
|
v |
+ |
|
v = x, |
||
u v + u |
|
|
||||
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
v′ + |
|
v = 0, |
|
(1) |
||
|
|
|||||
|
x |
|
|
|
|
|
u′v = |
x. |
|
|
|
(2) |
|
|
|
|
|
|
|
|
Решим (1) уравнение системы: |
Решим (2) уравнение системы: |
|||||||||||||||||||||||||||||||
|
v′ + |
2 |
v = 0, |
|
|
|
|
u′v = x, |
|
|||||||||||||||||||||||
x |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dv |
= - |
|
2 |
|
v, |
|
|
|
|
|
u′ |
1 |
= x, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
dx |
|
|
|
x |
|
|
|
|
|
|
|
x2 |
|
||||||||||||||||||
|
dv = - |
2 |
|
|
|
|
|
|
|
|
|
|
u′ = x3 , |
|
||||||||||||||||||
|
vdx |
: v, |
|
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dv |
= - |
2dx |
, |
|
|
|
|
|
du |
= x3 |
∫du = ∫x3dx, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
v |
|
|
|
|
|
|
x |
|
|
|
|
|
dx |
|
||||||||||||||||
|
|
ln |
|
v |
|
= -2ln |
|
x |
|
, |
|
u = |
x4 |
|
+ C, |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||
|
|
ln |
|
v |
|
= ln |
1 |
|
, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
v = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||









 - общее решение уравнения.
- общее решение уравнения.
Уравнения Бернулли. Уравнение вида |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где |
, |
, |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а |
|
|
|
|
|
и |
|
|
|
|
|
|
|
- непрерывные функции, называется уравнением Бернулли. |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
Это уравнение приводится к линейному уравнению с помощью подстановки









 . Уравнение Бернулли можно, не сводя к линейному, проинтегри-
. Уравнение Бернулли можно, не сводя к линейному, проинтегри-
ровать с помощью подстановки 






 (т.е. методом Бернулли) или приме-
(т.е. методом Бернулли) или приме-
нив метод вариации произвольной постоянной (метод Лагранжа).
Уравнения второго порядка, допускающие понижение порядка. Рассмотрим отдельные примеры.
166

1) Уравнение вида F(x; y′′) = 0 или это уравнение может быть записано в виде y′′ = f (x) . В данном уравнении не содержится y и y′ , поэтому решить его можно с помощью двукратного интегрирования.
Пример 5. Найти общее решение уравнения y′′ − sin x = 0 .
Представим 

 как
как 



 , получим
, получим
dy′ = sin x, dx
∫dy′ = ∫sin xdx,
y′ = −cos x + C1,
Заменяем 

 на отношение дифференциалов
на отношение дифференциалов
dy
dx
= −cos x + C1,
∫dy = ∫(−cos x + C1 )dx,
y= −sin x + C1x + C2 .
2)Уравнение вида F(x; y′; y′′) = 0 не содержит переменную y . С помощью
подстановки y′ = z(x) преобразуется в дифференциальное уравнение I порядка.
Если |
y |
′ |
= z(x), |
|
то |
y |
′′ |
|
|
|
′ |
, тогда уравнение примет вид: |
′ |
||||||||||||||||||||||||||||||||||||
|
|
|
= z (x) |
F(x; z; z ) = 0. Решим |
|||||||||||||||||||||||||||||||||||||||||||||
это |
уравнение относительно |
z(x) = ϕ(x;C1),и |
|
найдем |
у из уравнения |
||||||||||||||||||||||||||||||||||||||||||||
y′ = ϕ(x;C1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
= ϕ(x;C ), |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3) Уравнение вида |
|
|
|
|
|
|
не содержит переменную |
х . Введем новую |
|||||||||||||||||||||||||||||||||||||||||
F(y; y ; y ) = 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
функцию z(y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
такую, что z = y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y′′ = |
d(y′) |
= |
dy′ |
|
dy |
= |
dz |
|
dy |
= |
dz |
z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
dx |
|
|
|
dy |
|
dx |
|
dy |
|
|
dx |
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Уравнение примет вид F(y; z; z′y ) = 0. |
Решив это уравнение, найдем |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = ϕ(y;C1) y′ = ϕ(y;C1). |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy = ϕ(y;C1)dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
= dx ∫ |
|
|
|
|
|
|
dy |
|
= x + C2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ(y;C ) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ(y; C ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
- общее решение уравнения.
Пример 6. найти общее решение дифференциального уравнения:
167
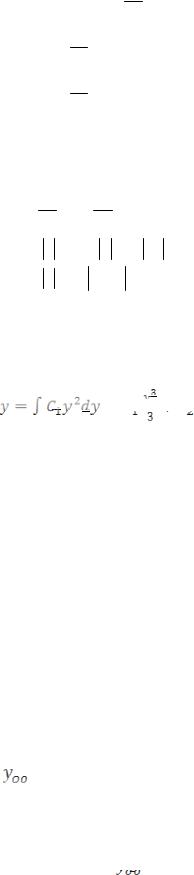
y y′′ − 2(y′)2 = 0,
y′ = z, y′′ = dz z, dy
y z dz − 2z2 = 0, dy
y z dz = 2z2 , dy
y z dz = 2z2dy,
Разделяя переменные и интегрируя, получим
∫ dzz = 2∫ dyy ,
ln z = 2ln y + ln C1 , ln z = ln C1 y2 ,
z = C1 y2 , y′ = C1 y2 .
Интегрируя последнее равенство, найдем общее решения уравнения у.





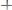



 .
.
Линейные дифференциальные уравнения II порядка с постоянными коэффициентами. Линейным дифференциальным уравнением II порядка с постоянными коэффициентами называется уравнение вида:
y′′ + py′ + qy = r(x) ,
Если r(x) = 0, то уравнение y′′ + py′ + qy = 0 называется линейным однородным дифференциальным уравнением II порядка с постоянными коэффициентами.
Общее решение линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами ищется с помощью характеристического уравнения k 2 + pk + q = 0 . Характеристическое уравнение получается
из уравнения y′′ + py′ + qy = 0 |
заменой y′′ → k2, y′ → k, y → k0. Т. к. характери- |
|
стическое уравнение квадратное, то оно имеет не более двух корней. |
||
Справедливо утверждение: |
|
|
1) |
если корни характеристического уравнения действительны и различны, |
|
k1 |
≠ k2 , то общее решение |
однородного уравнения y′′ + py′ + qy = 0 имеет |
вид:
yoo = C1ek1x + C2ek2x
2)если корни характеристического уравнения действительны и равные,
k1 = k2 = k, то общее решение уравнения 


 имеет вид:
имеет вид:
yoo = C1ekx + C2 xekx
168

3) если характеристическое уравнение не имеет действительных корней, то общее решение уравнения 



 имеет вид:
имеет вид:
|
|
|
|
y |
|
= eαx (C cos βx + C |
|
sin βx), где α = − |
p |
, |
β = |
q − |
p2 |
. |
|
|
|
||||||
|
|
|
|
oo |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 7. Найти общее решение следующих уравнений: |
|
|
|||||||||||||||||||||
а) y′′ + y′ − 2y = 0 |
|
б) y′′ − 2y′ + y = 0 |
|
|
в) y′′ − 4y′ +13y = 0 |
||||||||||||||||||
k 2 + k − 2 = 0 |
|
|
k 2 − 2k +1 = 0 |
|
|
k 2 − 4k +13 = 0 |
|
|
|||||||||||||||
D = 1+ 8 = 9 |
|
|
|
(k −1)2 = 0 |
|
|
|
D = (−4)2 − 4 13 = −36 < 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k1 = −2, k2 = 1 |
|
|
k1 = k2 = 1 |
|
|
|
α = 2, β = 13 − 4 = 3 |
|
|||||||||||||||
y |
oo |
= C e−2x |
+ C |
ex |
y |
oo |
= C ex + C |
2 |
xex |
y |
oo |
= e |
2x (C cos3x + C |
2 |
sin3x) |
||||||||
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||
Решение неоднородных уравнений II порядка с постоянными коэффициента-
ми y′′ + py′ + qy = r(x) .
а) Метод вариации произвольной постоянной.
Находим общее решение соответствующего однородного уравнения в виде y = C1 y1 + C2 y2 ,
где y1 и y2 − функции, зависящие от x .
Предполагаем, что C1 и C2 − функции от переменной x, т. е.
y = C1 (x)y1 + C2 (x)y2
Функции C1(x) и C2 (x) , находятся из системы дифференциальных уравнений
C1′y1′ + C2′ y2′ = 0,
C1′y1′ + C2′ y2′ = r(x).
Решив эту систему, в которой C1 и C2 неизвестные, а y1 и y2 ; |
y1′ и y2′ − ко- |
|||||||
эффициенты найдем C1 и C2 , а следовательно и общее решение данного |
||||||||
уравнения. |
|
|||||||
Пример 8. Найти общее решение уравнения |
|
|
|
. |
||||
|
||||||||
|
|
|
||||||
|
|
|
||||||
Рассмотрим линейное однородное дифференциальное уравнение |
|
|||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
составим соответствующее характеристическое уравнение и найдем его общее решение.
k 2 + 2k +1 = 0 k1 = k2 = −1
yoo = C1e−x + C2 xe−x
Будем искать общее решение данного уравнения в виде:
y = C1 (x)e−x + C2 (x)xe−x .
Запишем систему дифференциальных уравнений и решим ее.
C′e |
− x + C′ xe− x = 0, |
C′ + C′ x = 0, |
|||||
|
1 |
2 |
(e−x − xe−x ) = e−x . |
|
1 |
2 |
1− x) = 1. |
C′e |
−x + C′ |
|
− C′ + C′ |
||||
|
1 |
2 |
|
1 |
2 |
|
|
Получим
169

|
|
|
, |
откуда |
C = − |
x2 |
+ D . |
|
|||||||
|
|
|
|
||||
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
, |
|
|
|
откуда |
C2 = x + D2 . |
||
Таким образом, общее решение исходного уравнения имеет вид:
|
|
x |
2 |
|
|
|
y = |
− |
|
+ D |
e−x + (x + D )xe−x . |
||
|
|
|||||
|
2 |
1 |
|
2 |
||
|
|
|
|
|||
б) Метод неопределенных коэффициентов.
Общее решение линейного неоднородного уравнения находится так:
1.Найти общее решение соответствующего однородного уравнения 




 .
.
2.Найти одно какое-нибудь частное решение 
 .
.
3.Общее решение найти как сумму этих двух решений: 









 .
.
Рассмотрим случай, когда правая часть уравнения имеет специальный вид













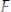






 .
.
y′′ + py′ + qy = r(x)
Частное решение |
|
|
будем искать в виде г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где k |
число |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
совпадений |
|
|
|
с корнями характеристического уравнения; |
|
|
|
|
- |
|
много- |
||||||||||||||||||||||||||||
член с неопределенными коэффициентами той же степени, что и |
|
|
|
|
. |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
Способ решения заключается в следующем: найти |
|
|
|
|
и |
|
|
, подставить зна- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
чения |
|
, |
|
, |
|
|
|
|
в данное уравнение, и методом неопределенных коэффици- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
ентов найти значения коэффициентов многочлена |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пример 9. Найти общее решение уравнения y′′ − 2y′ + y = x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1)ищем общее решение соответствующего однородного уравнения:
y′′ − 2y′ + y = 0 k2 − 2k +1 = 0 k1 = k2 = 1
yoo = C1ex + C2 xex .
2)частное решение ищем в виде 



















 .
.
Так как правая часть исходного уравнения |
y′′ − 2y′ + y = x2 не содержит мно- |
||||||||||||
житель |
|
|
|
, следовательно, |
|
, и |
|
|
|
|
, т.е. совпадений |
|
с |
|
|||||||||||||
|
|
|
|||||||||||
корнями характеристического уравнения нет, то получим k = 0.
В правой части исходного уравнения стоит многочлен второй степени, значит








 запишется в виде
запишется в виде




















 .
.
Таким образом, частное решение 
 запишется как
запишется как








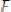




 .
.
Находим 

 и
и 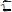

 :
:
|
|
|
|
|
|
|
|
, |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Подставляем в уравнение значения |
|
, , |
|
, получим |
||||||||||
|
|
|||||||||||||
170
