01_Физические_основы_механики

εz = ddtωz .

Проекция углового ускорения на ось вращения равна производной по времени проекции угловой скорости на эту же ось. Ес-

ли εz >0 , то модуль вектора ω возрастает, при εz < 0 , модуль ωr убывает.

1.16.Уравнение кинематики для вращения твердого тела вокруг неподвижной оси

Основная задача кинематики при вращении твердого тела вокруг неподвижной оси заключается в нахождении зависимости от времени угла поворота и модуля угловой скорости

ϕ =ϕ(t), ω =ω(t).

Равнопеременное вращение

Вращение твердого тела называется равнопеременным, если угловое ускорение остается постоянным по направлению и величине с течением времени ε = const . Из этого условия следует,

что ε = const,εz = const .

Запишем два уравнения

εz = ddtωz , ωz = ddtϕ .

Перепишем их

dωz =εz dt, dϕ =ωz dt.

Величина dωz есть приращение проекции угловой скорости

на ось вращения за элементарный промежуток времени dt . Величина dϕ есть приращение угла поворота тела за тот же элемен-

тарный промежуток времени dt .

Рассмотрим вращение тела за промежуток от нулевого момента времени до момента t. Пусть в нулевой момент выполняются

40

условия ωz (0) = ωz0 ,ϕ(0) = 0 . Разобьем интервал времени от 0 до t на очень большое число элементарных интервалов времени dt . В течение i-го интервала проекция угловой скорости и угол поворота получают приращения

dωzi =εzi dti , dϕi =ωzi dti .

Значения ωz и ϕ в момент t найдем следующим образом:

ωz (t) =ω0 z + ∫εz dt , ϕ(t) = ∫ωz dt .

Из первого интеграла при εz = const получаем

ωz (t) = ωoz +εzt .

Подставим это значение во второй интеграл:

Часто при этом индекс «z» не пишут. Кроме того, очевидно, что εz может иметь следующие значения:

εz = ±εr = ±ε ,

где ε – модуль углового ускорения. Запишем

ω(t) =ω0 ±εt , ϕ(t) =ω0t ± εt2 .

2

Здесь ω0 – величина угловой скорости в нулевой момент вре-

мени; ω – величина угловой скорости в момент времени t ; «+» – равноускоренное вращение, при котором угловая скорость возрас-

41

тает; «–» – равнозамедленное вращение, при котором угловая скорость убывает; ϕ – угол поворота в момент времени t .

Равномерное вращение

Вращение называется равномерным, если угловая скорость

остается неизменной по величине и направлению

ω =const, ω =const.

Запишем

ω(t) = ω0 ±εt .

Очевидно, что для того, чтобы ω = const , необходимо ε = 0 . Тогда

ω(t) =ω0 =ω , ϕ(t) =ω0t ± εt 2 =ωt .

2

Возьмем приращение от обеих частей второго уравнения: ∆ϕ = ω∆t. Обозначим

∆t =T, ∆ϕ = 2π ,

где Т – интервал времени, за который приращение угла ϕ состав-

ляет 2π радиан. Запишем

2π =ω T , ω = 2Tπ .

Величина T имеет смысл промежутка времени, за которое тело совершает один оборот вокруг оси вращения. Величина T называется периодом вращения. Величина, обратная периоду вра-

щения, называется частотой вращения n = T1 , обс = 1с.

Частота вращения численно равна числу оборотов в единицу времени.

Запишем

ω = 2Tπ = 2πn , ϕ =ωt = 2πnt , 2ϕπ = nt = N ,

42

где N – количество оборотов, которое тело совершает за время t .

1.17.Связь между линейными и угловыми характеристиками движения

Движение частицы твердого тела можно характеризовать величинами V , ar, arn , arτ и ω,ε .

Величины V , ar, arn , arτ называются линейными, а ω,ε – угло-

выми характеристиками движения. Найдем связь между ними. Проведем из произвольной точки на оси вращения радиус-

вектор в точку М. За время dt точка, двигаясь по окружности радиуса R, совершаетr элементарное перемещение dr .

Модуль dr равен

V =ω r sinθ =ωR .

Все точки твердого тела имеют одну и ту же угловую скорость. Линейная скорость точек зависит от их расстояния от оси вращения.

43

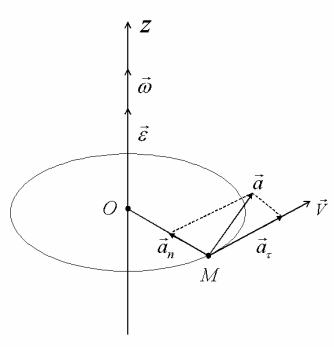
Рис. 1.16. Линейные и угловые характеристики движения материальной точки

Определим модуль и направление каждого векторного слагаемого. Вектор [ε ×rv] перпендикулярен векторам ε и r , и по правилу векторного произведения направлен вдоль вектора ско-

рости V . Следовательно, первое слагаемое есть тангенциальное

ускорение точки М:

arτ =[εr×rr], aτ =εr sinθ, aτ =εR.

44

Для модуля второго слагаемого запишем

Вектор направлен вдоль радиуса rк центру окружности, т.е.

перпендикулярно к вектору скорости V . Следовательно, этот вектор есть нормальное ускорение точки

Полное ускорение равно по величине a = (εR)2 + (ω2 R)2 .

Рис. 1.17. Расчет полного ускорения материальной точки

45

Глава 2. Динамика материальной точки

Динамика – раздел механики, изучающий движение тел с учетом причин возникновения и изменения движения. В основе классической динамики материальной точки лежат три закона Ньютона.

2.1. Первый закон Ньютона (закон инерции)

Для описания движения необходимо выбрать определенную систему отсчета. Кроме того, известно, что в различных системах отсчета движение в общем случае выглядит по-разному. Возникает задача выбора такой системы отсчета, в которой законы механики будут более простыми. Оказывается, что такие системы отсчета существуют и обладают следующим важным свойством: тело, на которое не действуют другие тела, движется в указанной системе прямолинейно и равномерно или по инерции. Соответственно, систему отсчета называют инерциальной. Утверждение, что инерциальные системы существуют, составляет суть первого закона Ньютона или закона инерции.

Существуют системы отсчета, называемые инерциальными, в которых всякое тело находится в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Оба указанных состояния (покоя и равномерного прямолинейного движения) характеризуются тем, что ускорение тела равно нулю. Существование инерциальных систем неочевидно, однако подтверждается опытом. С очень высокой степенью точности инерциальной является т.н. гелиоцентрическая система отсчета, связанная с Солнцем. Во многих случаях с достаточной степенью точности можно считать инерциальной систему отсчета, связанную с Землей. Системы отсчета, не являющиеся инерциальными,

называются неинерциальными.

2.2. Второй закон Ньютона

Из опыта известно, что если на тело не оказывается никакого воздействия, то оно сохраняет состояние покоя или равномерного и прямолинейного движения сколь угодно долго. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.

46

Из опыта известно, что некоторые тела оказывают действие на другие тела. Количественная характеристика действия одного тела на другое называется силой. Результат действия зависит как от его интенсивности, так и от направления воздействия и точки приложения. Это указывает на то, что сила является векторной величи-

ной. Будем обозначать силу F . Из опыта известно, что если на некоторое тело действует сила, то скорость тела при этом изменяется в соответствии с законом

Fdt = mdV ,

где dt – время действия силы, dV – приращение скорости тела в результате действия силы.

Постоянная для данного тела величина m называется инертной массой (массой) и является количественной мерой инертности тела: m, кг. Из опыта известно, что масса тела оказывается одной и той же независимо от того покоится тело или движется: m = const . Запишем

Fdt = mdV = d(mV ) .

Импульсом тела называется вектор, равный pr = mVr, p = mV , кгсм.

Связь силы и изменения импульса определяется вторым за-

коном Ньютона.

В инерциальной системе отсчета производная от импульса материальной точки по времени равна силе, действующей на материальную точку

F = ma, кгс2 м = Н, Ньютон.

Произведение массы материальной точки на ее ускорение равно силе, действующей на материальную точку.

47

2.3. Третий закон Ньютона

Во всех случаях, когда в опыте участвуют только два тела, например 1 и 2, и тело 1 сообщает ускорение телу 2, обнаруживается, что и тело 2 сообщает ускорение телу 1. Это означает, что действие тел друг на друга имеет характер взаимодействия. Третий закон Ньютона определяет общее свойство всех сил взаимодействия.

Силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки

F12 = −F21 , F12 = F21 .

Рис. 2.1. Взаимодействие материальных точек

В третьем законе Ньютона предполагается, что обе силы равны в любой момент и независимо от движения тел.

2.4. Сложение сил

Пусть на материальную точку одновременно действуют несколько сил F1 , F2 ,..., Fi ,..., Fn в результате чего частице сообщается ускорение a . Пусть на эту же частицу действует одна си-

щает частице такое же ускорение a , как и n сил. Действие нескольких сил, приложенных одновременно к одной и той же материальной точке, эквивалентно действию одной силы, равной геометрической сумме всех приложенных сил

i=1

48

Этот экспериментально установленный факт называется принципом суперпозиции сил. С учетом принципа суперпозиции второй закон Ньютона записывается так:

Произведение массы материальной точки на её ускорение равно геометрической сумме всех сил, действующих на эту точку.

2.5. Законы сил

Для применения второго закона Ньютона необходимо знать явное выражение для силы или закон силы.

Сила тяжести

Между двумя материальными точками действует сила грави-

тационного притяжения, определяемая законом всемирного

тяготения

F12 = F21 = F =γ mr1m2 2 , γ = 6,67 10−11 , Нмкг22 .

Рис. 2.2. Гравитационное взаимодействие материальных точек

Коэффициент γ называется гравитационной постоянной.

Пусть материальная точка находится на расстоянии h над поверхностью Земли.

В этом случае сила, действующая на частицу со стороны Земли, равна