Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский государственный технический университет

Предмет:

Высшая математика

Файл:

Методичка по математике.1 курс.1 семестр.ФЭИС

.pdf

Скачиваний:

253

Добавлен:

01.03.2016

Размер:

566.31 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

161. Составить уравнение гиперболы, фокусы которой принадлежат оси абсцисс и симметричны относительно начала координат, если:

а) 2c =10; 2b = 8;

б) 2a =16; ε = 54 ;

в) 2c =12; ε = 56 ;

г) ее фокусы лежат на оси Оу, расстояние между ними равно 20, а действительная ось равна 16;

д) уравнение асимптот y = ± 34 x , расстояние между директрисами

равно 12,8.

162. Установить, какие кривые задаются следующими уравнениями:

а) 16x2 − 25y2 + 32x −100y + 84 = 0;			б) 5x2 −9y2 −30x +18y −9 = 0 ;

в) x = 9 − 2	y2 + 4y + 8	;	г) y = −3 x2 +1.

163. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

а) парабола расположена в правой полуплоскости, симметрично относительно оси Ox, и её параметр p = 3 ;

б) парабола расположена симметрично относительно оси Oy и проходит через точку A(4;−8);

в) она симметрична относительно оси Ох и проходит через точку

А(6; –2).

164. Составить уравнение параболы, вершина которой находится в точке A(1;− 2), если парабола расположена:

а) симметрично относительно прямой x −1 = 0 и проходит через точку

B(2;0);

б) симметрично относительно прямой y + 2 = 0 и проходит через точку

B(2;0).

165. Установить, какая линия определяется уравнением, и изобразить эти линии на чертеже:

а) y	2	+10x + 2y = 0 ;			б) y = −	1	x	2	+ 2x −7 ;
						6

в) 2x2 + 5y2 + 8x −10y −17 = 0 ;					г) x2 −8x + 2y +18 = 0;
							3
д) x = −4 + 3				;	е) y = 7 −					x2 − 6x +13 ;
			y + 5
							2

ж) x = 5 −

y2 + 4y −12 ;

з)

y = −5 +

−3x − 21

;

и)

y =1−

−6x − x2 ;

к)

x = −2 +

−5 − 6y − y2

Задания для индивидуальной работы

166.Найти уравнение окружности, если концы одного из ее диаметров находятся в точках A(3;9), B (7;3).

167.Найти уравнения касательных, проведенных из точки M(0;3) к ок-

ружности x2 + y2 − 6x + 4y −12 = 0 .

Ответ: y = 3; y = 158 x + 3 .

168. Записать уравнение окружности, если:

а) она проходит через правый фокус гиперболы 57x2 − 64y2 = 3648 и ее центр в точке А(2; 8);

б) она проходит через левый фокус эллипса 13x2 + 49y2 = 837 и ее

центр в точке А(1; 8); в) она проходит через точку В(3; 4) и ее центр в вершине параболы

y2 = 41 (x + 7);

г) она проходит через фокусы гиперболы 4x2 −5y2 = 20 и ее центр в

точке А(0; –6).

169. Составить каноническое уравнение эллипса, если:

а) малая ось равна 24, расстояние между фокусами равно 10; б) расстояние между фокусами равно 6, эксцентриситет равен 35 ;

в) расстояние между директрисами равно 32, эксцентриситет равен

0,5;
г) малая полуось равна 7 и	один из фокусов		находится в точке
F (13; 0);
		40
д) эллипс проходит через точки	A(−3; 0), B 1;	40	;
д) эллипс проходит через точки	A(−3; 0), B 1;		;
		3
		3

е) эллипс проходит через точку A(0; − 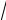11) и ε = 56 ;

ж) большая ось равна 30 и ε = 1517 .

170. Составить уравнение эллипса, фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная, кроме того, что:

а) его полуоси равны, соответственно, 7 и 2; б) его малая ось равна 16, а эксцентриситет равен 0,6;

в) расстояние между его директрисами равно 10 32 , а эксцентриситет равен 0,6.

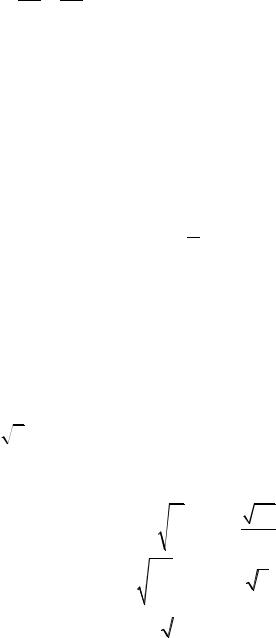
171. Составить уравнение прямой, проходящей через левый фокус и

нижнюю вершину эллипса x2 + y2 =1. 25 16

172. Составить уравнение эллипса, если известны его эксцентриситет ε = 0,5, фокус F(3;0) и уравнение соответствующей директрисы:

x + y −1= 0.

173. На эллипсе найти точку, расстояние до которой от правого фокуса в четыре раза меньше расстояния до левого фокуса, если уравнение эл-

липса 16x2 + 25y2 = 400.

174. Составить каноническое уравнение гиперболы, если: а) действительная полуось a = 4, эксцентриситет ε =1,25;

б) ее асимптоты заданы уравнениями y = ± 2x и расстояние между фо-

кусами равно 10; в) расстояние между вершинами равно 8, расстояние между фокусами

равно 10; г) действительная полуось равна 5, вершины делят расстояние между

фокусом и центром пополам; д) действительная ось равна 6, гипербола проходит через точку

A(9;− 4);

е) точки P (−5;2) и Q (25;1) принадлежат гиперболе;

ж) мнимая полуось равна 4 и один из фокусов находится в точке

F (–11; 0);

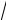з) уравнения асимптот гиперболы y = ±x32 и ε = 153 ;


					(		)
и) гипербола проходит через точки		32
		32		и B		8; 0		;

	A	3	; 1
		3
к) уравнения асимптот гиперболы y = ±x			17	и 2c =18.
к) уравнения асимптот гиперболы y = ±x			8	и 2c =18.
			8

175. Составить уравнение гиперболы, зная, что:

а) расстояние между вершинами равно 24, а фокусы находятся в точ-

ках F1(−10;2) и F2(16;2) ;

б) эксцентриситет равен 54 , один из фокусов находится в точке F(5;0)

и уравнение соответствующей директрисы 5x −16 = 0.

176. Точка M1(1;− 2) лежит на гиперболе, фокус которой находится в точке F(−2;2) , а соответствующая директриса дана уравнением 2x − y −1= 0 . Составить уравнение этой гиперболы.

177.	Дан эллипс	x2	+	y2	=1. Найти уравнение гиперболы, вершины ко-
		15		6

торой находятся в фокусах, а фокусы в вершинах данного эллипса. 178. Составить каноническое уравнение параболы, если:

а) F (0;2) – фокус, O (0;0) – вершина параболы;

б) она симметрична относительно оси Ox и проходит через точки

O (0;0) и M (1;− 4);

в) она симметрична относительно оси Oy и проходит через точки

O (0;0) и N (6;− 2);

г) уравнение директрисы параболы x =13; д) уравнение директрисы параболы y = 4;

е) уравнение директрисы параболы y = −3 ;

ж) она симметрична относительно оси Оу и проходит через точку

А(4; –10).

179.Струя воды фонтана, имеющая форму параболы, достигает наибольшей высоты 4м на расстоянии 0,5м от вертикали, проходящей через точку О выхода струи. Найти высоту струи над горизонталью Ox на расстоянии 0,75м от точки О.

180.Составить уравнение параболы, если её вершина в точке A(2;1) и

уравнение директрисы 2x − y + 2 = 0 .

181.Осевое сечение зеркала-прожектора имеет форму параболы. Определить положение фокуса, если диаметр зеркала 80 см, а глубина 40 см.

182.Установить, какие линии определяются следующими уравнениями. Изобразить их на чертеже.

а) x2 + y2 − 4x + 6y + 4 = 0 ;

б) 2x2 + 5y2 + 8x −10y −17 = 0 ;

в) x2 − 6y2 −12x + 36y − 48 = 0;

г) x2 −8x + 2y +18 = 0;

д) y = −1+

x2 − 4x −5 ;

е) x = 9 − 2 y2 + 4y + 8 ;

з) x = −5 + 2

ж) y = −7 +

−x2 + 6x +16 ;

8 + 2y − y2 ;

и) y = 3 − 4

x −1

;

к) x = 2 −

6 − 2y

;

м) y = 2

л) x = −5

;

+ 25 .

−y

183. Составить уравнение линии, каждая точка которой:

а) отстоит от прямой x = −7 на расстоянии в три раза меньшем, чем от точки А(3; 1);

б) отстоит от прямой x = 2 на расстоянии в пять раз большем, чем от точки А(4; –3);

в) отстоит от прямой x = −1 на расстоянии в четыре раза большем, чем от точки А(1; 5).

г) отношение расстояний от точки М до точек А(3; –5) и В(4; 1) равно

0,25.

Ответы. 155. а) (x −3)2 +

(y +1)2 = 5; б) x2 + y2 = 4.

156. а)

(x − 2)

(y + 4)

+ (y −3)

25 .

36 ; б) x +

158.

(x −1)2

(y + 2)2

=1.

159. а)

=1; б)

=1; в)

=1; г)

=1;

169

д)

=1; е)

=1; ж)

=1.

16 3

41 16

41 25

161. а)

−

=1; б)

−

=1; в)

−

=1; г) −

=1; д)

−

=1.

16 25

9 25

12 Плоскость

Общее

уравнение

плоскости

имеет

вид

Ax + By +Cz + D = 0, где

= (A;B;C) называют нормальным вектором плоскости, причем выпол-

няется условие A2 + B2 +C2 ≠ 0 .

Существуют различные способы задания плоскости, выпишем соот-

ветствующие им уравнения:

1. A(x − x

) + B(y − y

) +C(z − z ) = 0

–

уравнение плоскости с извест-

и точкой M0(x0;y0;z0 ), принад-

ным нормальным вектором n

= (A;B;C)

лежащей плоскости.

+ z

=1 – уравнение плоскости в «отрезках», где а, b, с – вели-

чины

отрезков,

отсекаемых

плоскостью

на

осях координат, a ≠ 0,

b ≠ 0, c ≠ 0.

3.	x − x1	y − y1	z − z1	= 0 – уравнение плоскости, проходящей че-
	x − x1	y − y1	z − z1
	x2 − x1	y2 − y1	z2 − z1
	x3 − x1	y3 − y1	z3 − z1

рез три заданные точки Mi (xi ;yi ;zi ), (i =1,2,3) .

Рассмотрим плоскости α: A1x +B1y +C1z +D1 = 0 и β: A2x +B2y +C2z +D2 = 0 .

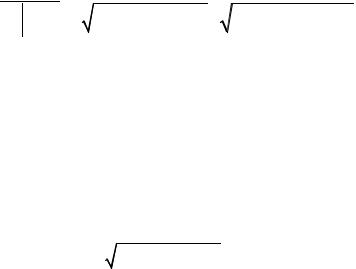
Углом между двумя плоскостями α и β

называется угол между их

нормальными векторами:

A1A2 + B1B2 +C1C2

cosϕ

A 2 + B 2 +C 2

A 2

+ B 2

+C 2

Условие перпендикулярности плоскостей α и β :

n1 n2 = 0 или A1A2 + B1B2 +C1C2 = 0 .

Условие параллельности плоскостей α и β :

= C1

≠ D1 .

Расстояние от точки M1(x1;y1;z1)

до плоскости Ax + By +Cz + D = 0 вы-

числяется по формуле:

d =

| Ax1

+ By1 +Cz1 +

D |

A2 + B2 +C2

Задания для аудиторной работы

184. Построить плоскости, заданные уравнениями:

а) 5x + 2y + 3z −15 = 0;

б) 3x + 2y − 6 = 0 ;

в) 3x −9 = 0;

г) 3x − z = 0.

185. Составить общее уравнение плоскости, которая проходит через:

а) точку C(1; 2; 2) параллельно плоскости xOz;

б) точку M0(3;0;1) и ось Ox;

x − y + z −7 = 0

в) точку M0(1;2;3) перпендикулярно

к плоскостям

3x + 2y −12z + 5 = 0;

г) точку M0(1;1;1) параллельно векторам a1 = (1;2;0), a2 = (0;1;3);

д) начало координат и точки M1(1;0;2), M2(0;0;3);

е) точки M1(1;0;1), M2(0;2;3), M3(0;2;1).

186. Найти угол между плоскостями x − 2y + 2z −3 = 0 и 3x − 4y + 5 = 0 .

187. Вычислить

расстояние

между

параллельными плоскостями

3x + 6y + 2z −15 = 0 и 3x + 6y + 2z +13 = 0 .

188. Составить уравнение плоскости, проходящей через точку M (1;0;2),

перпендикулярно

двум

плоскостям:

2x − y + 3z −1= 0

3x + 6y + 3z −5 = 0 .

189. Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:

а) x − y + 3z +1= 0; 2x − y + 5z − 2 = 0 ;

б) 2x + y + 2z + 4 = 0; 4x + 2y + 4z + 8 = 0;

190. Найти координаты точки Q , симметричной точке P (−3;1;−9) относительно плоскости 4x −3y − z −7 = 0 .

Задания для индивидуальной работы

191. Составить общее уравнение плоскости, которая проходит через: а) точку M (7;−3;5) и параллельна плоскости xOz;

б) точку M (−3;1;− 2) и ось Oz ;

в) точки M1(4;0;− 2), M2 (5;1;7) и параллельна оси Ox ;

г) точку M (2;1;−1) и имеет нормальный вектор n = (1;− 2;3);

д) точку M (3;4;−5) и параллельно векторам a = (3;1;−1), b = (1;− 2;1);

е) точки M1 (3; −1; 4), M2 (5; 2; 6), M3 (2; 3; −3).

192. Составить общее уравнение плоскости, которая проходит через: а) точку А(–3; 1; –2) и ось Ох; б) точку А(–3; 1; –2) и ось Оу;

в) начало координат и точки M(2; 1; 2) и N (1; –2; 3);

г) точку M(2; –3; 5) параллельно плоскости 3x + y − 4z +1= 0.

д) точки M1 (1; 1; 1) и M2 (2;3;4), перпендикулярно плоскости

2x −7y + 5z + 9 = 0;

е) точку M (7;−5;1) и отсекает на осях координат равные положитель-

ные отрезки;

ж) точки А(3; –1; 2) и В(2; 1; ) параллельно вектору a = (5; − 2; −1). 193. Даны точки M1 (3; 0; 4) и M2 (5; 6; 9). Записать уравнение плоскости, проходящей через точку M1 перпендикулярно к вектору M1M2 .

194.Составить уравнение плоскости, которая проходит через две точки M1(1;−1;−2) и M2(3;1;1) перпендикулярно плоскости x − 2y + 3z −5 = 0 .

195.Составить уравнение плоскости, отсекающей на оси Oz отрезок c = −5 и перпендикулярной к вектору n = (−2;1;3).

196.Составить уравнение плоскости, походящей через точку N (2; –1; 1) перпендикулярно к линии пересечения двух плоскостей: 3x − y − z +1= 0

и x + y + 2z +1= 0.

197. Найти косинусы углов между двумя плоскостями:

а) 2x + y − 2z + 6 = 0 ; 2x − 2y + z + 8 = 0 ;

б) 2x − 2y + z + 2 = 0 ; x + y + z −5 = 0;

в) x − 2y + 2z −3 = 0; 3x − 4y + 5 = 0 .

198. Выяснить, при каком значении k следующие пары уравнений будут определять перпендикулярные плоскости:

а) 3x −5y + kz −3 = 0; x + 3y + 2z + 5 = 0 ;

б) 7x − 2y − z = 0; kx + y −3z −1= 0;

в) x − 4y + z −1= 0; 2x + ky +10z −3 = 0 .

199. Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:

а) 3x + 2y − z + 2 = 0 ; 6x + 4y − 2z +1= 0;

б) x −3z + 2 = 0; 2x − 6z −7 = 0 ;

в) 3x + y −5z −12 = 0; 2x + 6z −3 = 0;

г) 2x −3y + z + 8 = 0 ; 4x − 6y −3z −7 = 0 ; д) 5x + 2y −3z −5 = 0; 10x + 4y − 6z + 5 = 0 ; е) 3x + 7y + z + 4 = 0; 9x + 21y + 3z +12 = 0 .

200. Найти расстояние между параллельными плоскостями:

а) x − 2y − 2z + 7 = 0 ; 2x − 4y − 4z +17 = 0 ; б) 6x + 2y − 4z +15 = 0 ; 9x + 3y − 6z +10 = 0 ; в) 3x − 6y + 2z + 35 = 0; 3x − 6y + 2z −7 = 0 .

201.Вычислить объем куба, две грани которого лежат в плоскостях

4x −3y −12z −10 = 0 и 4x + 3y −12z + 3 = 0 .

202.Составить уравнения плоскостей, делящих пополам двугранные углы, гранями которых служат плоскости:

а) 3x − y + 7z − 4 = 0 ; 5x + 3y −5z + 2 = 0; б) 2x − y + 5z + 3 = 0 ; 2x −10y + 4z − 2 = 0 ; в) 5x − 2y + 5z −3 = 0; 2x + y −7z + 2 = 0 .

Ответы.185. а) y = 2; б) y = 0 ; в) 2x + 3y + z −11= 0 ; г) 2x + y − 2 = 0 .

189. а) пересек.;б) совп. 194. 4x − y − 2z −9 = 0 . 195. −2x + y + 3z +15 = 0 .

197. а) 0; б) 3 13 . 200. а) 21 ; б) 2 25126 .

13 Прямая в пространстве. Прямая и плоскость

Существуют различные способы задания прямой в пространстве, выпишем соответствующие им уравнения:

1.A1x + B1y +C1z + D1 = 0, – общие уравнения прямой в пространстве:

A2x + B2y +C2z + D2 = 0

прямая в пространстве определяется как линия пересечения двух плоскостей.

2.	x − x0	=	y − y0	= z − z0	– канонические уравнения прямой в про-
	m		n
				p

странстве с направляющим вектором s = (m,n,p) и точкой (x0,y0,z0 ) , лежащей на прямой.

x = x0 + mt,

+ nt,

– параметрические уравнения прямой в пространстве,

y = y0

z = z

+ pt,

где s = (m,n,p)

– направляющий вектор, t – параметр.

x − x1

y − y1

z − z1

– уравнения прямой в пространстве, про-

− x

− y

− z

ходящей через две заданные точки M1(x1,y1,z1) и M2(x2,y2,z2 ). Пусть две прямые заданы каноническими уравнениями:

L :	x − x1	=	y − y1	= z − z1	; L :	x − x2	=	y − y2	= z − z2 .


1	m1		n1	p1	2	m2		n2	p2

Тогда величина угла между ними определяется как величина угла между

их направляющими векторами и может быть найдена по формуле:

m m + n n

+ p p

cosϕ = cos(s ,s

) =

1 2

m 2 + n 2

+ p 2 m

2 + n 2

+ p

Условие параллельности прямых L

и L

Условие перпендикулярности прямых L1

и L2 : m1m2 + n1n2 + p1p2 = 0 .

Угол

между

прямой

L :

x − x0

y − y0

= z − z0

плоскостью

α : Ax + By +Cz + D = 0 определяется по формуле:

sinϕ =

| Am + Bn +Cp |

A2 + B2 +C2

m2 + n2 + p2

Условие параллельности прямой L и плоскости α : Am + Bn +Cp = 0 .

Условие перпендикулярности прямой L и плоскости α :

= B

= C .

Расстояние от точки M

до прямой

L :

x − x0

y − y0

= z − z0

находят

по формуле: d =

M0M1 ×s |

, где s = (m,n,p) .

| s |

Расстояние между скрещивающимися прямыми

L :

x − x1

y − y1

= z − z1

и L :

x − x2

y − y2

= z − z2

можно найти по

формуле: d =

(M1M2, s1, s2 )

, где M = (x ,y ,z ),M

; y

; z ).

| s1 ×s2 |

Рассмотрим в пространстве плоскость α : Ax + By +Cz + D = 0 и пря-

x = x0 + mt;

мую L , заданную параметрическими уравнениями L : y = y0 + nt;

z = z0 + pt.

Чтобы определить взаимное расположение плоскости α и прямой L ,

рассмотрим уравнение:	A(x0 + mt )+ B (y0 + nt )+C (z0 + pt )+ D = 0.
Отсюда:
t (Am + Bn +Cp)= −(Ax0 + By0 +Cz0 + D).		(4)

1. Если Am + Bn +Cp ≠ 0, то уравнение (4) имеет единственное решение, а, значит, прямая пересекает плоскость в одной точке. При этом,

t =	−(Ax0	+ By0 +Cx0	+ D)	и	координаты	точки	пересечения
	Am + Bn +Cp

(x0 + mt; y0 + nt; z0 + pt ).
2. Если		Am + Bn +Cp = 0 и			Ax0 + By0 +Cz0 + D = 0, то		уравнение (4)

имеет бесконечно много решений, а следовательно, прямая лежит в плоскости.

3. Если Am + Bn +Cp = 0 и Ax0 + By0 +Cz0 + D ≠ 0 , то уравнение (4) не имеет решений, а значит, прямая параллельна плоскости.

Задания для аудиторной работы

203. Составить канонические уравнения прямой, проходящей через: а) точку M0(2;0;3) параллельно вектору a = (3;− 2;− 2);

б) точку A(1;2;3) параллельно оси Ox;

в) точки M1(1;2;3) и M2(4;4;5) .

204. Привести к каноническому виду общее уравнение прямой

x − 2y + 3z − 4 = 0;3x + 2y −5z − 4 = 0.

205. Составить канонические уравнения прямой, проходящей через точ-

ку M1(2;3;−5)	3x − y + 2z + 2 = 0;
	параллельно прямой	+ 3y − 2z + 3 = 0.
	x

206. Установить взаимное расположение двух прямых:

а)

б)

x − 2	=	y	= z +1
4
	3		−2

2x −3z + 2 = 0;

2y − z − 6 = 0

x = 5 −8t;

иy = 4 − 6t;z = 3 + 4t;

x −12z + 49 = 0;

и4y −37z +148 = 0.

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
01.03.2016706.61 Кб148Контрольная работа №1 по высшей математике.pdf
#
01.03.2016720.84 Кб81Контрольная работа №2 по высшей математике.pdf
#
01.03.2016944.4 Кб81Контрольная работа №3 по высшей математике.pdf
#
01.03.2016900.21 Кб88Кр № 4 по математике (ФЗО техн).pdf
#
01.03.201612.6 Mб81математика.doc
#
01.03.2016566.31 Кб253Методичка по математике.1 курс.1 семестр.ФЭИС.pdf