Оптика. Курс лекций. Саечников В А Хомич М И

преобразуем подынтегральное выражение в (1.81) и приравняем его подынтегральному выражению в (1.79). Получим

Обратим внимание на то, что непериодический процесс (в отличие от периодического) имеет сплошной спектр. Это следует из того, что спектральные характеристики процесса a() и b() или f () и () , определяемые формулами (1.80) и

(1.84) являются непрерывными функциями частоты. График спектральной амплитуды f () имеет вид непрерывной кривой (рис. 2.3). Таким образом, непериодиче-

ская функция это суперпозиция гармоник, частоты которых изменяются непрерывно.

Итак, по виду спектра можно судить о характере самого процесса. Например, из того, что спектр солнечного света сплошной (цвета плавно переходят один в другой, между ними нет промежутков), можно сделать вывод, что излучение Солнца непериодический процесс.

Из формул (1.80), определяющих квадратурные компоненты a() и b() , видно, что a() четная функция частоты, а b() нечетная:

где функции a() и b() определены формулами (1.80).

В (1.86) мы впервые ввели отрицательные частоты, что позволило получить более симметричную запись преобразований Фурье, где все интегралы берутся теперь в бесконечных пределах. Подчеркнем, что отрицательные частоты введены формально математически. Содержание этого понятия полностью исчерпывается формулами

(1.87)

Никакого иного смысла термин "отрицательные частоты" не несет. Разумеется, на самом деле (физически) отрицательных частот не существует, так же как нет отрицательных периодов гармонических колебаний. Отрицательные частоты введены математически для удобства. Фактически они фигурируют только на промежуточных этапах расчетов, а в окончательные формулы для измеряемых физических величин никогда не входят.

43

Комплексная запись

Пользуясь формулой (1.83), перепишем (1.86) в виде

Обратим внимание на то, что действительная часть этого комплексного выражения является четной функцией частоты , в то время как мнимая часть нечетной. Поэтому, интегрируя правую и левую части выражения (2.23) по частоте в бесконечных пределах, получаем

Для упрощения записи опустим индекс "к" у комплексной спектральной амплитуды, тогда интегралы Фурье приобретают вид

Если f(t) – четная функция времени, то ее спектральная амплитуда является действительной и четной функцией частоты, а преобразование Фурье может быть записано в виде интеграла от действительной функции по положительным частотам:

44

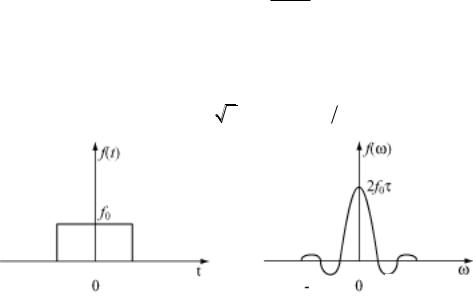
Примеры

Р и с. 2.4

Связь между длительностью импульса и шириной спектра

Указанная закономерность имеет общий характер и выражает одно из основных свойств преобразования Фурье. Нетрудно обосновать это соотношение, исходя из формулы (2.29) для спектральной амплитуды. На рис. 2.5 изображены график функ-

т.е. спектральная амплитуда на нулевой частоте есть постоянная величина, определяемая площадью импульса. Если частота ω увеличивается, то, как видно из (2.29), спектральная амплитуда f ( ) уменьшается. Убывание f ( ) происходит медленно

до тех пор пока период функции cos t , равный 2 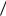, значительно превышает дли-

тельность импульса t , т.е. в области частот, определяемой неравенством T 2 / t.

45

Если же

T t,

то, как видно из рис. 2.5, спектральная амплитуда стремится к нулю. Итак,

Р и с. 2.5

ла (2.36) из приближенной превращается в точную, если использовать интегральные определения длительности импульса и ширины спектра:

В этом случае соотношение (2.36) есть прямое следствие формул (2.28), причем оно справедливо независимо от конкретного вида функции f(t).

Полная и неполная спектральная информация. Спектральная плотность

является комплексной функцией частоты:

ствительную фазу этого колебания. Таким образом, комплексность спектральной амплитуды связана с тем, что разные гармоники, образующие в совокупности процесс f(t), имеют, вообще говоря, различные фазы. Часто такая полная спектральная информация об оптическом процессе бывает не нужна. Более того, в оптике ее трудно экспериментально получить. Поэтому на практике обычно используют более грубую спектральную характеристику процессов — спектральную плотность. По определению спектральной плотностью называется величина, равная квадрату модуля ком-

46

В этом выражении информация о фазах гармонических колебаний, составляющих процесс f(t), утрачена. Тем не менее, для оптики спектральная плотность является важной характеристикой процессов. Спектральная плотность характеризует распределение энергии света по спектру. Именно эта характеристика света наблюдается и может быть экспериментально измерена в опытах.

Равенство Парсеваля

Докажем одну важную формулу, относящуюся к спектральной плотности, и позволяющую глубже понять ее физический смысл. В теории спектральных разложений эта формула носит название "равенство Парсеваля". Она имеет вид

Напомним, что звездочка обозначает комплексное сопряжение.

Итак, равенство Парсеваля доказано. Применительно к оптике это соотношение имеет простой физический смысл. Если под процессом f(t) понимать напряженность электрического поля световой волны в некоторой фиксированной точке пространства, то величина

оказывается пропорциональной энергии светового импульса, прошедшей через площадку единичной площади в окрестности данной точки. С другой стороны, согласно равенству Парсеваля, та же самая величина (энергия) равна интегралу по всем частотам от спектральной плотности поля S() . Это означает, что спектральная плотность

описывает распределение энергии светового импульса по частотам. В этом состоит физический смысл данной характеристики излучения.

2.2Классическая модель излучателя электромагнитных

волн

До сих пор мы изучали свойства электромагнитных волн в пустом пространстве, основываясь на уравнениях Максвелла с равными нулю источниками (плотность заряда) и j (плотность тока). Такие уравнения без источников описывают распространение волн в пустоте, но не позволяют понять, как возникают

47

электромагнитные волны, что является источником этих волн. Ответы на эти вопросы может дать только квантовая теория. Однако исследование именно этих вопросов и привело к открытию квантовых законов природы. Само понятие "квант" было впервые введено Максом Планком в связи с исследованием излучения нагретых тел. Первоначально электромагнитные волны были получены с помощью так называемого "вибратора Герца". Частота излучения вибратора Герца составляет (107 – 108)Гц. Частота видимого света порядка (1014 – 1015)Гц. Существуют ли вибраторы Герца с такими частотами? Поскольку частота излучения возрастает при

уменьшении размеров вибратора, можно предположить, что элементарный источник света обладает чрезвычайно малыми размерами. Была высказана идея, что таким источником может быть атом или молекула.

Обсуждение физики излучения можно провести на основе классической модели атома как системы заряженных частиц, связанных упругими силами. Достоинство этой модели – простота и наглядность, возможность объяснись излучение света исходя из законов электродинамики макроскопических тел. Многие выводы классической теории находят качественное и даже количественное подтверждение в квантовой теории излучения. Классическая модель атома позволяет дать теорию целого ряда явлений, возникающих при взаимодействии света с веществом: поглощение и дисперсия света, разнообразные нелинейные процессы (генерация оптических гармоник, самофокусировка света и т.д.).

Классический образ атома – пара разноименных зарядов, связанных между собой упругой силой. Как могла бы выглядеть такая система? Согласно модели, предложенной Дж. Томсоном, атом представляет собой непрерывно распределенный в некотором объеме положительный заряд, внутри которого находился электрон, удерживаемый в положении равновесия упругой электростатической силой. Будучи выведенным из положения равновесия, электрон совершает гармонические колебания, частота которых 0 определяется зарядом и массой электрона, а также размером атома. Конкретный пример системы подобного типа (для атома водорода) показан на рис. 2.6,а. Здесь точечный отрицательно заряженный электрон находится внутри однородного положительно заряженного шара. На рис. 2.6,б. показана аналогичная модель, которая в большей степени соответствует современным представлениям о строении атома. В этой модели точечное положительно заряженное атомное ядро окружено "электронным облаком", которое в простейшем случае имеет вид однородно заряженного шара.

Ри с. 2.6

Вобеих моделях при смещении центра распределенного заряда относительно точечного заряда противоположного знака возникает кулоновская возвращающая

48

сила F = kx, пропорциональная величине смещения x.Т.о., заряды взаимодействуют подобно шарикам, связанным пружинкой (рис. 2,в).

Как известно из механики, в этом случае ускоренное движение заряда описывается уравнением гармонического осциллятора

силовой постоянной k. Нетрудно вычислить эту постоянную для случая, когда распределенный заряд представляет собой однородно заряженный шар с радиусом a0

Полагая q = 1,6 10–19 Кл, m = 9,1 10–31 кг, a0 = 0,5 10–10 м, получим 0 = 4,5 1016 с–1 ,

или в герцах 0 = 7,2 1015 Гц. Таким образом, частота атомного осциллятора в модели Томсона, вычисленная исходя из известных параметров атома (заряд, масса электрона, размер атома), оказывается близкой к частоте оптических колебаний.

Излучение диполя

Имея в виду классическую модель атома, рассмотрим излучение пары электрических зарядов +q и –q, связанных между собой упругой силой. Такую систему будем называть диполем. Основной характеристикой диполя является дипольный момент,

векторы зарядов. Причем осцилляции дипольного момента обусловлены изменением расстояния между зарядами по гармоническому закону.

Строгое решение задачи об излучении диполя может быть получено путем решения уравнений Максвелла с учетом переменного тока, вызванного ускоренным движением зарядов. В курсе электродинамики показано, что это решение имеет вид

49

над буквой обозначает дифференцирование по времени. Решение (1.112) справедливо для так называемой дальней зоны, т.е. области пространства, находящейся от диполя на расстоянии много больше размера диполя и длины волны излучения.

Поле излучения диполя представляет собой сферическую волну и имеет структуру, представленную на рис. 2.7.

электромагнитной волны в каждой точке связана с напряженностью E электрического поля в этой же точке тем же соотношением, что и для плоской волны.

Гармонические колебания диполя

Вычислим энергетические характеристики излучения диполя, считая, что диполь совершает гармонические колебания с амплитудой A и с частотой 0:

x0 – единичный вектор, направленный вдоль линии, соединяющей заряды (рис. 2.7). Используя формулы (1.112) и (1.113), получим

Формулы (1.114), (1.115) показывают, что излучение диполя линейно поляризо-

Учитывая формулы (1.114), (1.115), можно записать

50

(1.116) по времени, получаем интенсивность излучения диполя на расстоянии r

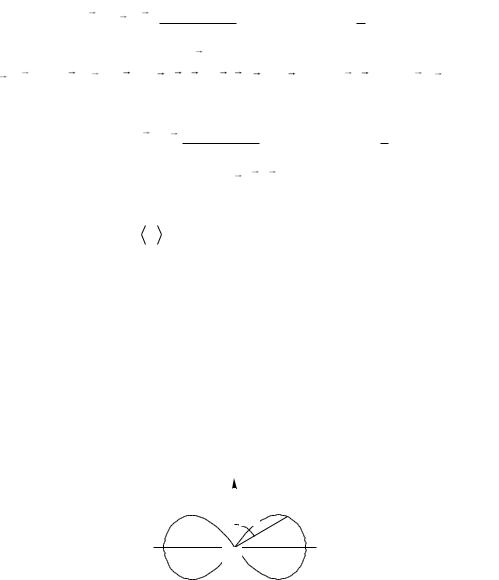
Зависимость интенсивности от направления выражается в (1.117) множителем sin2 . Максимальная интенсивность наблюдается при = /2, т.е. в экваториальной плоскости: максимум интенсивности соответствует направлению, перпендикулярному оси диполя. Вдоль оси диполя ( = 0) энергия не излучается. Угловое распределение излучаемой осциллирующим диполем энергии показано на рис. 2.8. с помощью "диаграммы направленности". Длина отрезка, проведенного из начала координат до пересечения с линией r = sin2 , пропорциональна интенсивности распространяющейся в данном направлении волны. Распределение интенсивности по направлениям в пространстве характеризуется поверхностью, которая получается вращением кривой на рис. 2.8 вокруг оси OX.

0O

Р и с. 2.8 Полную энергию, излучаемую диполем за 1 с по всем направлениям

(мощность излучения) можно найти, вычисляя <S> через поверхность сферы радиусом r с центром в начале координат. Разобьем сферу на кольца координатными поверхностями = const и + d = const. Площадь такого кольца равна 2 r2sin d , а значение <S> во всех его точках можно считать одинаковым. Поэтому полная излучаемая мощность

Согласно формуле (1.118), излучаемая осциллятором мощность пропорциональна квадрату амплитуды его дипольного момента и четвертой степени частоты (обратно пропорциональна четвертой степени длины волны). Этот закон играет большую роль

51

в теории рассеяния света. Короткие волны рассеиваются сильнее чем длинные. Этим объясняется голубой цвет неба и красный цвет Солнца на закате.

Выражаемый формулой (1.118) поток излучения осциллятора через поверхность сферы не зависит от ее радиуса, т.е. через любую охватывающую осциллятор замкнутую поверхность протекает за 1 с одинаковая энергия. Этот факт объясняет

Радиационное затухание

Осциллятор совершает незатухающие колебания лишь в том случае, когда эти колебания поддерживаются каким-либо внешним источником. Без такого источника колебания будут затухать даже при движении в абсолютно пустом пространстве, так как осциллятор теряет энергию на излучение. Затухание колебаний атомного осциллятора, связанное с потерей энергии на излучение, получило название радиационного затухания. Затухание колебаний можно описать, вводя в уравнение

Надо помнить, однако, что никаких сил сопротивления, никакой "вязкости" в обычном смысле этого слова здесь нет. Используя полученное выше выражение (1.118) для излучаемой осциллятором мощности, можно сделать оценку времени жизни атома в возбужденном состоянии.

пропорциональна квадрату амплитуды. Излучаемая осциллятором мощность Pизл, представляющая собой скорость уменьшения энергии (–dW/dt) в соответствии с (1.118) также пропорциональна квадрату амплитуды. Выражая A2 через энергию W из (1.119) и подставляя в правую часть (1.118), получаем, что скорость уменьшения энергии осциллятора пропорциональна его энергии:

Из уравнения (1.120) следует, что энергия возбуждения осциллятора уменьшается вследствие потерь на излучение по экспоненциальному закону:

Здесь э = 1/2 – время радиационного затухания, в течение которого энергия осциллятора уменьшаемся в e = 2,72 раз. Амплитуда A колебаний осциллятора также убывает экспоненциально:

52