
Komyak_A_I_Molekulyarnaya_spektroskopia
.pdf
потенциальной энергии в поворотных точках классического движения. Часто, когда говорят о полной энергии осциллятора, имеют в виду его кривую потенциальной энергии.
Итак, двухатомная молекула как классический осциллятор колеблется
с одной частотой |
1 |
|
|
k |
|
|
–1 |
|
|
|
k |
|
~ |
1 |
|
|
k |
|
|
–1 |
|
|
|
|
|
|
[с |
|
], |
|
|
|
[рад/с] или |
|
|
|
|
|
[см |
|
], |
||
2 |
|
|
|
|
|
|
|
2 c |
|
|
|
|
|||||||||
определяемой квазиупругой постоянной k.
При процессах поглощения или испускания света такая система будет поглощать или испускать одну частоту. Таким образом, спектр классического осциллятора будет характеризоваться этой одной частотой, определяемой квазиупругой постоянной k и приведенной массой .
3.2.2.Квантовомеханический случай
Вквантовой механике колебания двух ядер в двухатомной молекуле рассматриваются как в классической физике – движение двух масс m1 и
m2 заменяется перемещением одной частицы массой |
m1m2 |
|
и |
m m |
|
||
1 |
2 |
|
|
смещаемой из положения равновесия на величину q0. Для нахождения полной колебательной энергии E такой частицы необходимо решить уравнение Шрѐдингера типа
|
|
, |
|
H E |
(3.13) |
||
|
|
|
|
где – волновая функция гармонического осциллятора, а H –
оператор энергии, соответствующий классическому выражению Н(р, q) функции Гамильтона от обобщенных импульсов (р) и обобщенных координат (q)
|
|
|
|
|
|
H p, q T |
p V q |
1 |
|
p2 |
1 kq2 . |
(3.14) |
||||||||||||||
|
|
|
|
|
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Заменив |
|
классическое |
выражение |
импульса |
р его |
оператором pˆ |
||||||||||||||||||||
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
pˆ |
|
|
|
|
|
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 i q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
1 |
kq2 |
h |
2 |
|
|
|
2 |
|
|
|
1 |
kq2 . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
H |
pˆ |
|
|
|
|
|
|
|
|
|
(3.15) |
|||||||||
|
|
|
|
|
|
2 |
2 |
8 q2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
93
Собственные значения энергии E и собственные функции этого
оператора находим путем решения уравнения вида (3.13) записанного для конкретной рассматриваемой системы
|
h2 |
. |
2 |
|
|
1 |
kq2 |
|
q E |
(q) |
|
|
|||||
|
|
|
|
|
|||||||||||||
|
|
8 2 q2 |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (q) |
|
|
8 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(Е |
|
V ) (q) 0 . |
|
(3.16) |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
q2 |
|
|
|
|
h2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При определенных ограничениях, налагаемых на функцию |
|
(она |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
должна быть однозначной, непрерывной, исчезающей на бесконечности и иметь интегрируемый квадрат модуля), уравнение (3.16) имеет решения при значениях E полной энергии:
|
|
1 |
|
|
|
E h |
|
|
, |
(3.17) |
|
2 |
|||||
|
|
|
|
где – классическая частота колебаний, определяемая формулой
|
1 |
|
|
k |
|
[с–1], |
(3.18) |
2 |
|
|
|
||||
|
|
|
|
|
|
а – колебательное квантовое число, принимающие целые значения 0, 1, 2, ... Если выражать полную энергию E в см–1, то равенство (3.17) можно записать, опуская h, т. е.
~ |
|
1 |
|
|
|
E |
|
|
, |
(3.19) |
|
2 |
|||||
|
|
|
|
где ~ – волновое число (частота колебаний, выраженная в см ).
–1
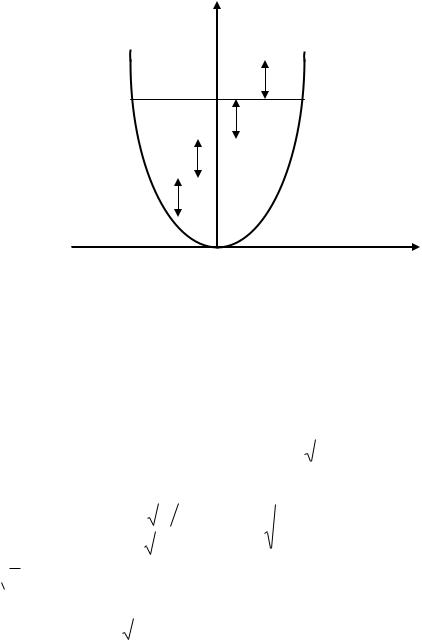
Формула (3.17) дает равностоящие невырожденные уровни энергии (см. рис. 3.5). Согласно правилу отбора для гармонического осциллятора разрешены все переходы с изменением колебательного квантового числа на единицу, т. е. 1. Таким образом, в спектре ИК-поглощения и испускания могут комбинировать между собой только соседние энергетические уровни, разность энергий которых определяется формулой:
E +1 – E = h , |
(3.20) |
а частота соответствующего перехода между этими уровнями равна
94
|
E 1 E |
[c–1] |
|
|
|
h |
|
|
|||
|
|
|
|
|
|
или |
|
|
|
|
|
~ |
|
–1 |
]. |
(3.21) |
|
E 1 E |
[cм |
||||
|
|
|
~ |
|
|
|
|
|
k . |
||
и совпадает с частотой классического осциллятора 1 2 c |
|||||
Итак, квантовомеханический осциллятор обладает дискретным равноотстоящим набором значений энергии. Классический осциллятор, наоборот, обладает непрерывным набором значений энергии, зависящим от амплитуды колебаний. Далее. Если минимальное значение энергии классического осциллятора равно нулю, то минимальная энергия гармонического осциллятора в квантовой механике отлична от нуля и равна
E0 |
|
h |
[Дж] |
|
||
|
|
|||||
|
|
|
2 |
|
|
|
или |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
E0 |
|
|
[cм–1], |
(3.22) |
||
2 |
||||||
|
|
|
|
|
||
т. е. молекула в основном колебательном состоянии |
0 обладает |
|||||
определенной нулевой энергией. Это значение энергии не так уж мало,
~
особенно для легких молекул типа Н2 (частота колебаний молекулы Н2 равна 4401 см–1), и его необходимо учитывать при расчете некоторых термодинамических постоянных на основе данных ИК-спектров.
95
V(q)
4  E4
E4
E3
3
|
2 |
|
|
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
E1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|
E0 |
|
|||
|
0 |
|
|
|
q |
||||
|
|
|
|
||||||
Рис. 3.5. Уровни энергии и переходы между ними гармонического осциллятора в
квантовой механике
Рассмотрим соответствие между классическим и квантовомеханическим осцилляторами. Для этого проанализируем выражения для собственных волновых функций квантовомеханического осциллятора, которые в общем виде записываются следующим образом:
|
|
|
q |
2 |
|
|
|
q , |
|
|
|
|
|
|
|
|
|||
|
N |
2 |
H |
|
|
(3.23) |
|||
|
|
|
|
|
|
|
|
|
где N – нормировочный множитель, равный
|
|
|
|
|
|
|
|
|
4 2 |
|
4 |
, |
2 |
k |
|
, |
|||||
|
|
|
|
|
|
|
||||
|
2 ! |
h |
h |
|||||||
|
|
|
|
|
||||||
а H 
 q ) – полином Чебышева Эрмита степени относительно q. Первые четыре полинома Чебышева – Эрмита равны следующим
q ) – полином Чебышева Эрмита степени относительно q. Первые четыре полинома Чебышева – Эрмита равны следующим
|
|
|
|
выражениям при x |
q : |
|
|
Н0 (х) = 1, H1 ( х) = 2х, Н2(х) = 4 х2 – 2, |
|||
|
|
|
Н3 (х) = 8х3 – 12х. |
|
|
|
q 2 |
Наличие множителя |
2 в функции (3.23) приводит к быстрому ее |
||
спаду (уменьшению за пределами области классического движения).
Число узлов функции (3.23) |
равно числу нулей полиномов Чебышева- |
|||
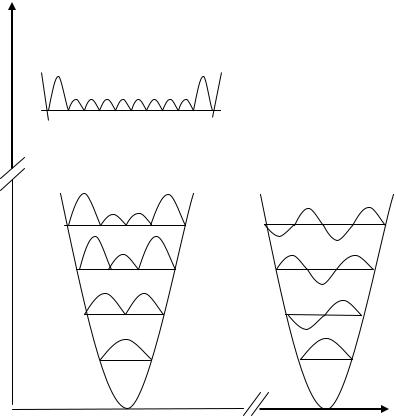
Эрмита, равных . Вид волновых функций |
|
для малых , а также их |
||
|
|
|
|
|
квадратов 2 |
(или * ) |
приведены на |
рис. 3.6. Каждый график |
|
|
|
|
|
|
|
|
96 |
|
|
построен на прямой, изображающей соответствующий уровень энергии.
Слева на |
этом |
рисунке показана зависимость |
квадрата |
волновой |
|||
функции ( 2 ) от |
|
|
|
||||
|
q , определяющего вероятность различных значений |
||||||
|
|
|
|
|
|
|
|
координаты. |
В |
случае нулевого колебательного |
состояния ( 0 ) |
||||
функция |
2 |
с точностью до нормирующего множителя |
выражается |
||||
|
|
|
|
|
|
|
|
2q 4
формулой 4 , т. е. представляет собой функцию ошибок Гаусса. Она имеет максимум при q = 0. Для возбужденных состояний ( = 1, 2, ….), получается ряд максимумов, причем наибольшая вероятность колебательной координаты получается вблизи поворотных точек классического движения. Чем больше , тем ближе общий характер квантовомеханического распределения вероятности как функции колебательной координаты к соответствующему распределению, получающемуся на основе классической теории. Отличие состоит в том, что в квантовой механике за пределами классического движения вероятность нахождения системы отлична от нуля, хотя и быстро убывает при изменении q.
97
V(r) а
=10
б
|
=3 |
|
|
=2 |
|
|
=1 |
|
|
=0 |
|
0 |
0 |
q |
|
Рис. 3.6. Графики волновых функций и
а– их квадратов модулей;
б– квантового осциллятора для небольших
Это связано с различием подходов к рассмотрению колебательного движения в квантовой и классической механике.
3.3. КОЛЕБАНИЯ ДВУХАТОМНОЙ МОЛЕКУЛЫ КАК АНГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
3.3.1. Аппроксимация зависимости потенциальной энергии от межьядерного расстояния в реальной молекуле (кривая Морзе)
Силы взаимодействия между атомами в реальной двухатомной молекуле сложным образом зависят от изменения равновесного расстояния q r re Пропорциональность силы от величины смещения
q справедлива только для очень малых смещений из положения равновесия или для колебаний с бесконечно малой амплитудой. Если для
o
сравнительно легких молекул расстояние между атомами равно 1 (0,1
98

нм), то признак малости амплитуды будет хорошо выполняться при
колебаниях с |
амплитудой |
q0 = 0,1 |
o |
(0,01 нм). В этом случае |
|||
|
|||||||
потенциальная |
энергия |
двухатомной |
молекулы |
выражается |
|||
квадратичной |
функцией |
следующего |
вида |
V 1 2kq2 |
и |
||
удовлетворительно описывающей колебания вблизи положения равновесия. Реальные колебания молекулы всегда ангармоничны. Ангармонизм выражен тем сильнее, чем больше амплитуда колебаний. А при сравнительно больших амплитудах колебаний, примерно 0,05 ÷ 0,07 нм, достигается предел прочности связей в молекуле, и она распадается на составляющие атомы или ионы. В случае больших амплитуд нужно рассматривать не параболическую потенциальную кривую (рис. 3.4) V(q), а истинную кривую, изображенную на рис. 3.2. Хорошим приближением для описания истинной кривой потенциальной энергии двухатомной молекулы является функция Морзе, удовлетворительно описывающая экспериментальные кривые зависимости V(q) для сравнительно легких молекул. Общее выражение функции Морзе имеет вид
V q D |
e |
1 r re 2 |
, |
(3.24) |
|
|
|
|
где De – энергия диссоциации молекулы, отсчитываемая от минимума потенциальной кривой, – постоянная величина для данной молекулы, характеризующая формулу кривой, а r – re = q – смещение атомов из положения равновесия.
Рассмотрим несколько положений колеблющейся молекулы.
1. Пусть q = r – re стремится к большой величине, а в пределе – к бесконечности (q ). Тогда мы видим, что V(q) будет стремиться к De , т. е. V(q) = De , что соответствует асимптотическому приближению
правой ветви (рис. 3.2) к нулю (к энергии диссоциации молекулы).
2. Пусть q изменяется незначительно. При малых смещениях q из
положения равновесия функцию q можно разложить в |
ряд |
вида |
1 q 1 2 2q2 ... Ограничившись двумя членами ряда |
(так |
как |
последующие члены имееют порядок малости больше двух и ими можно пренебречь), можно записать выражение (3.24) в виде:
V q D |
1 1 q 2 D 2q2 . |
(3.25) |
e |
e |
|
Анализируя (3.25) видим, что потенциальная энергия вблизи положения равновесия выражается квадратичной функцией от q , т. е. приходим к выводу, что молекула ведет себя как гармонический
99
осциллятор. Если сравнить полученное выражение с равенством (3.8), то можно видеть, что k =2 De 2 , т. е. коэффициент упругой силы пропорционален энергии связи De . С другой стороны, зная квазиупругую постоянную k и энергию связи De , можно найти :
|
k |
|
2De . |
(3.26) |
Квазиупругую постоянную молекулы обычно находят из частот колебаний:
~ |
|
1 |
|
|
|
|
k |
|
|
|
|
|||
e |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
2 c |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~2 |
|
2 |
c |
2 |
. |
|
|
(3.27) |
|||||
k e 4 |
|
|
|
|
|
|||||||||
Подставив это выражение в формулу (3.26), получим |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
2 c e |
|
|
|
|
|
|
|
|
, |
(3.28) |
||||
|
|
|
|
|
2De |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
где – приведенная масса молекулы. |
|
Таким образом, постоянную |
||||||||||||
можно находить из спектроскопических измерений. |
|
|||||||||||||
3. Пусть, при сближении ядер в молекуле q = r – re |
есть величина |
|||||||||||||
отрицательная (так как r меньше re и сравнительно велика по
абсолютному значению). Тогда второе слагаемое в формуле (3.24) велико и V(q), будет возрастать. Этот случай хорошо передает ход кривой потенциальной энергии в левой ее части (см. рис. 3.2).
3.3.2 Уровни энергии, правила отбора и спектры двухатомной молекулы как ангармонического осциллятора
Потенциальная кривая гармонического осциллятора представляет собой симметричную параболу (см. рис. 3.4). Действительные потенциальные кривые двухатомных молекул асимметричны (см. рис. 3.2). Около минимума они близки к параболе, затем расширяются более быстро, чем парабола, и одна из их ветвей (правая) приближается к конечному пределу. Это приводит к тому, что расстояния между последовательными колебательными уровнями энергии не остаются постоянными, как для гармонического осциллятора, а постепенно уменьшаются (рис. 3.7). Колебательные уровни сближаются и сходятся по мере приближения к границе диссоциации.
100
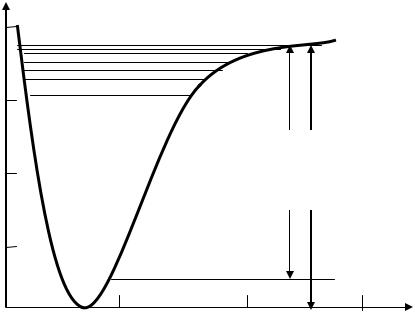
На рис. 3.7 приведены колебательные уровни молекулы Н2. Аналогичное схождение испытывают и уровни энергии других молекул.
~ 10–3 , cм–1
400
300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
D0 |
De |
||
|
|
|
4 |
|
|
|
|
|||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
=0 |
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
0,1 |
|
0,2 |
0,3 |
r, нм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.7. Зависимость потенциальной энергии молекулы водорода от расстояния между ядрами и (ось ординат смещена вниз)
Сближение колебательных уровней с приближением к границе диссоциации связано с тем свойством уровней, что они располагаются тем теснее, чем шире потенциальная кривая. Для потенциальной кривой, имеющей форму параболы, мы имели равноотстоящие уровни энергии (см. рис. 3.5), причем расстояние между уровнями будет тем меньше, чем шире парабола. Для кривой, расширяющейся кверху быстрее параболы, уровни энергии будут постепенно сближаться ввиду того, что правая часть кривой Морзе приближается к конечному пределу, т. е. ширина кривой стремится к бесконечности при конечном значении энергии, происходит сгущение колебательных уровней энергии вблизи границы диссоциации. За границей диссоциации мы имеем непрерывную совокупность уровней энергии.
Следует отметить, что закон приближения кривой к пределу существен, так как от его характера зависит, получается ли вблизи границы бесконечное или конечное число колебательных уровней. Для молекулы Н2 на рис. 3.7 число колебательных уровней конечно, получается всего лишь 15 уровней ( = 0, 1, …, 14). За уровнем = 14 следует граница диссоциации.
101

Расположение колебательных уровней энергии двухатомной молекулы как ангармонического осциллятора мы можем получить, если в уравнение Шрѐдингера (3.16) вместо потенциальной функции гармонического осциллятора подставим функцию Морзе. Решение уравнения Шрѐдингера типа (3.16) с этой функцией дает следующее значение для колебательной энергии:
E h 1 2 h x 1 2 2 , |
( 3.29) |
где х – константа ангармоничности, по порядку величины равная 10 2 10 3 . Эта формула наряду с основным членом, пропорциональным1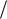 2 , содержит и поправочный член, пропорциональный ( 1
2 , содержит и поправочный член, пропорциональный ( 1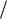 2)2 и
2)2 и
обусловленный ангармоничностью колебаний.
Если энергию, как и волновые числа, измерять в см–1, то формулу (3.29) можно переписать, опустив постоянную Планка h:
~ |
~ |
2 |
(3.30) |
E 1 2 x 1 2 . |
|||
Как видно из выражения (3.30) , уровни энергии ангармонического осциллятора уже не являются равноотстоящими. Расстояние между соседними уровнями уменьшается с увеличением до нуля, т. е. уровни энергии сходятся к некоторому пределу – границе диссоциации.
Чтобы получить спектр ангармонического осциллятора, необходимо знать населенность колебательных уровней энергии, вероятности переходов между ними и правила отбора.
Населенность уровней энергии подчиняется больцмановскому распределению
|
|
|
|
E |
|
|
n |
|
n g |
kT |
, |
(3.31) |
|
|
0 i |
|
|
|
|
а так как gi = 1 для колебательных уровней энергии, то последняя формула (3.31) перепишется следующим образом:
|
|
n |
E |
|
|
n |
|
kT |
, |
(3.32) |
|
|
0 |
|
|
|
Здесь n – число частиц на колебательном уровне, характеризуемом колебательным квантовым числом , п0 – число молекул на нулевом уровне энергии, k – постоянная Больцмана, а Т – температура среды. Не анализируя вероятности переходов (они определяются степенью перекрытия колебательных волновых функций) между колебательными уровнями энергии, приведем правила отбора для колебательного квантового числа . Возможны переходы в ИК поглощении и
102
