
principdalambera
.pdf
При неподвижной точке A имеет место сферическое движение. Связав жестко с телом подвижную систему отсчета, можно записать:
KA = I A ω,
где I A – тензор инерции тела относительно точки A.
По формуле Бура (см. сложное движение точки), имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d K A |
= |
d K A |
+ω × |
|
A , |
|||||
|
|
|
|
K |
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
d t |
|
d t |
e |
|||||||
|
|
|
|
|
|
|
|
|||||||
d |
K |
A |
– относительная производная кинетического момента в подвижной |
|||||||||||
d t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
системе отсчета, жестко связанной с телом. В этой системе I A = const , значит
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d K |
A |
= I A |
d ω |
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
d t |
|
|
||||||||
но |
|
|
|
|
|
|
|
|
|
|
|
d ω |
= |
d ω |
= ε, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
d t |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
|
|
|
|
||||||
поскольку |
d ω |
= |
d ω |
+ω ×ω, |
|
а ω ×ω= 0, так как ω = ω . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
d t |
|
d t |
e |
|
|
|
|
|
|
e |
|
|
e |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Теперь |
d K |
A |
= I A ε +ω×(I A ω). |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
d t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ΦA = −I A ε −ω×(I A ω) |
(3.2) |
|||||||||||||||
|
|
|
|
|
|
|
|
L |
||||||||||||||||||||
при неподвижной точке A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Φ |
= −I |
|
|
ε −ω×(I |
|
ω), |
(3.3) |
|||||||||||
|
|
|
|
|
|
|
|
L |
C |
C |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
если С – центр масс, поскольку движение относительно центра масс сферическое.
10
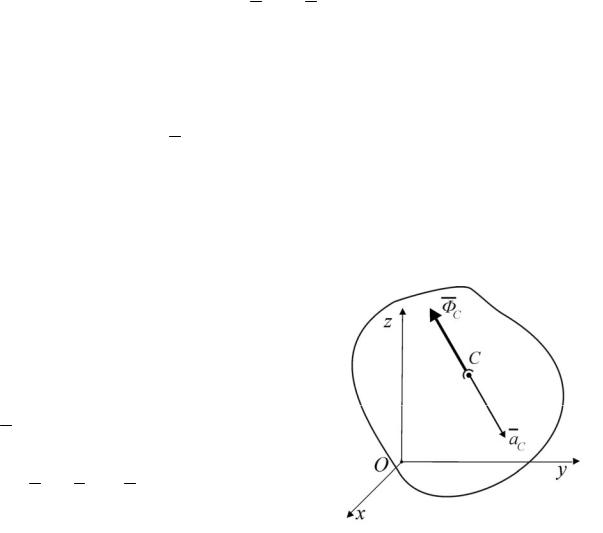
4. ПРИВЕДЕНИЕ СИЛ ИНЕРЦИИ ЧАСТИЦ ТВЕРДОГО ТЕЛА К ЦЕНТРУ
Любая система сил приведением к выбранному центру A может быть замена результирующей силой, равной главному вектору сил системы и результирующей парой, равной главному моменту сил системы относительно центра приведения.
Точно также можно привести к центру A и силы инерции частиц твердого
тела: |
|
{dΦ |
} (Φ |
A ,mΦA ), |
|
|||||||
|
|
(4.1) |
||||||||||
где |
|
|
|
|
|
|
|
|
Φ = −M a , |
(4.2) |
||
|
Φ |
A |
= U |
|||||||||
|
|
|
|
|
|
|
|
A |
C |
|
||
– главный вектор сил инерции частиц твердого тела, |
|
|||||||||||
а |
|
ΦA = |
|
ФA = −I Aε −ω×(I A ω). |
(4.3) |
|||||||
m |
L |
|||||||||||
– главный момент сил инерции частиц твердого тела, если точка A неподвижная или является центром масс, (см. формулы 3.1 – 3.3).
Частные случаи приведения сил инерции к центру
а) Поступательное движение
За точку приведения берется центр масс тела. Вращение тела относительно центра масс отсутствует, следовательно mCΦ = 0 .
Итак:
{dΦ} ΦC ; ΦC = −M aC .
Рис 4.1
11

б) Сферическое движение твердого тела
В этом случае за центр приведения удобно взять неподвижную точку O . Свяжем с телом подвижную систе-
|
|
|
|
|
|
|
|
|
|
му отсчета Oxyz . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Теперь: {dΦ |
} (ΦΟ ,mOΦ ), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
где ΦO = - M aC , aC – ускорение цен- |
||||||||
|
|
|
|
|
|
|
|
|
|
тра масс; |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
m |
Φ = −I |
O |
ε −ω×(I |
O |
ω). |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
||
|
|
|
|
Рис 4.2 |
|
|
|
|
в) Общий случай движение твер- |
|||||||||
|
|
|
|
|
|
|
|
|
|
дого тела |
|
|
|
|
|
|||
|
|
В общем случае движения твердого тела, если за центр приведения взять |
||||||||||||||||
центр масс, то получаем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
{dΦ |
} (ΦC ,mCΦ ), |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ε −ω×(I |
|
|
ΦC = −M aC , |
|
|
|
|
|
||||||||
m |
Ф = −I |
C |
C |
ω). |
|
|
|
|
|
|||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
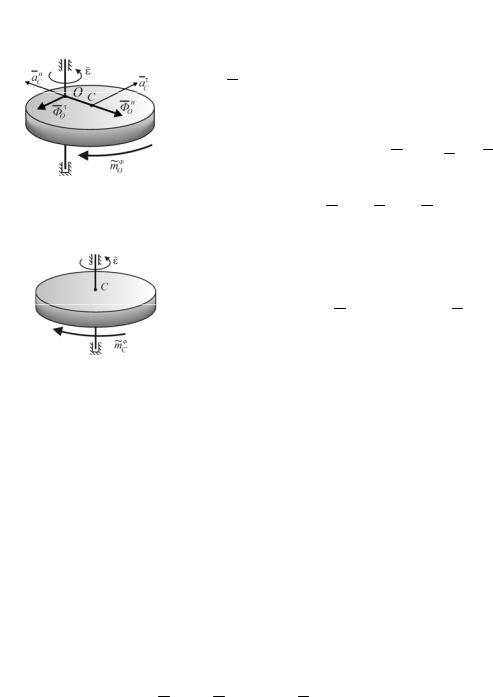
г) Вращение тела вокруг неподвижной оси |
|
|
|
|
|
|||||||||||||
|
|
Это |
частичный |
случай сферического |
|
|
|
|
|
|||||||||
движения тела. За центр приведения возьмем |
|
|
|
|
|
|||||||||||||
точку O на оси вращения. Так как ускорение |
|
|
|
|
|
|||||||||||||
центра масс ac перпендикулярно оси враще-
ния, то результирующая сила инерции ΦO лежит в плоскости
Ускорение центра масс равно
aC = aCn+ aCτ ,
Рис. 4.3
12
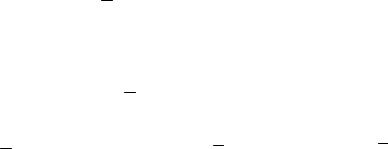
где an = ω2 h, aτ = εh. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
c |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Результирующая сила инерции найдется по формуле: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
τ |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
′ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ΦO =ΦO |
+ΦO |
, причем ΦO |
|
O1C , ΦO |
O C . |
|||||||||||||||||||||||||||||
В данном случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ω= ω |
|
|
; ε = ε |
|
; ω= |
|
0 |
|
|
; ε = |
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|||||||||||||||||||||||||
|
|
|
k |
k |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
ε |
|
||||||
|
|
|
|
|
|
|
Jx |
−Jxy |
|
−Jxz |
|
|
|
0 |
|
|
|
|
−Jxz ε |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Теперь I0 ε = |
−J yx |
J y |
|
−J yz |
|
|
0 |
|
|
= |
−J yz ε |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
−Jzx |
−Jzy |
|
Jz |
|
|
|
|
ε |
|
|
|
|
Jz ε |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично получаем
|
−Jxz ω |
, ω×(I0 ω)= |
|
|
i |
|
|
|
|
|
|
j |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||||||
I0 ω= |
−J yz ω |
0 |
|
0 |
|
|
|
|
ω |
= |
|
ω2 J yz − |
|
ω2 Jxz . |
||||||||||||||||||
|
|
i |
j |
|||||||||||||||||||||||||||||
|
Jz ω |
|
|
|
|
|
|
|
- Jxz ω J yz ω Jz ω |
|
|
|
|
|
||||||||||||||||||
Или, в матричной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
ω×(I0 ω)= |
|
ω2 J yz |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
−ω2 Jxz |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
−ω2 J yz +εJxz |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В итоге |
|
m |
Φ = |
|
ω2 J |
xz |
+εJ |
yz |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
−Jz ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n +Φ |
|
|
n |
= −M a n |
|
|
τ |
= −M a τ, |
|||||||||||||||||||
|
Φ |
= Φ |
, Φ |
, Φ |
||||||||||||||||||||||||||||
|
|
|
Ο |
Ο Ο |
|
Ο |
|
|
|
|
|
|
c |
|
|
|
O |
|
|
|
c |
|||||||||||
m0Φ = τ(εJxz −ω2 J yz )+ j (εJ yz +ω2 Jxz )−k ε Jz .
13
Частные случаи вращения тела
1. Если тело вращается вокруг главной, нецентральной оси, то
Jxz = J yz = 0 .
m0Φ можем рассмотреть как алгебраическую величну:
{dΦ} (mOΦ ,ΦO ),
ΦO =ΦOn +ΦOτ ,mOΦ = −εJz .
2. Если тело вращается вокруг главной, центральной оси, то
ΦC = 0, {dΦ} (mOΦ ).
д) Плоское движение
Рассмотрим движение тела параллельно плоскости его материальной симметрии. За центр приведения возьмем центр масс.
Относительное движение – вращение вокруг главной центральной оси тела zc . Кинетический момент относи-
тельно этой оси можно рассматриваешь как величину алгебраическую
|
|
|
|
|
|
Φ |
|
dKz |
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
K |
z |
= J |
z |
ω, m |
= − |
|
= −J |
z |
ε. |
|
|
||||||||||
|
|
|
|
C |
|
d t |
|
|
|||
|
|
|
C |
|
C |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 4.6 |
|
Итак |
|
|
|
|
|
|
|
|
|
|
{dΦ |
} (ΦC ,mCΦ ),ΦC = −M aC , mCΦ = −JzC ε. |
|
|
|||||||
14
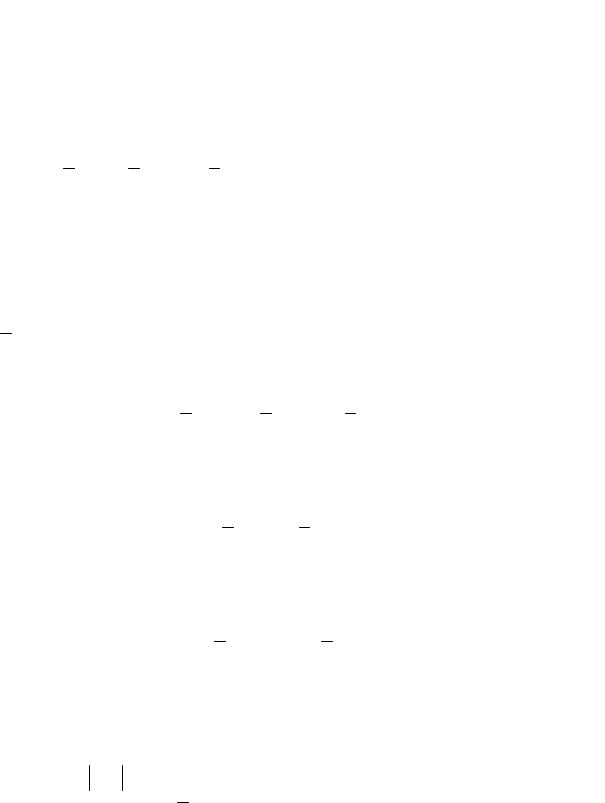
5 Определение динамических реакций опор.
При движении несвободного твёрдого тела принято реакции связей представлять в виде суммы двух составляющих – статической и динамической.
В общем случае по принципу Даламбера имеем
({Rk }n ; {Fke}n ,{dΦ}n ) 0 ,
где { |
|
k } |
|
– система сил реакций связей; |
|
|
R |
n |
|
||||
{Fke} |
|
|
|
|||
– система внешних заданных сил, дейст- |
|
|||||
|
|
n |
|
|
Рис. 5.1 |
|
вующих на точки механической системы; |
||||||
{dΦ |
}n – система инерции точек механической системы. |
|
||||
Если представить, что
{Rk }n ({Rk ст}n +{Rk дин}n ),
то статическими составляющими будем называть те, которые зависят только от внешних заданных сил:
({Rk ст}n ,{Fke}m ) 0 .
Динамическими составляющими сил реакций связей будем называть те, которые зависят от движения тела и определяются силами инерции тела
({Rk дин}m ,{dΦ }) 0 .
В частности, для тела вращающегося тела в подшипнике вокруг неподвижной оси и закреплённого в подшипнике B и подпятнике A на этой оси будем иметь
Примем AB =h.
2)Заданные силы {Fk }n .
3)Связи: подшипник B , подпятник A.
15

Их реакции: X B ,YB ,X A ,YA ,ZA .
4)Введём в рассмотрение силы инерции тела
{dΦ} (ΦA ,LΦA ) (ΦA , LΦA ),
ΦA (ΦAx ,ΦAy ); ΦA = −MaC .
LΦ = ε I - ω2 I ;
Φ A x zx zy LAZ = −εIz ; LΦA y = ε Izy +ω2 Izx .
5) В соответствии с принципом Даламбера
({Fke}m ,X A ,YA ,ZA ,X B ,YB ,{dΦ}) 0 .
6) Составим уравнения равновесия для нахождения динамических составляющих реакций опор в соответствии с зависимостью
({Rдин},{d Φ}) 0;
∑Fx = X Aдин + X Bдин +ΦAx = 0 ;
∑Fy =YAдин +YBдин +ΦAx = 0 ;
∑Fz = ZAдин = 0 ;
∑mx F = −YBдин h +εJzx −ω2 Jzy = 0 ;
∑my F = X Bдин h +εJzy +ω2 Jzx = 0 .
Таким образом, для нахождения динамической составляющей будем иметь систему уравнений. Из этих уравнений видно, что при быстром вращении тела динамические составляющие могут достигать больших величин. Динамические составляющие обращаются в нуль, если ΦA = 0, Jzy = Jzx = 0 т.е. ось враще-
ния будет главной центральной осью инерции тела. Итак: Если ось вращения тела является главной центральной осью инерции тела, то реакции подшипников этой оси при движении не отличаются от статических. В этом случае говорят,
16
что ось вращения – свободная ось, а тело уравновешенно. В противном случае тело неуравновешенно.
Виды неуравновешенности
1. Ось вращения центральная, |
|
но не главная. Т.е. для плоского дис- |
|
ка ось вращения проходит через его |
|
центр, но не перпендикулярно плос- |
|
кости диска. Говорят, что тело стати- |
|
чески уравновешенно, но динамиче- |
|
ски неуравновешенно. Динамическое |
|
воздействие вращающегося тела |
|
приводится к паре сил, (Φ'' , Φ' ) ко- |
Рис. 5.2 |
торая уравновешивается ди намиче- |
|
скими составляющими реакций |
|
(RA ,RB ), RA = −RB
m(RA ,RB )= h RB = h yB2 + xB2 = (Jzx2 + Jzy2 )(ε2 +ωx ).
|
|
|
Такую неуравновешенность можно уп- |
|
|
|
||||||||||
ростить только путём динамической баланси- |
|
|
|
|||||||||||||
ровки на специальных стендах. |
|
|
|
|
|
|
||||||||||
|
|
|
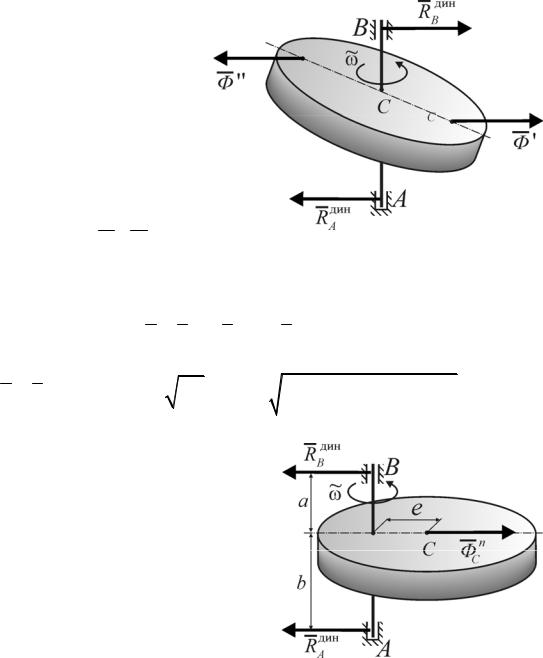
2. Ось вращения главная, но не цен- |
|
|
|
||||||||||
тральная. Т.е. для диска ось вращения пер- |
|
|
|
|||||||||||||
пендикулярна плоскости диска, но не прохо- |
|
|
|
|||||||||||||
дит через его центр. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Здесь динамическое воздействие вра- |
|
|
|
||||||||||
щающегося |
тела |
сводится |
к |
силе |
|
|
|
|||||||||
Φ |
c |
= M a = M ω2e (для |
|
ω=const ). |
Если |
|
|
Рис. 5.3 |
||||||||
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
||
a и в |
расстояние от диска до подшипников, |
|
|
|
||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дин |
|
|
в |
|
|
2 |
|
дин |
|
a |
2 |
|
|
|
|
R |
|
= |
|
|
|
M |
ω e; |
R |
|
= |
|
M ω e. |
|
|
|
|
|
а |
+в |
|
a +в |
||||||||
|
|
|
|
|
A |
|
|
|
B |
|
|
|||||
17
Динамические составляющие представляют собой параллельные силы. Такая неуравновешенность над статической неуравновешенностью. Её можно устранить путём статической балансировки.
В общем случае вращающееся неуравновешенное тело не уравновешенно ни статически, ни динамически. Силы инерции можно в общем случае привести к двум скрещивающимся силам и, соответственно, силы реакции – две скрещивающиеся силы. Устранить такую неуравновешенность можно с помощью статической и динамической балансировки.
Балансировка машин
Несбалансированный ротор вращающейся машины является источником переменных сил, действующих на элементы машины, в частности на ее подшипниковые опоры, и значительно сокращает ресурс машины. Процесс уменьшения этих сил носит название балансировки.
Балансировка осуществляется при помощи установки на вращающихся частях машины дополнительных (балансировочных) масс для создания инерционных сил, равных по величине и противоположных по направлению силам, вызванным несбалансированностью. При этом нет необходимости (да и возможности) устанавливать такие массы в каждом сечении ротора. Обычно предполагается, что ротор является твердым телом (так называемый жесткий ротор). В этом случае для компенсации влияния всех дисбалансов в нем достаточно двух балансировочных масс, установленных в разных сечениях ротора. Если машина состоит из нескольких жестких роторов, связанных между собой относительно гибкими валами, все вышесказанное относится к каждому из роторов.
Балансировка роторов машин обычно осуществляется при помощи специальных балансировочных станков. Однако при сборке ротора из отбалансированных частей, установке его в собственные опоры и стыковке его с остальными вращающимися частями машины возникают дополнительные источники дисбаланса. Они определяются:
•наличием технологических допусков при сборке ротора;
•точностью посадки ротора в его подшипниковые опоры;
•точностью центровки сопряженных валов;
•влиянием на величину дисбаланса условий эксплуатации (влияние перекачиваемой жидкости для насосов, температурные условия при эксплуатации), которые невозможно воспроизвести при балансировке на станке.
18

Кроме того, в процессе эксплуатации машины происходит увеличение дисбаланса. Это связано с появлением сколов или налипанием среды на вращающиеся части машины, их коррозионным износом, ослаблением связей в составных роторах, ослаблением опор и фундаментных конструкций. При этом работоспособность машины может сохраняться, и ремонт ее не требуется.
Корректировка масс ротора осуществляется либо путем добавления материала в «легкой» части ротора, либо путем его удаления в «тяжелой».
В условиях производства балансировка проводится на универсальных или специальных балансировочных станках. Для серийного и массового производства выпускаются высокопроизводительные автоматические балансировочные линии. Балансировочные станки различаются по частоте вращения ротора, по точности измерения дисбаланса, по способу измерения и виду индикации, по виду привода ротора во вращательное движение, по габаритам и массе роторов, по способу корректировки масс.
Некоторые из балансировочных станков для автомобильных колес приведены на рисунке.
19
