
Метод Гаусса-Жордана_методичка
.doc(0.1)
(0.2)
(0.3)
(1.1)
(1.2)
(1.3)
Таблица I(1) с первым столбцом свободных членов соответствует системе уравнений, эквивалентной системе (9), а с вторым столбцом свободных членов - системе уравнений, эквивалентной системе (10). Для системы (9) последнее уравнение имеет вид
0 x1 + 0 x2 + 0 x3 + 0 x4 = 1,
что показывает несовместность системы (9).
Для системы (10) последнее уравнение имеет вид
0 x1 + 0 x2 + 0 x3 + 0 x4 = 0.
Отсюда следует, что его можно отбросить, и что система (10) эквивалентна системе из 2 – х уравнений с 4 – мя неизвестными, представляемой строками (1.1), (1.2) и вторым столбцом свободных членов в таблице I(1). Мы можем продолжать решать систему (10), используя следующую таблицу I(1)
|
I(1) |
1 |
-3/2 |
3/2 |
5/2 |
-1/2 |
|
|
0 |
17 |
-13 |
-3 |
7 |
(1.2)
или
|
|
x1 |
x2 |
x3 |
x4 |
b |
|
I(0) |
2 |
-3 |
3 |
5 |
-1 |
|
|
3 |
4 |
-2 |
6 |
2 |
|
|
-4 |
6 |
-6 |
-10 |
2 |
|
I(1) |
1 |
-3/2 |
3/2 |
5/2 |
-1/2 |
|
|
0 |
17 |
-13 |
-3 |
7 |
(0.1)
(0.2)
(0.3)
(1.1)
(1.2)
В таблице I(1) можно выбрать в качестве ведущего любой ненулевой элемент, стоящий во второй строке и в любом, кроме первого, столбце. Выберем в качестве ведущего в таблице I(1) элемент (-3), стоящий на пересечении 4 - ого столбца и 2 – ой строки. Тогда ведущая строка – вторая, ведущий столбец- четвертый.
Итерация 2. Преобразуем таблицу I(1) в новую таблицу I(2), в которой четвертый столбец (ведущий) будет единичным. Для этого преобразуем первую строку таблицы I(1) так, чтобы вместо 5/2 стоял 0. Для этого нужно из строки (1.1) вычесть (поэлементно) ведущую строку (1.2), умноженную на (-5/6). Получим
|
1 |
38/3 |
-28/3 |
0 |
16/3 |
Все элементы ведущей строки (1.2) делим на ведущий элемент (т.е. в нашем конкретном случае - на число (-3)) и полученную новую строку записываем на ее место (т.е. на место (2.2)) в таблице I(2).
Таблица I(2) будет иметь вид (две последние строки, выделенные курсивом)
|
|
x1 |
x2 |
x3 |
x4 |
b |
|
I(0) |
2 |
-3 |
3 |
5 |
-1 |
|
|
3 |
4 |
-2 |
6 |
2 |
|
|
-4 |
6 |
-6 |
-10 |
2 |
|
I(1) |
1 |
-3/2 |
3/2 |
5/2 |
-1/2 |
|
|
0 |
17 |
-13 |
-3 |
7 |
|
I(2) |
1 |
38/3 |
-28/3 |
0 |
16/3 |
|
|
0 |
-17/3 |
13/3 |
1 |
-7/3 |
(0.1)
(0.2)
(0.3)
(1.1)
(1.2)
(2.1)
(2.2)
Обе строки уже были ведущими, поэтому мы не можем в таблице I(2) выбрать ведущий элемент. Переходим к Заключительному этапу.
Заключительный этап. Все строки были ведущими, поэтому система, определяемая таблицей I(2), и, следовательно, система (10) разрешима. При этом переменные x1 и x4 – базисные, а x2 и x3 – свободные. Запишем систему линейных алгебраических уравнений, соответствующую последней таблице I(2).
x1 + (38/3) x2 - (28/3) x3= 16/3
x4 - (17/3) x2 + (13/3) x3 = - 7/3 (11)
Из (11) можно однозначным образом выразить базисные переменные через свободные и правую часть. На свободные переменные при этом нет никаких ограничений, т.е. они могут принимать любые значения. Таким образом, множеством решений системы (11) и, следовательно, системы (10) является следующее множество Xb,
Xb = { x = (x1, x2, x3, x4) : x1 = 16/3 - (38/3) x2 + (28/3) x3, x4 = - 7/3 + (17/3) x2
- (13/3) x3, x2 и x3 – любые.}
Примеры 1 и 2 проиллюстрировали работу метода Гаусса – Жордана и все возможные способы остановки метода. Повторим основные выводы, которые можно сделать из изложенного.
-
Метод остановится через конечное число итераций r. При этом выяснится, является система совместной или несовместной.
-
Если система совместна, то число базисных переменных равно числу итераций r, а число свободных переменных – (n – r). Все базисные переменные однозначно выражаются через свободные переменные и соответствующие свободные члены.
-
Если система совместна и общее решение содержит хотя бы одну свободную переменную, то число решений бесконечно. Если же свободных переменных нет (n = r), то решение единственно.
-
Базисные переменные на каждой итерации можно выбирать различными способами, поэтому запись общего решения может быть разной. Однако, само множество решений одно и то же.
Вернемся к анализу
систем уравнений (1) и (10).
Если в системах (1) и (10)
все соответствующие (с одинаковыми
номерами) коэффициенты при переменных
совпадают, то системы (1) и (10)
называются соответствующими.
Множества решений систем (1) и (10)
обозначаем Xb
и X0.
Система (1) совместна, если Xb
≠
![]() .
.
Теорема 3. Если в однородной системе уравнений (10) n > m, то система (10) имеет бесконечное число решений.
Доказательство.
Однородная система всегда совместна
(набор
![]() =
(
=
(![]() ,
,![]() ,…,
,…,![]() ),
где
),
где
![]() =
0 при всех j
= 1,…,n,
очевидно, является её решением),
т.е. X0
≠
=
0 при всех j
= 1,…,n,
очевидно, является её решением),
т.е. X0
≠
![]() .
Если решать ее методом Гаусса – Жордана,
то он остановится через r
итераций и r
≤ min
(m,n)
= m
< n.
Тогда число свободных переменных есть
n
– r
≥ n
– m
> 0. Отсюда следует, что система имеет
бесконечное число решений. Теорема
доказана.
.
Если решать ее методом Гаусса – Жордана,
то он остановится через r
итераций и r
≤ min
(m,n)
= m
< n.
Тогда число свободных переменных есть
n
– r
≥ n
– m
> 0. Отсюда следует, что система имеет
бесконечное число решений. Теорема
доказана.
Теорема 4.
Пусть y
= (y1,
y2,
… , yn)
и z
= (z1,
z2,
… , zn)
– решения однородной системы (10),
т.е. y
![]() X0,
z
X0,
z
![]() X0.
Тогда
X0.
Тогда
-
x* = y + z = (y1 + z1, y2 + z2, … , yn + zn)
 X0,
X0, -
x
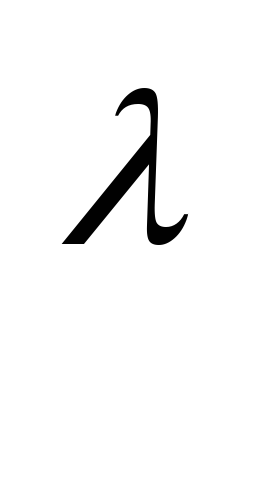 =
=
 y
= (
y
= ( y1,
y1,
 y2,
… ,
y2,
… ,
 yn)
yn)
 X0.
X0.
Доказательство.
1) Так как y
![]() X0,
z
X0,
z
![]() X0,
то
X0,
то
![]() =
0, i
= 1,…,m,
=
0, i
= 1,…,m,
![]() =
0, i
= 1,…,m. (12)
=
0, i
= 1,…,m. (12)
Проверим, является
ли x*
решением (10).
Для этого рассмотрим
![]() .
В силу (12)
.
В силу (12)
![]() =
=
![]() =
=
![]() +
+
![]() = 0, т.е. x*
= 0, т.е. x*
![]() X0.
X0.
2) Так как
![]() =
=
![]()
![]() =
0, то x
=
0, то x
![]() =
=
![]() y
y
![]() X0.
Теорема доказана.
X0.
Теорема доказана.
Рассмотрим теперь
соответствующие
друг другу системы (1) и (10).
Пусть система (1) совместна,
т.е. Xb
≠
![]() .
Пусть
.
Пусть
![]() =
(
=
(![]() ,
,![]() ,…,
,…,![]() )
– некоторое фиксированное
частное
решение системы (1), т.е.
)
– некоторое фиксированное
частное
решение системы (1), т.е.
![]() =
bi
при всех i
= 1,…,m.
=
bi
при всех i
= 1,…,m.
Теорема 5. Пусть
система (1) совместна и
![]() =
(
=
(![]() ,
,![]() ,…,
,…,![]() )
– некоторое её фиксированное
частное
решение. Тогда
)
– некоторое её фиксированное
частное
решение. Тогда
1) произвольное
решение x
= (x1,
x2,
… , xn)
является суммой (почленной) этого
фиксированного решения
![]() и некоторого решения z
= (z1,
z2,
… , zn)
соответствующей однородной системы;
и некоторого решения z
= (z1,
z2,
… , zn)
соответствующей однородной системы;
2) если z
= (z1,
z2,
… , zn)
– произвольное решение однородной
системы (10),
то x
=
![]() + z
= (
+ z
= (![]() + z1,
+ z1,![]() + z2,…,
+ z2,…,![]() + zn)
– решение соответствующей неоднородной
системы (1).
+ zn)
– решение соответствующей неоднородной
системы (1).
Доказательство.
1) Так как
![]()
![]() Xb
и x
Xb
и x
![]() Xb,то
Xb,то
![]() =
bi
,
=
bi
,
![]() =
bi
при всех i
= 1,…,m. (13)
=
bi
при всех i
= 1,…,m. (13)
Построим набор z = (z1, z2, … , zn) следующим образом:
zj
=
![]() - xj,
j = 1, … , n. (14)
- xj,
j = 1, … , n. (14)
Покажем, что z – решение соответствующей однородной системы. Действительно, в силу (14) и затем (13)
![]() =
=
![]() =
=
![]() -
-
![]() =
bi
- bi
= 0.
=
bi
- bi
= 0.
Так как это верно для любого i = 1,…,m, то набор z, определенный в (14), является решением системы (10).
2) Пусть z
= (z1,
z2,
… , zn)
![]() X0,
т.е.
X0,
т.е.
![]() = 0
при всех i
= 1,…,m.
(15)
= 0
при всех i
= 1,…,m.
(15)
Положим
xj
=
![]() + zj,
j = 1, … , n. (16)
+ zj,
j = 1, … , n. (16)
Покажем, что x = (x1, …, xn) – решение системы (1). Из (16), (13) и (15) следует
![]() =
=
![]() =
=
![]() +
+
![]() =
bi
+ 0 = bi
при всех i,
т.е. x
=
bi
+ 0 = bi
при всех i,
т.е. x
![]() Xb.
Теорема доказана.
Xb.
Теорема доказана.
Теорема 5 утверждает, что для того, чтобы найти все решения системы (1), достаточно найти одно её решение и все решения соответствующей однородной системы (10).
Это всё, что мы пока можем сказать о системе из m линейных уравнений с n переменными. Будем возвращаться к анализу таких систем во всех следующих темах.
