1. Метричні простори та приклади

М-ну Х елем. пр-ру дов. природи назив. метричним простором, якщо кожній парістав. у відповідність числотак, що вик. умови:

1. (аксіома тотожності)

2. (акс. симетрії)

3.

Число наз. відст. між елем. х та у, а ф-ціюназ. метрика.

Метричний простір – це пара

Якщо на м-ні Х визначити і, то отримаємо різні метричні простори.

Приклади

1. Х=R

Акс. 1,2,3 виконуються.

2. Елем. пр-ру єn-вимірним вектори.

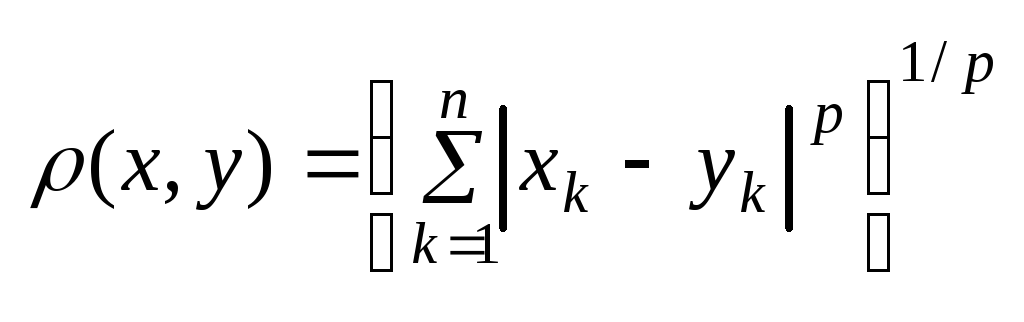
Акс. 1,2,3 виконуються.

Доведемо, що аксіома 3 виконується. Візьмемо довільне

Робимо заміну:

Для р=1 нерівн. виконується.

Розглянемо

Використаємо допоміжну нерівність: нерівність Юнга:

, p,q – спряжені. Числа спряжені, якщо .

Доведемо нерівність Юнга.

Рівн.Юнга очевидно справедливе, коли а=0 і b=0, тому розглянемо

Площа прямокутника зі сторонами a та b не перевищує суму площ S₁ та S₂

Нехай

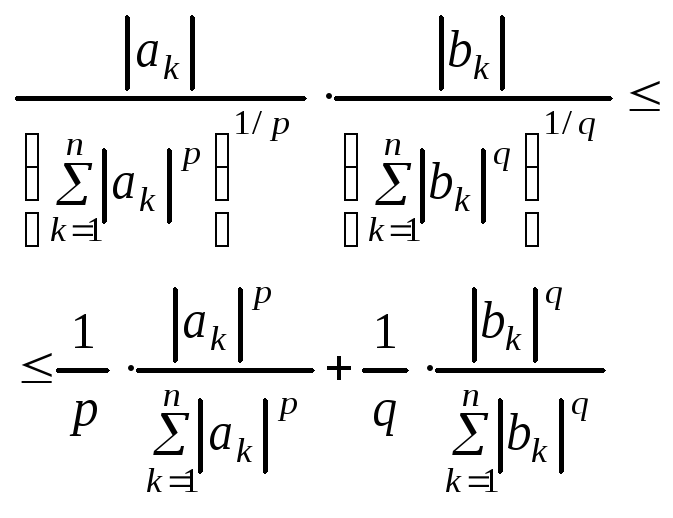
- нерівність Гьольдера.

Заст.цю нерівн. для акс.3

Поділимо обидві частини нерівності на :

це нерівн. справедл. для будь-яких наборів

Нерівність має назву: нерівність Мінковського.

3.

елем.простору є n-вимірним вектори з дійсними коорд.

4.

Елем.простору – послід.дійсних чисел.

- збігаються (1)

- збігаються (2)

- відст. визн. коректно, ряд з озн. метрики збіг. Це випливає з озн. порівн. та збіж.(1) і (2). Справедл. нерівн. три кут. випливає з нерівн. Мінковського для рядів.

5. - простір обмеж. числ. послід.

6.- простір ф-цій неперервних наЕлем. про-ру -- візнач. наі неперервні.

Справедл. акс 1 і 2. Покажемо, що справедл. нерівн. три кут.

2. Відкриті та замкнені множини

Нехай Х – метр. простір.Відкритою кулею з центром у точці х₀ радіуса r називають множину точок таких, що відстань. Позначають цю відкриту кулю:

Замкненою кулею з центром у точці х₀ радіуса r називають множину точок х є Х, таких, що відстань між .

Позначають замкнену кулю:

Геометрія куль залежить від метрики.

Приклад

1. Елементами цього простору є х=(х₁,х₂) та у=(у₁,у₂)

Ставиться задача побудувати кулю

2. Елементами цього простору є х=(х₁,х₂) та у=(у₁,у₂)

Околом т. х_о будемо наз. довільну відер. кулю, яка містить цю точку.

Будемо позначати О(х_о)

Нехай А – множина у метричному просторі Х, . Т. х₀ гранична точка множини А, якщо у будь-якому околі т. х₀ існує нескінчена множина точок множини А.

х₀ – гранична точка множини А, якщо у будь-якому околі т. х₀ міститься хоча б одна точка множини А, яка відрізняється від точки х₀

Приклади

1. Х=R A=N

Граничних точок не існує

2. B=R

Кожна точка множини є граничною.

Множина А називається замкненою, якщо у неї не існує граничних точок, які їй не належать.

Замиканням множини А будемо називати множину А до якої додали всі її граничні точки. Позначаємо . Для замкненої множини А=.

Приклади

Х=R

N-замкнена; = N

Q-незамкнена;

Нехай А- підмножина метр. простору Х, точка х₀, що належить Х називається межовою точкою множини А, якщо у будь-якому околі точки х₀ існують точки, які належать множині А і точки, які множині А не належать.

Приклад

Х=R.

А[a,b] a,b – межові,

B(a,b)

Означення

називається ізольованою, якщо існує окіл точки х₀ в якому немає інших точок множини А.

Приклад

Х=R. A=N. Кожна точка ізольована.

А – підмножина метричного простору Х, називається внутрішньою точкою множини А, якщо

Множина А називається відкритою, якщо кожна її точка внутрішня.

Приклад

Х=R A=N – замкнена, не відкрита

B=Q – незамкнена, не відкрита

Приклади відкритих множин:

Х- м.п. - відкрита множ.

Х=R - відкрита множина

Властивості замикання:

1. Множ. і може збігатися

2.

3.

4.