Пособие по мат. стат

81

2 (n 1)S 2 .

02

Критическая область строится в зависимости от конкурирующей гипотезы.

Первый случай, когда конкурирующая гипотеза имеет вид

H1 : 2 02 .

В этом случае строят правостороннюю критическую область. Критическую точку χкр2 χα;2 k находят по таблице критических точек

распределения 2 (прил. 2), и тогда правосторонняя критическая область определяется неравенством

χ2 χкр2 ,

аобласть принятия нулевой гипотезы неравенством

χ2 χкр2 .

Обозначим значение критерия, вычисленное по данным наблюдений,

и по таблице критических точек распределения 2 , по заданному уровню значимости и числу степеней свободы k n 1, найти критическую точку

χкр2 χα;2 k .

Если χнабл2 χкр2 нет оснований отвергнуть нулевую гипотезу.

Если χнабл2 χкр2 нулевую гипотезу отвергают.

Второй случай, когда конкурирующая гипотеза имеет вид:

H1 : 2 02 .

значимости, k n 1 – это число степеней свободы. Критическая точка также ищется по таблице критических точек распределения 2 . Наблюдаемое значение χнабл2 ищется по той же формуле, что и в первом случае.

Если χнабл2 χкр2 нет оснований отвергнуть нулевую гипотезу.

Если χнабл2 χкр2 нулевую гипотезу отвергают.

Таким образом, во втором случае получаем левостороннюю критическую область.

Третий случай: конкурирующая гипотеза имеет вид

H1 : 2 02 .

В этом случае строят двустороннюю критическую область.

Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу о равенстве неизвестной генеральной дисперсии 2

отвергают.

Гипотеза о неизвестной вероятности «успеха» в испытаниях Бернулли

Основная гипотеза H0 : p p0 , альтернативная гипотеза H1 может быть трех видов: а) p p0 ; б) p p0 ; в) p p0 . Во всех трех случаях для проверки используется статистика критерия

83

где w относительная частота «успехов» в n наблюдениях.

Далее критические точки и области для проверки выбираются так же, как при проверке гипотезы о неизвестном среднем при известной дисперсии.

Замечание. Этим методом можно пользоваться только при больших объемах выборки (порядка сотен).

Пример. Партия изделий принимается, если доля брака составляет не более 2 %. Среди случайно отобранных 500 изделий оказалось 13 бракованных. Следует ли принять партию (на уровне значимости 0,05)?

Решение. Из условия задачи следует, что необходимо проверить гипотезу H0 : p p0 при конкурирующей гипотезе

H1 : p p1 p0 ,

где p0 0,02 (2 %). Относительная частота брака составляет

образом, партию изделий можно принять.

Описанные выше критерии проверки гипотез можно представить в виде табл. 4.1.

Проверка гипотез для двух выборок

Пусть имеются две независимые выборки x1, x2,..., xn и y1, y2,..., ym , имеющие нормальное распределение с параметрами ax , x и ay , y

соответственно. Обычно строится задача проверки их однородности, т.е. равенства обоих параметров, либо необходимо проверить равенство параметров по отдельности.

84

Гипотеза о равенстве дисперсий двух выборок

На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, методов измерений и т.д.

Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам объемов n1 и n2 , извлеченным из этих

совокупностей, найдены исправленные выборочные дисперсии Sx2 и S y2 .

Требуется по исправленным дисперсиям, при заданном уровне значимости, проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой, т.е.:

H0 : σ2x σ2y .

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий, примем отношение большей исправленной дисперсии к меньшей, т.е. случайную величину:

S 2

F б .

Sм2

Эта величина, при условии справедливости нулевой гипотезы, имеет распределение Фишера со степенями свободы k1 n1 1, k2 n2 1, где n1 объем выборки, по которой вычислена большая исправленная дисперсия, n2 объем выборки, по которой вычислена меньшая дисперсия.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай. Конкурирующая гипотеза имеет вид

H1 :σ2x σ2y.

В этом случае строят одностороннюю, а именно правостороннюю, критическую область. Обозначим отношение большей исправленной дисперсии к меньшей, вычисленное по данным выборок, через Fнабл .

Получим следующее правило проверки нулевой гипотезы: для того, чтобы, при заданном уровне значимости, проверить нулевую гипотезу H0 :σ2x =σ2y

при конкурирующей гипотезе H1 :σ2x σ2y , надо вычислить

S 2

Fнабл б (3.5)

Sм2

85

Таблица 4.1 Алгоритм проверки гипотез о значениях параметров нормального распределения и вероятности успеха

86

и по таблице критических точек распределения Фишера (прил. 4), по заданному уровню значимости и числам степеней свободы k1 и k2 , найти критическую точку Fкр Fα; k1; k2 .

Если Fнабл Fкр нет оснований отвергнуть нулевую гипотезу.

Если Fнабл Fкр нулевую гипотезу отвергают.

Пример 1.

По двум независимым выборкам объемов n1 12, n2 15 , извлеченным из нормальных генеральных совокупностей X и Y , найдены исправленные

0,05 проверить нулевую гипотезу

H0 :σ2x =σ2y

о равенстве генеральных дисперсий, при конкурирующей гипотезе

H1 :σ2x σ2y.

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

11,41 Fнабл 6,52 1,75.

Как было отмечено выше, при данной конкурирующей гипотезе мы получаем правостороннюю критическую область.

По таблице критических точек распределения Фишера, по уровню

В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в

87

предположении справедливости нулевой гипотезы, была равна принятому уровню значимости .

Обозначим отношение большей исправленной дисперсии к меньшей, вычисленное по данным выборок, через Fнабл . Получим следующее правило

проверки нулевой гипотезы: для того, чтобы, при заданном уровне значимости, проверить нулевую гипотезу H0 :σ2x =σ2y при конкурирующей

гипотезе H1 :σ2x σ2y , надо вычислить

S 2

Fнабл б

Sм2

и по таблице критических точек распределения Фишера, по уровню значимости 2 и числам степеней свободы k1 и k2 , найти критическую точку

Fкр Fα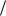2; k1; k2 .

Если Fнабл Fкр нет оснований отвергнуть нулевую гипотезу.

Если Fнабл Fкр нулевую гипотезу отвергают.

Пример 2

По двум независимым выборкам объемов n1 10, n2 18, извлеченным из генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии Sx2 1, 23 и Sy2 0, 41. При уровне значимости 0,1 проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей

гипотезе H1 :σ2x σ2y .

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

Fнабл 1,230,41 3.

По таблице критических точек распределения Фишера, по уровню значимости, вдвое меньшим заданного, т.е. при 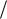2 0,05 , и числам

степеней свободы k1 10 1 9, k2 18 1 17 , находим критическую точку

Fкр F0,05;9;17 2,5.

Так как Fнабл Fкр , нулевую гипотезу о равенстве генеральных

дисперсий отвергаем. Другими словами, выборочные исправленные дисперсии различаются значимо. Например, если бы рассматриваемые дисперсии характеризовали точность двух методов измерений, то следует предпочесть тот метод, который имеет меньшую дисперсию (0,41).

88

Гипотеза о равенстве средних при известных дисперсиях

Пусть генеральные совокупности X и Y распределены нормально, причем их дисперсии известны. По независимым выборкам объемов n и m ,

извлеченным из этих совокупностей, найдены выборочные средние x, y .

Требуется по выборочным средним, при заданном уровне значимости, проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е.

H0 :ax ay .

В качестве критерия проверки нулевой гипотезы принимают

Полученный критерий – нормированная нормальная величина, т.е. случайная величина Z имеет стандартное нормальное распределение: M (Z ) 0 , при справедливости нулевой гипотезы, (Z ) 1, так как выборки

независимы.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай, когда конкурирующая гипотеза имеет вид

89

H1 :ax ay .

В этом случае строят двустороннюю критическую область. Для проверки нулевой гипотезы о равенстве генеральных средних при известных дисперсиях надо вычислить наблюдаемое значение критерия

Если Zнабл zкр нет оснований отвергнуть нулевую гипотезу.

Если Zнабл zкр нулевую гипотезу отвергают. Второй случай. Конкурирующая гипотеза имеет вид

H1 :ax ay .

В этом случае строят правостороннюю критическую область. Для этого надо вычислить наблюдаемое значение критерия Zнабл по формуле (3.6) и по

таблице функции Лапласа найти критическую точку из равенства

0,1 zкр 1 22α .

Если Zнабл zкр нет оснований отвергнуть нулевую гипотезу. Если Zнабл zкр нулевую гипотезу отвергают.

Третий случай, когда конкурирующая гипотеза имеет вид:

H1 :ax ay .

В этом случае строят левостороннюю критическую область. При конкурирующей гипотезе такого вида надо вычислить наблюдаемое значение Zнабл и по таблице функции Лапласа найти критическую точку по равенству

0,1 zкр 1 22α .

90

Если Zнабл zкр , тогда нет оснований отвергнуть нулевую гипотезу. Если Zнабл zкр , тогда нулевую гипотезу отвергают.

извлеченным из нормальных генеральных совокупностей, найдены выборочные средние x 1250, y 1275 . Генеральные дисперсии известны:

Критическая область двусторонняя. Найдем правую критическую точку по равенству

извлеченным из нормальных генеральных совокупностей, найдены

гипотезу H0 :ax ay при конкурирующей гипотезе H1 :ax ay .

Решение. Подставив данные задачи в формулу (3.6), получим