Решения задач ЕГЭ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Кавказский федеральный университет

Предмет:

Физика

Файл:

тенциальная энергия будет равна:

.pdf

Скачиваний:

1393

Добавлен:

10.06.2015

Размер:

5.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2311 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Решение

1. Напряжённость поля от заданного
заряда, расположенного в центре сфер:
E	0	= k	q	= 62,5 В :
			R2
				м
2. Поскольку заряд сфер сосредоточен
на их поверхности, то сферы, проводящие и
их можно рассматривать как соответст-
вующие точечные заряды, расположенные
в центре.
3. У проводящей сферы напряжённость					Рис. 260. Заряженные сферы
поля при r ≤ R равна нулю, поэтому внеш-

няя сфера при дальнейшем рассмотрении может не учитываться.

4. В соответствии с принципом суперпозиции электрических полей резуль-

тирующая напряжённость в точке А определится в виде:

= E

− E

= k

− k

2E0

−

=10

;

(2,5R)2

6,25

261. Проводящий шар радиусом r = 5 см с зарядом q = 4 нКл окружён сферической оболочкой из диэлектрика радиусом R = 10 см с диэлектрической проницаемостью вещества ε = 2. Найти напряжённости поля на внутренней (1) и внешней (2) поверхностей диэлектрика.

Решение

1. Напряжённость поля в точке 1, на поверх-

ности заряженной сферы (точка лежит в диэлек-

трической среде):

k q

9 109 4 10−9

= 7,2

кВ

;

2 25 10−4

2. Напряжённость поля в точке 2:

k q

109

4 10−9

=1,8

кВ

;

Рис. 261. Диэлектрический

ε R2

0,01

шаровой слой

262. Конденсатор, заряженный до напряжения U1 = 200 В, соединяют разноимёнными обкладками с конденсатором такой же ёмкости, но заряженным до напряжения U2 = 400 В. Определить установившееся напряжение батареи.

Решение

U = U	2	− U ;	U	0	= U	= U2 − U1 =100 В;
	2	1		0	2	2
					2	2

263. Конденсатор, электрическая ёмкость которого С1 = 5 мкФ, заряжен так, что разность потенциалов между его пластинами U1 = 80 В. Второй конденсатор, электрическая ёмкость которого С2 = 10 мкФ, имеет разность потенциалов между пластинами U2 = 50 В. Разноимённо заряженные пластины попарно соединяют. Чему станет равен модуль разности потенциалов?

101

											Решение
1.	Заряды конденсаторов до соединения:
									Q1 = C1U1; Q2 = C2U2 ;
2.	Заряд батареи после соединения клемм разноимёнными полюсами:
								Q 0 = Q 1 − Q 2 = C U 1 − C 2 U 2 ;
3.	Электрическая ёмкость параллельно соединённых конденсаторов:
									C0 = C1 + C2 ;
4.	В соответствии с законом сохранения заряда:
	C	U	0	= C	U	2	− C U ;		U	0	= C2U2 − C1U1	= 10 50 −5 80 6,67 B;
	0		0	2		2	1	1		0	C1 + C2	15
											C1 + C2	15

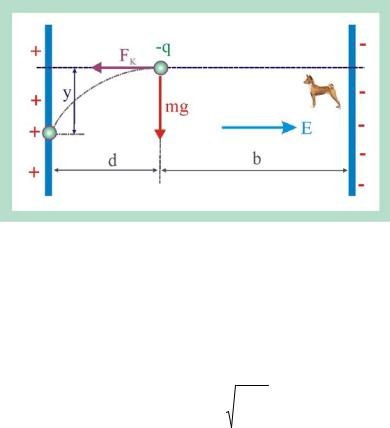
264. Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряжённостью Е = 2 105 В/м, направленное слева направо. Между пластинами помещён шарик на расстоянии d = 1,5 см от левой пластины и b = 2,5 см от правой пластины. Заряд шарика равен q = − 0,2 нКл, масса шарика m = 20 мг. Шарик освобождают, и он начинает двигаться. На сколько успеет сместиться шарик по вертикали до удара об одну из пластин?

Решение

Рис. 264. Вертикальное смещение в электрическом поле

1. Так как шарик заряжен отрицательно, то он под действием силы Кулона | FK |= qE будет двигаться в направлении противоположном направлению век-

тора напряжённости электрического поля E					(рис. 264). До удара о левую пла-
стину шарик пролетит расстояние d с ускорением:
		a =	FK	= qE	;
			m
				m
2. Время полёта шарика до удара о пластину:
d =	aτ2		τ =		2dm	;
	2	;			qE

3. По вертикали шарик будет двигаться с ускорением свободного падения g, поэтому его координата за время τ изменится на величину y:

y =	gτ2	2dgm	=	dgm	1,5 10−2 10	2 10−5	0,075м ≡ 7,5 см;
	2	2qE		qE	2 10−10 2	105

102

265. На сколько градусов нагреется вода, если через кипятильник пройдёт электрический заряд q = 100 Кл? Напряжение на нагревателе U = 210 В, масса воды m = 500 г, удельная теплоёмкость воды с = 4200 Дж/(кг К).

	Решение
cm T = IU t =	q U t = qU;	T =	qU	=	100 210	=10K;
	t		cm		4200 0,5

266.К однородному медному цилиндрическому проводнику длиной l = 10

мприложили разность потенциалов U = 1 В. Определить промежуток времени,

в течение которого температура проводника изменится на Т = 10 К. Изменения сопротивления проводника и рассеяние тепла при нагревании не учитывать. Плотность меди ρ1 = 8900 кг/м3, удельное электрическое сопротивление меди ρ2 = 1,7 10 − 8 Ом м, удельная теплоёмкость меди с = 380 Дж/(кг К).

Решение

1. Масса проводника:

m = ρ1ls ;

2. Сопротивление проводника:

R= ρs2l;

3.Сохранение энергии применительно к нагреванию проводника:

cm T = IUτ =	U2	τ; cρ ls T =	U2sτ	; τ =	cρ ρ	l2	T	;
	R		ρ2l		1 2
		1			U2

τ = 380 8,9 103 1,7 10−8 102 10 57,5c ; 1

267. При замыкании на сопротивление R = 5 Ом батарея даёт ток силой I1 = 1 А. Сила тока короткого замыкания I КЗ = 6 А. Какую наибольшую полезную мощность может дать батарея?

Решение

1. Наибольшее значение мощности (см. задачу 2.227) составит:

Na(max) =

ε2R

;

= r;

Na(max) =

ε2r

ε2

;

(R + r)

2. Ток короткого замыкания:

ε;

IКЗ =

r =

;

IКЗ

3. Максимальная полезная мощность:

Na(max)

= 9 Вт;

КЗ

268. Два вертикально расположенных стержня, имеющие длину L = 1 м и диаметр d = 1 см сопротивление на единицу длины ρ = 1 10 − 5 Ом м, подсоединены через идеальный амперметр к источнику ЭДС ε = 1,5 В и внутренним сопротивлением r0 = 0,05 Ом. Скользящие контакты соединены с сопротивлением R = 0,1 Ом, которое в поле тяжести g начинает соскальзывать вдоль них из

103

верхней точки вниз без нарушения контакта, как показано на рисунке. В пренебрежении эффектами, связанными с магнитным полем, определить какое значение тока I покажет амперметр через время τ = 0,5 с после начала движения? Силу трения не учитывать.

Решение

	1. Запишем кинематические уравнения
	движения сопротивления, считая, что на
	него действует только сила тяжести и
	движение происходит	по вертикальной
	оси с нулевой начальной скоростью
	y = gt2	,
	2
Рис. 268. Скольжение сопротивления	и определим расстояние, которое пройдёт
	сопротивление за время τ

l= 5 02,52 = 0,625м .

2.Определим электрическое сопротивление одного отрезка стержня длиной

r = ρ	4l	=1 10	−5 4 0,625		0,08Ом.
	πd2			3,14 10−4

3. Электрическая схема установки, таким образом представит собой три последовательно включенных внешних сопротивления: R0 = R + 2r

и внутреннее сопротивление источника r0. Закон Ома для полной цепи в этом случае запишется так

I =	ε	=	1,5	4,8 A .
I =	R + 3r + r	=	0,1 + 0,16 + 0,05	4,8 A .
	0

269. К источнику с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно резистор с сопротивлением R = 8 Ом и плоский воздушный конденсатор, расстояние между пластинами которого d = 2 10 − 3 м. Какова напряжённость электрического поля между пластинами конденсатора?

Решение

Сила тока, протекающего через рези-

стор:

IR =

;

R + r

Падение напряжения на резисторе:

UR = IR R =

εR

;

Рис. 269. Напряжённость

R + r

электрического поля конденсатора

Поскольку UR = UC :

E = UC =

εR

9 8

= 4 103 В

≡

кВ

;

d(R + r)

10−3 (8 +1)

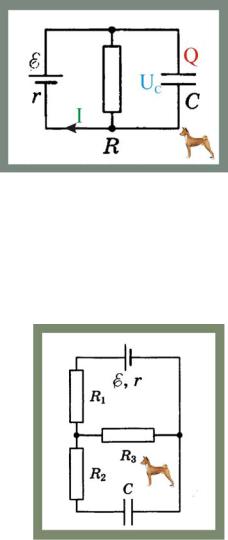
270. Найти электрический заряд конденсатора с С = 1 мкФ, если внутреннее сопротивление источника тока r = 2 Ом, его ЭДС ε = 24 В, R = 10 Ом

104

			Решение
1.	Сила тока, протекающего через рези-
стор:				ε
			IR =	ε		;
			IR =	R + r		;
				R + r
2.	Падение напряжения на резисторе:
		UR	= IR R =		εR		;
		UR	= IR R =		R + r		;
					R + r
3.	Поскольку UR = UC :								Рис. 270. Заряд конденсатора
Q = UCC =		εRC	= 24 10 1 103					= 2 10−2 Кл;
Q = UCC =		R + r	= 24 10 1 103					= 2 10−2 Кл;
		R + r		12

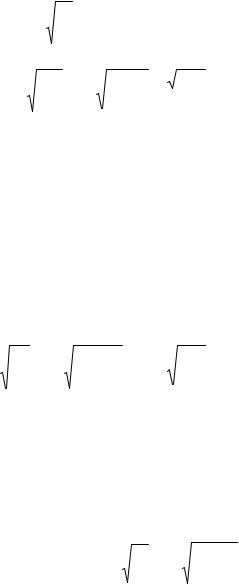
271. Конденсатор ёмкостью С = 2 мкФ присоединён к источнику постоянного тока с ЭДС ε = 3,6 В и внутренним сопротивлением r = 1 Ом. Внешняя цепь состоит из резисторов R1 = 4 Ом, R2 = 7 Ом, и R3 = 3 Ом. Каков заряд левой обкладки конденсатора?

Решение

1. Для постоянного тока конденсатор пред-

ставляет собой разрыв цепи, поэтому сила тока

через резисторы R1 и R3, включенные последо-

вательно с источником тока, определится как:

I =

;

R1 + R3 + r

2. Падение напряжения на резисторе R3:

U3 =

εR3

= UC ;

R1 + R3 + r

Рис. 271. Заряд конденсатора

3. Заряд пластин конденсатора:

q = UCC =

εR

3,6 3 2 10−6

= 2,7 10

−

6 Кл;

+ R

3 + r

4 + 3 +1

272. Проволочный виток, имеющий площадь s = 10 см2, разрезан в некоторой точке, и в разрыв включён конденсатор ёмкостью C = 10 мкФ. Конструкция помещена в магнитное поле, силовые линии которого перпендикулярны плоскости витка. Индукция магнитного поля равномерно убывает за t = 0,2 с на В = 0,01 Тл. Определить заряд на конденсаторе.

Решение

\| q \|= εiC =	B sC =	10−2	10−3 10−5	= 5 10−10 Кл;
	t	0,2

105

5. Колебания и волны

273. Первый математический маятник совершает колебания с частотой ν = 6 Гц. Длина нити второго маятника больше длины первого в ζ =3,24 раза. Чему равен период колебаний второго маятника?

Решение

Длина первого маятника:

= 1 =

2π

;

4π2ν2

Период колебаний второго маятника:

= 2π

ζl1

= 2π

3,24

= 0,3с;

4π2ν2

274. Тело массой m = 0,3 кг подвешено к двум параллельным пружинам с коэффициентами жёсткости k1 = 500 Н/м и k2 = 250 Н/м. Определить период собственных колебаний системы.

Решение

1. Пружины соединены параллельно, их деформация одинакова: x1 = x2 = x .

2. Сила, действующая на тело со стороны пружин, определится в виде суммы:

F = F1 + F2 , или k0 x = k1 x + k2 x; k0 = k1 + k2 ; 3. Период колебаний системы:

T = 2π	m	= 2π	m	= 6,28	0,3	= 0,1256c;
			k1 + k2		750
	k0

275. Пружинный маятник жёсткостью k = 2 103 Н/м совершает гармонические колебания. Масса груза m = 5 10 − 2 кг. Максимальная скорость груза vm = 20 м/с. Определить амплитуду колебаний маятника.

Решение

1. Закон сохранения энергии для гармонически колеблющегося тела:

mv2	kA2	;	A = v		m	= 20	5 10−2	= 0,1м;
m =	2			m	k		2 103
2

276. Задан график изменения кинетической энергии в функции времени колеблющегося гармонически тела. Чему равна полная механическая энергия в момент времени, соответствующий точке А графика?

106

Решение

1.Получим дифференциальное уравнение колебаний маятника на основе анализа движения с энергетических позиций. Это удобно сделать на примере частицы известной массы, находящейся в потенциальной яме.

2.Наглядной моделью такой системы может служить металлический шарик внутри криволинейной поверхности (рис.275.2). При смещении массы из состояния равновесия из положения 1 в положение 2 система приобретает запас потенциальной энергии. Если шарик считать материальной точкой, а положение статического равновесия 1 совместить с минимальным значением потенциальной энергии, то

Π2 = mgh .

3.Если далее шарик отпустить без

начальной скорости, то он начнёт двигаться в сторону минимизации потенциальной энергии, причём по мере опускания шарика относительно нулевого уровня потенциальной энергии, будет происходить её трансформация в кинетическую энергию.

Рис. 276.1. Энергия колебаний

Рис. 276.2. Потенциальная энергия

4.В точке 1 потенциальная энергия станет равной нулю, шарик будет обладать только кинетической энергией, которая затем снова начнёт преобразовываться в потенциальную энергию.

5.В точке 3 энергия шарика снова станет только потенциальной. Если пренебречь потерями на сопротивление и трение, то шарик будет бесконечно долго перемещаться внутри потенциальной ямы, совершая гармонические собственные незатухающие колебания.

6.Применительно к массе, скреплённой с горизонтальной пружиной, изменение потенциальной энергии определится уравнением:

П = kx22 ,

величина х в конкретном случае зависит от положения массы, которая будет совершать движение в пределах потенциальной ямы. Потенциальную яму любой формы можно представить в виде функции смещения, аппроксимируя её степенным рядом:

П(x)= ax2 + bx3 + cx +K,

При малых отклонениях х2 >>х3 >>х4, с учётом этого П(x) ax2 .

7. В рассматриваемом случае, при растяжении и сжатии пружины, её по-

107

8. Проекция действующей силы для консервативных механических систем связана с потенциальной энергией известным соотношением:

Fx = − ∂П∂x(x) = −2ax = −kx ;

9. Уравнение совпадает со значением возвращающей силы. Перепишем уравнение следующим образом:

&&		&&	2
Fx = −kx , mx	+ kx = 0 , mx		+ ω mx = 0,
или окончательно	x + ω x = 0 .
	&&	2

10. Рассмотрим далее энергетические особенности гармонических незатухающих собственных колебаний.

Отметим, что упругая сила и сила тяжести относятся к консервативным силам, работа которых не зависит от вида траектории, а определяется только положением начальной и конечной точки, т.е. для массы, соединённой с горизонтальной пружиной можно записать

∫Fупрdl = 0 .

11. Полная энергия колеблющейся массы должна оставаться постоянной, т.е. справедлив закон сохранения энергии. В процессе колебаний происходит преобразование потенциальной энергии в кинетическую энергию. На дне потенциальной ямы масса обладает только кинетической энергией, которая имеет максимальной значение. В крайних положениях массы энергия имеет потенциальный характер

		2			&		2		mx	2	ω	2
E2,3 = Пmax	= kx	0	,	E1 = Kmax	=	mx	0	=		0			.

	2				2			2

12. Установим закон изменения кинетической и потенциальной энергии в случае гармонического колебания, для этого запишем уравнения кинетической и потенциальной энергии:

	2		&2	2	2
K(t)= mv	=	mx		= mx0ω	sin2 (ωt + ϕ0 ),
K(t)= mv	=			= mx0ω	sin2 (ωt + ϕ0 ),
2			2	2
П(t)= kx2			= kx02 cos2		(ωt + ϕ0 ),
	2			2		k на mω2 , и складывая
13. Заменяя в уравнении потенциальной энергии						k на mω2 , и складывая
уравнения, получим:
E = K +	П = kx02			= mx02ω2 , E =		E .
			2	2		2

14ю Периодичность изменения энергии установим, переписав уравнения кинетической и потенциальной энергии в соответствии с тригонометрическими

правилами:		1			1
K(t)= Kmax sin	2			−			,
		(ωt + ϕ0 )= Kmax	2		2	cos 2(ωt + ϕ0 )

	2	1		+	1		,
П(t)= Пmax cos		(ωt + ϕ0 )= Пmax	2		2	cos 2(ωt + ϕ0 )

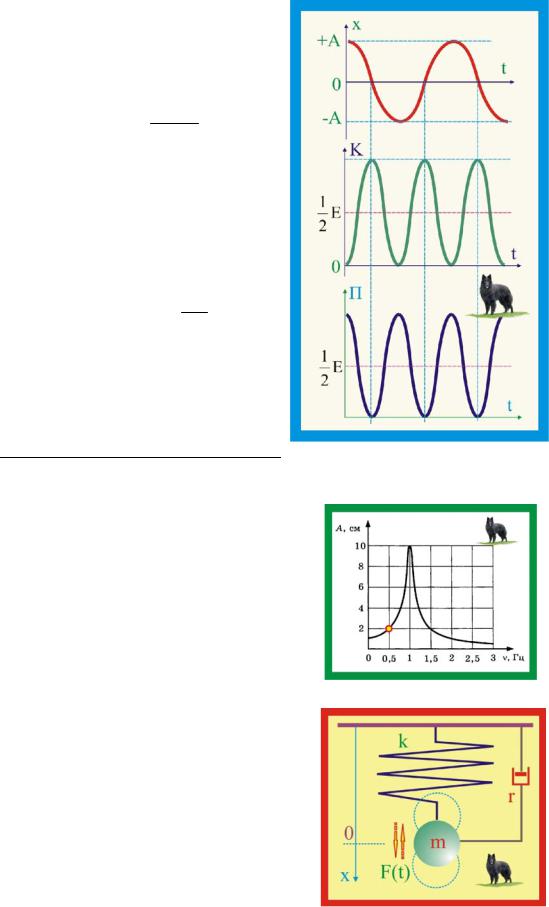
очевидно, что кинетическая и потенциальная энергии изменяются с частотой 2ω, в два раза превышающей частоту колебаний. В моменты амплитудного значения смещения кинетическая энергия обращается в нуль, а полная энергия колебаний равна наибольшему значению потенциальной энергии (рис. 276.3)

108

E = Пmax =	kA2	.
	2

15. При прохождении системой положения равновесия при х = 0, полная энергия является кинетической

= = mA2ω2

E Kmax 2 .

16.Разумеется, что в отсутствие сопротивления значение максимальной кинетической энергии совпадает со значением максимальной потенциальной энергии колебательной системы.

17.Средние значения кинетической

энергии

< K > и

потенциальной

<Π >равны половине полной энергии

<K >=< Π >= E2 = kA4 2 .

18.Возвращаясь к рис. 276.1 отменим, что на основании приведенных выше сведений:

Πmax = Κmax =160Дж;

ΚA =120Дж; ΠA = 40Дж;

ΕA = ΚA + ΠA =160Дж;

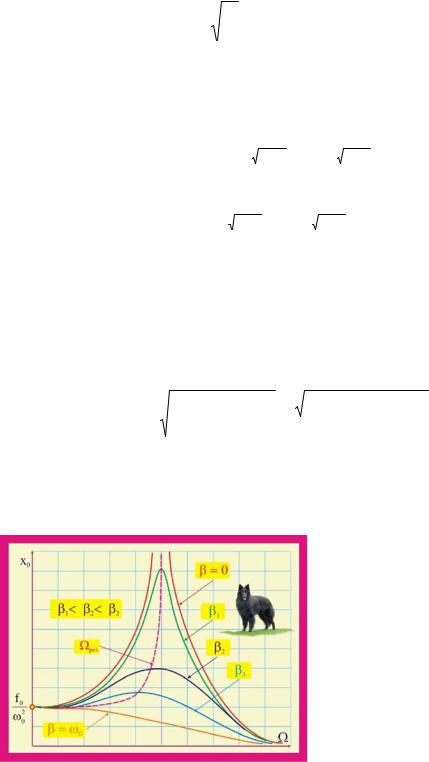
277.Приведена зависимость возвращающей силы установившихся колебаний маятника (резонансная кривая). Определить отношение амплитуды установившихся колебаний маятника на резонансной частоте к амплитуде колебаний на частоте

ν= 0,5 Гц.

Решение

1.На практике часто требуется колебания поддерживать, что возможно при сообщении колебательной системе энергии от внешнего источника. Такие колебания классифицируются как вынужденные колебания.

2.Рассмотрим колебательную систему в виде массы, соединённой с вертикально расположенной пружиной (рис. 277.2). Помимо силы сопротивления к массе приложена внешняя периодическая сила F(t). Уравнение движения в этом случае запишется следующим образом: ).m&x&+ rx& + kx = F(t

3. Рассмотрим случай, когда внешняя

Рис. 276.3. Зависимость смещения и энергии от времени

Рис. 277.1. Резонансная кривая

Рис. 277.2. Вынужденные колебания

109

возбуждающая сила изменяется по гармоническому закону с частотой Ω, например, по закону косинуса:

F = F0 cosΩt .

4. Уравнение движения в этом случае перепишется в виде: m&x&+ rx& + kx = F0 cosΩt .

5. Введём следующие обозначения:

ω0 =	k	,	β =	r	.	f0 =	F0	,
							m
	m			2m
что позволяет уравнение движения переписать в виде
&&	&		2
x + 2βx			+ ω0 x = f0 cosΩt .

5. Неоднородное дифференциальное уравнение имеет решение в виде суммы общего решения одноимённого однородного уравнения х1 и частного решения х2 неоднородного уравнения, причём:

x1 = e

−βt

t β2 −ω02

+ C2e

−t β2 −ω02

C1e

= x0 cos(Ωt −ϕ),

x = x

+ x

= e−βt C et

β2 −ω02 + C

e−t β2 −ω02

+ x

cos(Ωt −ϕ).

6. Первый член уравнения x(t) характеризует свободные затухающие колебания. Постоянные интегрирования С1 и С2, как обычно, определяются путём подстановки начальных условий х(0) и x&(0) , имеющих место при t = 0. Второй

член этого уравнения описывает стационарные вынужденные колебания, происходящие с частотой вынуждающей внешней силы Ω с амплитудой, определяемой уравнением:

x0 =

−Ω

+ Ω

r2 +

−Ωm

(

)

7. Сдвиг фазы колебаний относительно внешней силы равен:

ϕ = arctg

= arctg

2Ωβ

−Ωm

ω2 −Ω2

8. Для случая малого затуха-

ния, т.е. при β→0 уравнение х0

возможно упростить:

x0 =

;

ω02 −Ω2

1−

9. Очевидно, что при ω0 = Ω,

A→∞, но этот случай довольно

далёк от реальности, затухание

при колебаниях всегда имеет ме-

сто быть. Вместе с тем уравне-

Рис. 277.3. Частотные характеристики

ние x0 =f(Ω) позволяет устано-

вить

некоторые

характерные

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2311 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>