ДИФУР ГУРЕВИЧ ЛЕКЦИИ

Замечание. Если 2 = 1, то фазовыми траекториями являются

1

ветви гипербол и полуоси.

В общем случае, когда векторы V1 è V2 не ортогональны, качественное

поведение фазовых траекторий изображено на рис. 8.6. Определение. Особая точка в рассмотренном случае называется

седлом.

8.4.Фокус

Предположим, что 1 = + i ; 2 = i ; > 0; > 0 (случай< 0 рассматривается аналогично и дает то же поведение фазовых

траекторий).

Пусть комплексный вектор V = V1 + iV2 является собственным век- тором матрицы A, соответствующим собственному значению 1. Тогда вектор V = V1 iV2 будет собственным вектором, соответсòâующим собственному значению 2. Из линейной независимости V и V следует линейная независимость вещественных векторов V1 è V2.

Согласно теории линейных систем дифференциальных уравнений (см. теорему 6.7) любое ненулевое решение системы (8.6) имеет вид

Y (t) = c1Re(e 1tV ) + c2Im(e 1tV ):

Отсюда, вычисляя указанные действительные и мнимые части, получа- ем, что

Y (t) = e t(c1 cos t + c2 sin t)V1 + e t( c1 sin t + c2 cos t)V2; (8.11)

ãäå c1, c2 некоторые числа, c21 + c22 6= 0:

Предположим сначала, что векторы V1 è V2 образуют ортонорми- рованный базис. Перейдем в плоскости x0y к прямоугольной системе

координат v10v2, оси которой направлены вдоль V1 è V2 (ñì. ðèñ. 8.1). Соотошения (8.11) в координатной форме примут вид

Эти уравнения можно записать в виде

151

уравнения (8.12) параметрические уравнения логарифмической спирали с центром в начале координат. Следовательно, фазовые траектории имеют вид, изображенный на рис. 8.7.

В общем случае, когда векторы V1 è V2 не образуют ортонормирован-

ный базис, качественное поведение фазовых траекторий представлено на рис. 8.8.

Определение. Особая точка в рассмотренном случае называется фокусом.

8.5.Центр

Предположим, что корнями уравнения (8.7) являются 1 = i ; 2 = = i ; > 0:

Рассуждая так же, как в предыдущем разделе 8.4, снова приходим к уравнениям (8.12), которые при = 0 определяют окружность с цен-

тром в начале координат. Следовательно, качественное поведение фазовых кривых в общем случае имеет вид, показанный на рис. 8.9.

Ðèñ. 8.9

Определение. Особая точка в рассмотренном случае называется центром.

152

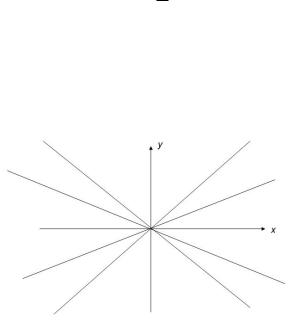
8.6.Дикритический узел

Пусть кратный корень уравнения (8.7), которому соответствуют

два линейно независимых собственных вектора V1 è V2. Любой вектор V 2 R2 представим в виде V = 1V1 + 2V2. Отсюда следует, что AV =

= V или (A E)V = 0 (E единичная матрица). Это возможно тогда и только тогда, когда A E = 0, т.е.

Другими словами, c = b = и a = d = 0. Уравнение (8.2) в этом случае имеет вид

а его решением будет y = cx, c произвольная константа. Интеграль-

ными кривыми являются лучи, выходящие из начала координат (рис. 8.10).

Ðèñ. 8.10

Определение. Особая точка в рассмотренном случае называется дикритическим узлом.

8.7.Вырожденный узел

Рассмотрим последний из возможных случаев. Пусть единственное собственное значение матрицы A и ему соответствует нормирован- ный собственный вектор V1, причем все остальные собственные векторы линейно зависимы с V1.

Теорема 8.2. Существует вектор V2, линейно независимый с V1, òà-

153

(этого всегда можно добиться, перейдя к новой системе координат, одним из базисных векторов которой является V1). В этом случае равенство AV1 = V1 перейдет в равенство

=:

a 0

Следовательно,

Собственными значениями этой матрицы являются и b. В силу единственности собственного значения b = . Кроме того, d 6= 0, т.к. в противном случае у A было бы два линейно независимых собственных вектора:

Отсюда следует, что в качестве V2 можно взять вектор

0

V2 = 1 :

d

Теорема доказана. Теорема 8.3. Вектор-функции

Y1(t) = etV1; Y2(t) = et(tV1 + V2)

образуют фундаментальную систему решений уравнения (8.6). Доказательство. Непосредственная проверка показывает, что

Y1(t); Y2(t) решения (8.6). Их линейная независимость следует из того, что при t = 0 определитель Вронского

jY1(0) Y2(0)j = jV1 V2j =6 0:

Теорема доказана.

Из теоремы 8.3 следует, что любое ненулевое решение системы (8.6) имеет вид

ãäå c1; c2 некоторые числа, c21 + c22 6= 0.

154

Предположим сначала, что векторы V1 è V2 образуют ортонорми- рованный базис. Перейдем в плоскости x0y к прямоугольной системе

координат v10v2, оси которой направлены вдоль V1 è V2 Соотношения (8.14) в координатной форме примут вид

Åñëè c2 = 0, à c1 > 0, то фазовой траекторией будет положительная часть оси v1. Åñëè c2 = 0, à c1 < 0, то фазовая траектория отрицательная часть оси v1.

Пусть теперь c2 > 0. Предположим также, что c1 0; > 0 (другие случаи рассматриваются аналогично). Когда t меняется от 0 до 1, v1(t) возрастает от c1 äî 1, à v2(t) возрастает от c2 до 1. При t, меняющихся

c1, à ïðè t 2 ( 1; t0] v1(t) возрастает от v1(t0) до 0. Из этих элемен-

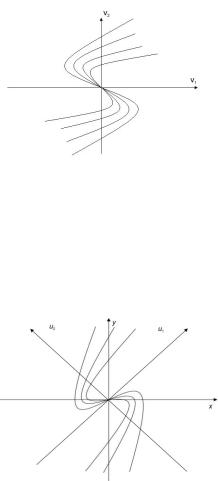
тарных рассуждений заключаем, что фазовые траектории имеют вид, показанный на рис. 8.11.

Ðèñ. 8.11

В общем случае, когда V1 è V2 не образуют ортонормированного ба-

зиса, качественное поведение фазовых траекторий представлено на рис. 8.12.

Ðèñ. 8.12

Особая точка в рассмотренном случае называется вырожденным узлом.

155

9.Уравнения в частных производных

первого порядка

Теория уравнений в частных производных первого порядка тесно связана с теорией систем обыкновенных дифференциальных уравнений. Изложим вначале необходимые сведения, касающиеся систем обыкновенных дифференциальных уравнений. Рассмотрим нормальную систему

где функции f1; : : : ; fn определены в некоторой области D Rn+1.

9.1.Сведение системы уравнений

êодному уравнению высшего порядка

Один из методов решения системы состоит в следующем. Предположим, что функции y1(x); : : : ; yn(x) образуют решение системы (9.1) на интервале (a; b) и функции f1; : : : ; fn имеют непрерывные частные производные до (n 1)-го порядка включительно. Продифференцируем первое

из тождеств

yk0 fk(x; y1(x); : : : ; yn(x)); k = 1; : : : ; n;

последовательно n 1 раз по x, в результате получим тождества

y1(m) 'm(x; y1(x); : : : ; yn(x)); m = 1; : : : ; n;

Подставив эти соотношения в правую часть последнего уравнения системы (9.2), получим уравнение

шения системы (9.1), то y1(x) решение уравнения (9.4). Обратно, если

156

y1(x) решение уравнения (9.4), то, определяя функции y2(x); : : : ; yn(x) по формулам (9.3), можно показать, что функции y1(x); : : : ; yn(x) îáðà-

зуют решение системы (9.1), и, следовательно, система (9.1) равносильна уравнению (9.4). А это означает, что решение системы (9.1) сводится к решению (9.4).

Замечание 1. Если формулы (9.3) получить невозможно, то в ка-

честве исходного тождества в этих рассуждениях можно взять какоенибудь другое, например, y20 f2(x; y1(x); : : : ; yn(x)).

Замечание 2. Существование соотношений (9.3) устанавливается с помощью следующей теоремы о неявных функциях.

Теорема 9.1. Пусть T = (t1; t2; : : : ; tm), Y = (y1; y2; : : : ; yn),

F (T; Y ) = (F1; F2; : : : ; Fn), функции Fi(T; Y ) (i = 1; : : : ; n) определены и непрерывны в области G Rm+n вместе с частными производны-

Тогда уравнение F (T; Y ) = 0 определяет однозначную неявную векторфункцию Y = (T ), определенную и непрерывную вместе с частными производными первого порядка в некоторой окрестности точки T0, причем (T0) = Y0.

9.2. Решение системы обыкновенных дифференциальных уравнений

с помощью первых интегралов

Определение 9.1. Функция (x; y1; : : : ; yn) называется первым интегралом (или просто интегралом) системы (9.1), если:

1) функция не равна тождественно постоянной;

2) в области D функция непрерывна вместе с частными производ-

ными по всем переменным;

3) вдоль любого решения y1(x); : : : ; yn(x) системы (9.1) функция принимает постоянное значение, т. е.

(x; y1(x); : : : ; yn(x)) const:

Иногда первым интегралом называют не функцию (x; y1; : : : ; yn), а соотношение

(x; y1; : : : ; yn) = c;

где c константа.

157

Пример 9.1. Вращение твердого тела вокруг неподвижной точки описывается следующей системой дифференциальных уравнений:

ãäå y1(t); y2(t); y3(t) составляющие вектора угловой скорости в момент времени t; A, B, C известные положительные числа. Умножая эти уравнения соответственно на Ay1, By2, Cy3

Ay1y_1 + By2y_2 + Cy3y_3 = 0;

èëè

dtd (Ay12 + By22 + Cy32) = 0:

Следовательно, функция

1(y1; y2; y3) = Ay12 + By22 + Cy32

является первым интегралом системы (9.5). Если уравнения (9.5) умножить соответственно на A2y1; B2y2; C2y3 и сложить, то получим ещ¼ один

первый интеграл:

2(y1; y2; y3) = A2y12 + B2y22 + C2y32:

Если известен первый интеграл (x; y1; : : : ; yn) системы (9.1), то е¼ порядок можно понизить. В самом деле, предположим, что соотношение

(x; y1; : : : ; yn) = c

неявно определяет функцию

yn = '(x; y1; : : : ; yn 1):

Подставляя эту функцию в первые n 1 уравнения системы (9.1), мы получим систему относительно y1; : : : ; yn 1.

В примере (9.1) были найдены два первых интеграла 1(y1; y2; y3)

è2(y1; y2; y3). Если предположить, что A > B, то из соотношений

Ay12 + By22 + Cy32 = c1;

158

A2y12 + B2y22 + C2y32 = c2

можно,предполагая, например, y1 è y2 неотрицательными, выразить y1 è y2 как функции, зависящие от y3, c1 è c2. Подставив эти функции в третье уравнение системы (9.5), получим дифференциальное уравнение первого порядка относительно y3. Если же в этом примере A = B = C, то второй интеграл 2(y1; y2; y3) не будет содержать новой информации.

В связи с этим введем следующее определение.

Определение 9.2. Первые интегралы f i(x; y1; : : : ; yn)gmi=1 (m n)

системы (9.1) называются независимыми, если в области D матрица

можно выразить m функций через оставшиеся n m функций и кон-

станты c1; : : : ; cm и свести систему (9.1) к дифференциальной системе из n m уравнений.

Рассмотрим подробно случай m = n. Выберем произвольную точку

Y = (y1; : : : ; yn), T0 = (x0; c01; : : : ; c0n), Y0 = (y10; : : : ; yn0), Fi = i ci, i = 1; : : : ; n. Согласно этой теореме, система (9.6) определяет неявно

однозначные непрерывно дифференцируемые функции

x0, S некоторая окрестность вектора (c1; : : : ; cn). По построению выполняются тождества

i(x; '1(x; c1; : : : ; cn); : : : ; 'n(x; c1; : : : ; cn)) ci; i = 1; : : : ; n:

Предположим, что через каждую точку некоторой окрестности точки (x0; y10; : : : ; yn0) проходит единственная интегральная кривая (т. е. график

решения) системы (9.1). По определению первых интегралов функции i; : : : ; n вдоль этих кривых принимают постоянные значения. В силу

159

единственности неявных функций (9.7) при достаточно малых и S ин-

тегральные кривые совпадают с кривыми, определяемыми уравнениями (9.7).

Таким образом, формулы (9.7) определяют решения системы (9.1), причем при надлежащем выборе констант c1; : : : ; cn можно получить

любое решение, график которого лежит в некоторой окрестности точ- ки (x0; y10; : : : ; yn0).

Определение 9.3. Система n независимых первых интегралов си-

стемы (9.1) называется общим интегралом системы (9.1).

Заметим, что знание общего интеграла системы (9.1) позволяет получить все е¼ решения в неявном виде (9.6).

Теорема 9.2 (о существовании общего интеграла). Пусть функции f1; : : : ; fn в системе (9.1) непрерывно дифференцируемы в окрестности точки (x0; y10; : : : ; yn0). Тогда у системы (9.1) существует общий интеграл, определенный в некоторой окрестности этой точки.

Доказательство. По теореме о дифференцируемости решения зада- чи Коши по начальным данным существуют непрерывно дифференцируемые функции 'i(x1; x2; : : : ; xn+2), i = 1; : : : ; n, определенные в области

S ( , S некоторые окрестности точек x0 è (y10; : : : ; yn0 ) соответственно), такие что формулы

yi(x) = 'i(x; c0; c1; : : : ; cn); i = 1; : : : ; n;

определяют на интервале решение задачи Коши для системы (9.1), удовлетворяющее начальным условиям

yi(c0) = ci; i = 1; : : : ; n;

для любой точки (c0; c1; : : : ; cn) 2 S. Определим функции

i(x; y1; : : : ; yn) = 'i(x0; x; y1; : : : ; yn); i = 1; : : : ; n:

Очевидно, функции i непрерывно дифференцируемы в окрестности точки (x0; y10; : : : ; yn0). Из определения функций 'i следует, что вдоль лю- бого решения '~1(x); : : : ; '~n(x) системы (9.1), график которого лежит в области S, выполняются тождества

i(x; '~1(x); : : : ; '~n(x)) '~i(x0); i = 1; : : : ; n:

Следовательно, функции i(x; y1; : : : ; yn), i = 1; : : : ; n, образуют систему

160