Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет путей сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

met_ukazmatem_k_r__1-3

.pdf

Скачиваний:

Добавлен:

09.06.2015

Размер:

181.57 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

КОНТРОЛЬНАЯ РАБОТА № 3

Неопределенный и определенный интегралы. Функции нескольких переменных.

8.2.1–8.2.10. Найти неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.

а) ∫esin2 x sin 2xdx ;

б) ∫arctg

8.2.1.

xdx;

в)

∫

;

г) ∫

3 +

+ 3 x + 1

8.2.2.

а) ∫

xdx

;

б) ∫ex ln(1+ 3ex )dx;

(x2 + 4)6

∫

2x2 − 3x +1

г) ∫

в)

dx ;

x3 +

sin x + tg x

8.2.3.

а)∫

x3dx

;

б) ∫x3xdx;

1− x8

в)

∫

(3x − 7)dx

;

г) ∫

3 + 4x2 + 4x +

x + 3

+ 3 (x + 3)2

8.2.4.

а) ∫

;

б) ∫

arcsin x

dx;

cos2 x(3tg x +1)

1− x2

2 +

в)

∫

;

г) ∫

1+ x

dx .

3 + x2

+ 2x + 2

3 1+ x

8.2.5.

а) ∫

cos3xdx

;

б) ∫x2 e3x dx;

4 + sin3x

в) ∫

x2dx

;

3 + 5x2 +

8x + 4

8.2.6.

а) ∫

sin xdx

;

3 cos2 x

в) ∫

(x + 3)dx

;

3 + x2 − 2x

8.2.7.

а) ∫

(x + arctg x)dx

;

1+ x2

в) ∫

(x2 − 3)dx

;

4 + 5x2 +

г) ∫	cos xdx						.

	1+ cos x
б) ∫xarcsin						1		dx ;

							x

г) ∫	(4		x		+1)dx
									.


	(	x		+ 4)4 x3

б) ∫xln(x2 +1)dx ;

x + 5dx

г) ∫1+ 3x + 5 .

8.2.8.

а) ∫

arctg

dx;

б) ∫xsin xcos xdx ;

x(1+ x)

в)

∫

x2dx

;

г)

∫

4 − 81

3cosx + 4sin x

8.2.9.

а) ∫

sin xdx

;

б) x2 sin 4xdx;

3 3 + 2cosx

∫

(x2 − x +1)dx

∫

(

−1)(6

+1)dx

в)

;

г)

+ 2x2 − 3

3 x

8.2.10. а) ∫

4 + ln x

;

б) ∫xln2 xdx;

в)

∫

2 − 6)dx

;

г)

∫

2sin x + cos x +

+ 6x2 + 8

8.2.21–8.2.30. Вычислить определенные интегралы.

2			1
8.2.21. ∫xsin xdx;			8.2.22. ∫xarctgxdx.
0			0
2	ln x		1		5x +1
8.2.23. ∫		dx.	8.2.24. ∫			dx.
8.2.23. ∫	x	dx.	8.2.24. ∫	x2 + 2x +1		dx.
1			0
π			2
8.2.25. ∫sin 2xcos2 xdx.			8.2.26. ∫		x ln xdx.
0			1

2dx

8.2.27.∫0 sin x + cosx.

8.2.29. ∫0 x2 + x +1.

8.2.28. ∫xln(1+ x)dx.

2
8.2.30. ∫2		xdx		.

	1− x		4
0	1− x

8.2.71–8.2.80. Решить указанные задачи с помощью определенного интеграла.

8.2.71. Вычислить площадь фигуры, ограниченной параболой у=3х2+1 и прямой у=3х+7.

8.2.72.Вычислить площадь фигуры, ограниченной одной аркой циклоиды х=а(t–sin t), у=а(1–соs t) (0 ≤ t ≤ 2π) и осью Ох.

8.2.73.Вычислить площадь фигуры, ограниченной кардиоидой

r= 3(1+соs φ).

8.2.74.Вычислить площадь фигуры, ограниченной четырехлепестковой розой r=4sin 2φ.

8.2.75.Вычислить объем тела, образованного вращением вокруг оси Ох

фигуры, ограниченной параболами у=х2 и у= 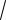х .

8.2.76. Вычислить объем тела, образованного вращением вокруг оси Ох

фигуры, ограниченной полуэллипсом у=3 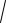1− х2 , параболой х= 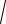1− у и осью Оу.

8.2.77.Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми y=2/(1+х2) и у=х2.

8.2.78.Вычислить длину дуги полукубической параболы y= (х − 2)3 от

точки A(2; 0) до точки B(6; 8).

8.2.79.Вычислить длину кардиоиды r=3(1–соs φ).

8.2.80.Вычислить длину одной арки циклоиды х=3(t–sin t), у=3(1–соs t)

(0 ≤ t ≤ 2π).

9.1.1–9.1.10. Найти производные функции двух переменных.

9.1.1.

∂z

если

z = usin(uv),

где

u =

v = x − y .

∂x

9.1.2.

если

z = vcos(

) ,

где

u = t2 ,

v = sint .

9.1.3.

∂z

если xy2 z3 − z2 + xz − y + x = 0 .

∂y

9.1.4.

∂z

, если z = u2vlnv , где u = xy ,

v = x + y .

∂x

9.1.5.

если

z = uv2 lnu ,

где

u = t3 ,

v = cost .

9.1.6.∂z , если xy2 z2 + z2 x + x − 2y + 3 = 0 .

∂y

	∂z
9.1.7.			, если z = u		u2 − v2 , где		u = x + 2y , v = −x + y .

	∂x
	dz
9.1.8.		,		если z = v		u − v , где u = sin 2t , v = t3 .

	dt
9.1.9.	∂z			, если e z 2 − xy 2 z 3 + xz			− x = 0 .
	∂y

	∂z
9.1.10.	∂z		, если z = u 1− uv , где u = xy , v = x + 2y .
9.1.10.			, если z = u 1− uv , где u = xy , v = x + 2y .
	∂x
9.1.61–9.1.70. Вычислить двойной интеграл.
9.1.61.	∫∫			0 ≤ x ≤ 2
	∫∫
		2xydxdy ; где область D – прямоугольник				.
	D			0	≤ y ≤ 3
9.1.62. ∫∫xydxdy ; где область D ограничена параболой y = x2							и прямыми
	D
x =1, y = 0 .
9.1.63.	∫∫			0 ≤ x ≤ 3
	∫∫
		xydxdy ; где область D – прямоугольник				.
	D			0 ≤ y ≤ 2
9.1.64.	∫∫			0 ≤ x ≤1
	∫∫
		xy2dxdy ; где область D – прямоугольник			≤ y ≤	.
	D			0	≤ y ≤	2
9.1.65.	∫∫			0 ≤ x ≤1
	∫∫
		x2 ydxdy ; где область D – прямоугольник			≤ y ≤	.
	D			0	≤ y ≤	4
9.1.66.	∫∫			0 ≤ x ≤ 4
	∫∫
		xy3dxdy ; где область D – прямоугольник			≤ y ≤	.
	D			0	≤ y ≤	1
9.1.67. ∫∫x2 ydxdy ; где область D ограничена параболой y = x2 и прямыми
	D
x =1, y = 0 .
9.1.68. ∫∫xy2dxdy ; где область D ограничена параболой y = x2							и прямыми
	D
x =1, y = 0 .
9.1.69.	∫∫				0 ≤ x ≤1
	∫∫
		(x +1)ydxdy ; где область D – прямоугольник					.
	D				0 ≤ y ≤		2
9.1.70.	∫∫				0 ≤ x ≤1
	∫∫
		(x2 +1)y2dxdy ; где область D – прямоугольник					.
	D				0	≤ y ≤ 3

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016112.64 Кб13metod_ukaz_pismennih_rabot.doc
#
09.06.2015737.28 Кб34Met_Credo_GR.doc
#
09.06.2015336.38 Кб3MET_EMM.DOC
#
09.06.2015290.82 Кб7Met_po_ekonomich_teorii_dlya_ekonom_-logistov.doc
#
08.06.2015416.26 Кб28Met_ukazania_po_vypolneniyu_k_r_po_rus_yaz__2.doc
#
09.06.2015181.57 Кб7met_ukazmatem_k_r__1-3.pdf
#
09.06.2015445.16 Кб26met_ukaz_fizikak_r__1-2.pdf
#
09.06.2015449.57 Кб68met_ukaz_k_r__1-4_i_svod_k_r__1-2_Angl.pdf
#
09.06.2015668.84 Кб17Microeconomics.docx
#
09.06.2015610.3 Кб46moy_praktikum.doc
#
09.06.201511.97 Mб30MPT_UP4_end_ZEI.pdf