fiz

Чтобы лучше разобраться с направлением вектора напряженности E , обратимся к рис. 97-2. На этом рисунке изображен положительный заряд источник qист , в поле которого располагается точка М. Если в эту точку

внести пробный (положительный) заряд qпр , то на него будет действовать

сила F , направленная в сторону от заряда-источника. Но поскольку условились считать вектор напряженности E сонаправленным с вектором силы F , действующей на

положительный пробный заряд, значит, вектор E направлен в точке М так, как показано на рис. 97-2, и когда в точке М никакого пробного заряда нет.

Если не говорится о знаке заряда-источника, то его принято считать

из точки М, то поле в этой точке все равно останется и оно будет иметь направление, показанное силой

F , когда заряд в ней был. Это направление указывает на рис. 97-3 вектор напряженности E (говорят «направление поля» или «направление вектора напряженности», имея в виду одно и то же).

Таким образом, если заряд-источник электрического поля положительный, то вектор напряженности E во всех точках этого поля «отворачивается» от заряда-источника, а если заряд-источник

отрицательный, то вектор напряженности E во всех точках окружающего его поля «поворачивается» к такому заряду. При этом вектор напряженности не изменяется, какие бы знака пробные заряды ни вносили в это поле.

Единица напряженности электрического поля в СИ – Н/Кл или В/м. Физический смысл единицы измерения Н/Кл: 1 Н/Кл – напряженность электрического поля в такой точке, в которой на пробный заряд 1 Кл действует сила 1 Н.

Как уже было сказано, напряженность электрического поля в данной точке не зависит ни от величины и знака пробного заряда, внесенного в него, ни от величины силы, действующей на этот пробный заряд. Если пробный заряд изменить в несколько раз, то во столько же раз изменится и сила, действующая на него, но величина напряженности поля при этом не изменится. Определим, от чего

зависит напряженность E электрического поля, созданного точечным зарядом-источником qист в некоторой точке М, отстоящей на расстоянии г от заряда-источника. Если в точку М поместить пробный заряд qпр , то на него со стороны заряда-источника qист будет действовать сила F , которой в случае, если оба заряда точечные по закону Кулона равен:

Fk qист qпр

r2

Так как по определению напряженности (см. формулу (97.1))

Согласно формулам (97.2) и (97.3) напряженность электрического поля точечного зарядаисточника в некоторой точке поля прямо пропорциональна величине этого заряда и обратно пропорциональна квадрату расстояния .между этой точкой поля и зарядом-источником. Кроме того, она зависит от диэлектрических свойств среды, в которой находится заряд-источник.

Подчеркнем еще раз, что в этих формулах qист и qист – модуль заряда-источника поля.

Таким образом, напряженность поля, созданного точечным зарядом-источником, зависит от величины и знака этого заряда, от расстояния между этим зарядом и точкой поля, в которой определяется напряженность, и от среды, в которой заряд находится.

По формулам (97.2) и (97.3) можно также определить напряженность поля заряженной сферы, если заряд по ней распределен равномерно. В этом случае r – расстояние от точки поля, в которой определяется напряженность, до центра сферы.

Следует иметь в виду, что в задачах электростатики прямо не указывается, о каких зарядах идет речь, пробных или источниках, об этом нужно самим догадаться, анализируя условие задачи. Если сказано, что в поле такого-то заряда что-то происходит, то этот заряд-источник поля, а если сказано, что такой-то заряд внесли в поле или что он там движется или на такой-то заряд действует сила и т. п., то этот заряд – пробный.

Если электрическое поле создано несколькими зарядами-источниками, то результирующая напряженность этого поля определяется принципом суперпозиции полей.

Принцип суперпозиции полей: напряженность электрического поля E , созданного в данной точке несколькими зарядами-источниками, равна векторной сумме напряженностей полей Ei , созданных в этой точке каждым зарядом в отдельности:

E N Ei .

i 1

На рис. 97-4 применен принцип суперпозиции полей для определения напряженности E поля, созданного в точке М двумя точечными зарядами q1 и q2 (двумя положительными (рис. 97-4, а),

положительным и отрицательным (рис. 97-4, б) и двумя отрицательными (рис. 97-4, в).

Рис. 97-4

98. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. НЕОДНОРОДНЫЕ И ОДНОРОДНЫЕ ЭЛЕКТРИЧЕСКИЕ ПОЛЯ

Электрическое поле невидимо, но иногда очень важно показать, как оно распределено в пространстве, например, вблизи антенны той или иной конфигурации, между обкладками конденсатора или между электродами электронно-лучевой трубки, и т. д. В этом случае его можно изобразить

графически с помощью линий вектора напряженности E , которые также называют силовыми линиями электрического поля.

Линией вектора напряженности или силовой линией электрического поля называют линию, в каждой точке которой вектор напряженности направлен по касательной к ней (рис. 97-1).

Электрическое поле можно было бы изобразить графически, показав в каждой его точке вектор напряженности, но поскольку все векторы прямые, то они пересекали бы друг друга и картина получилась бы крайне сложной. Поэтому выбрали такие линии, чтобы вектор напряженности к ним в каждой точке был направлен по касательной. Но если через каждую точку пространства, занятого электрическим полем, провести силовую линию, то

все они сольются. Чтобы этого не случилось и чтобы охарактеризовать величину напряженности поля в

данном месте, договорились густоту силовых линий выбирать такой, чтоб их количество при пересечении некоторой единичной площадки, перпендикулярной линиям, было равно напряженности поля в этом месте. Например, чтобы показать, что в данном месте напряженность поля равна 5 Н/Кл, можно через площадку в 1 см2, перпендикулярную линиям, провести 5 силовых линий, а там, где напряженность поля больше, провести их, соответственно, больше и тем самым охарактеризовать величину поля по их густоте.

При графическом изображении электрических полей с помощью силовых линий надо руководствоваться следующими правилами:

а) линии вектора напряженности электрического поля (силовые линии) начинаются и оканчиваются на электрических зарядах или уходят в бесконечность, т. е. они всегда разомкнуты и внутрь проводников с неподвижными зарядами не проникают;

б) движущиеся электрические заряды и переменны магнитные поля связаны с вихревыми электрическим полями, силовые линии которых замкнуты;

в) линии вектора напряженности электростатического поля (силовые линии) выходят из положительных зарядов и входят в отрицательные или уходят в бесконечность от положительных зарядов, или входят из бесконечности в отрицательные заряды;

г) линии вектора напряженности электрического поля (силовые линии) никогда не пересекаются, так как их пересечение означало бы наличие в точке пересечения двух различных направлений одного и того же вектора напряженности, направленного по касательной к ним, что не имеет смысла;

д) чем гуще располагаются линии вектора напряженности (силовые линии), тем больше напряженность поля в этом месте; при этом силовые линии не могут сливаться, так как это означало бы бесконечно большую величину напряженности поля.

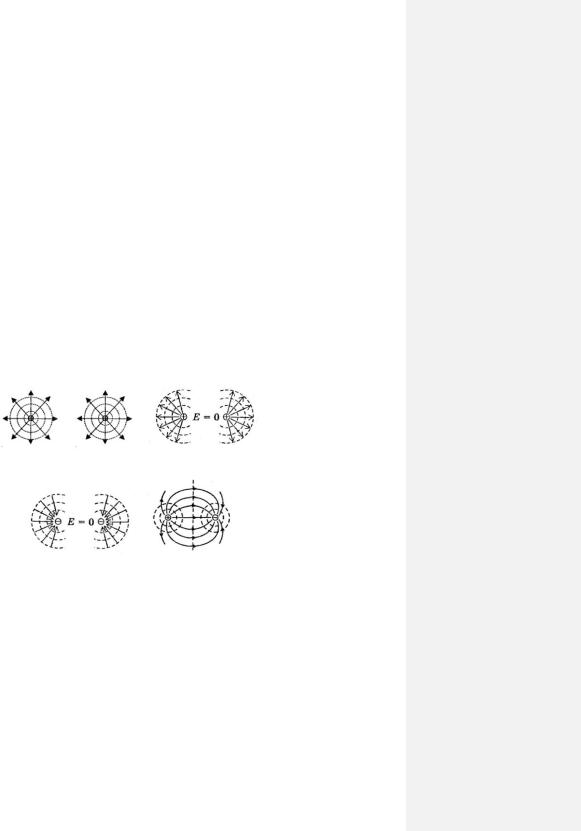
На рис. 98-2 – 98-6 изображена плоская картина распределения линий вектора напряженности (силовых линий) электрических полей вблизи точечных зарядов-источников.

Рис. 98-5 Рис. 98-6

Здесь сплошными линиями изображены линии вектора напряженности (силовые линии), а штриховыми – эквипотенциальные линии, о которых мы будем говорить в п. 105.

Следует отметить, что, когда расстояние r в формуле напряженности (97.2) или (97.3) от точки поля до заряда-источника равно нулю, напряженность становится неопределенной величиной, ведь на ноль делить нельзя. Следовательно, точка, соответствующая r = 0, является особой точкой поля. Линии вектора напряженности (силовые линии) могут сколь угодно близко подходить к этой точке, но не должны приблизиться к заряду вплотную, так как при r = 0 их густота становится неопределенной. Поэтому правильнее было бы не доводить их до зарядов-источников вплотную.

В случае уединенных точечных зарядов вблизи них (рис. 98-2 и 98-3) силовые линии прямые и радиально расходящиеся от зарядов (из положительного выходят, а в отрицательный входят). Электрическое поле вокруг таких зарядов обладает центральной симметрией.

Силовые линии вблизи двух одноименных зарядов (рис. 98-4 и 98-5) искривлены и лишь вдали от них асимптоматически приближаются к прямой линии. В точке посередине между такими зарядами напряженность поля равна нулю и силовые линии здесь отсутствуют.

Электрическое поле двух разноименных точечных зарядах (рис. 98-6) является осесимметричным относительно прямой силовой линии, проходящей через эти заряды. Чем ближе к оси симметрии, тем гуще располагаются силовые линии, т. е. тем больше здесь напряженность электрического поля.

Поля, изображенные на рис. 98-2-98-6 служат примером неоднородных полей, т. е. полей с переменной от точки к точке напряженностью. Такие поля изображаются или кривыми силовыми линиями, или непараллельными прямыми, или, наконец, параллельными прямыми, но расположенными с разной густотой. Следовательно, поля точечных зарядов это неоднородные поля.

Поле, в каждой точке которого вектор напряженности остается постоянным по величине и направлению, называется однородным.

Линии вектора напряженности (силовые линии) однородного электрического поля представляют собой параллельные прямые, распределенные по пространству с одинаковой густотой, т. е. отстоящие друг от друга на равных расстояниях.

Примером однородного поля является поле бесконечной равномерно заряженной плоской поверхности (рис. 98-7). Кроме того, однородным является поле между двумя разноименно заряженными бесконечными плоскими поверхностями с равномерным распределением и одинаковой поверхностной плотностью зарядов на них (рис. 98-8). Каждая такая поверхность создает с обеих сторон свое поле. При этом силовые линии обоих полей между поверхностями сонаправлены, поэтому результирующая напряженность вдвое больше напряженности поля каждой поверхности. Позади же поверхностей силовые линии их полей антинаправлены. А так как напряженности полей, созданных каждой поверхностью, равны по модулю друг другу, то результирующие напряженности там равны нулю.

Поле плоского конденсатора, обкладки которого заряжены разноименно, можно считать однородным, если расстояние между обкладками во много раз меньше их линейных размеров. У границ обкладок конденсатора однородность поля нарушается и силовые линии искривляются (рис. 98-9).

Картина распределения силовых линий, изображенная на этих рисунках верна только тогда, когда заряды-источники полей находятся в вакууме или в однородном и изотропном диэлектрике. В неоднородной или неизотропной среде, где относительная диэлектрическая проницаемость меняется от точки к точке, картина распределения силовых линий будет выглядеть значительно сложнее.

Если в какую-либо точку поля поместить заряженное тело или частицу, то под действием кулоновой силы это тело или частица будут двигаться с ускорением, направленным по касательной к силовой линии. Если силовая линия прямая и вектор скорости тела или частицы направлен вдоль силовой линии, то тело или частица будут двигаться прямолинейно вдоль нее.

99. ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Спомощью формулы (97.2) или (97.3) мы можем определить напряженность поля точечного заряда,

априменяя принцип суперпозиции, – и напряженность поля системы точечных зарядов. Чтобы определить напряженность поля протяженных зарядов (напряженность поля заряженной нити или

плоскости), введем величину потока вектора напряженности ФЕ .

Пусть линии вектора напряженности однородного электрического поля пересекают некоторую площадку S , расположенную перпендикулярно этим линиям (рис. 99-1, а). Потоком вектора напряженности ФЕ через площадку называют скалярную величину, равную произведению модуля

вектора напряженности и величины этой площадки

ФЕ ES

Если площадка расположена параллельно линиям вектора напряженности, то, очевидно, что они ее не пересекают (рис. 99-1, б), поэтому поток вектора напряженности через такую площадку равен нулю.

Пусть линии вектора E образуют угол с нормалью n к площадке S . Разложим вектор E на нормальную En и тангенциальную (т. е. касательную) Et , составляющие по отношению к площадке S

напряженности электрического поля сквозь некоторую площадку равен произведению модуля напряженности на величину площадки и на косинус угла между вектором напряженности и нормалью к этой площадке. Поскольку косинус угла может быть как положительным, так и отрицательным, поток

вектора E тоже может быть как больше, так и меньше нуля, следовательно, поток вектора напряженности электрического поля – величина алгебраическая, он может быть как положителен, так и

отрицателен. Условно считают, что поток положителен, когда линии вектора E выходят из площадки S (рис. 99-2, а), и отрицателен, когда они входят в эту площадку (рис. 99-2, б).

Поскольку количество линий вектора E через единичную площадку равно модулю вектора напряженности в этом месте, то произведение ES равно числу линий через всю площадку S :

ФЕ ES NE ,

где NE – число линий вектора напряженности через площадку S .

Физический смысл ФЕ : поток вектора напряженности электрического поля числено равен количеству линий вектора напряженности через площадку, которую эти линии пересекают.

поверхность отрицательный, а на выходе – такой же по модулю, но положительный. Значит, поток вектора напряженности сквозь замкнутую поверхность, не содержащую зарядов, равен нулю.

100. ТЕОРЕМА ГАУССА

Окружим некоторый точечный заряд-источник qист электрического поля замкнутой сферической

Получается, что поток вектора напряженности точечного заряда-источника сквозь замкнутую поверхность не зависит от того, на каком расстоянии находится эта поверхность от заряда, ведь в формулу (100.1) не входит это расстояние. В общем случае заряд может располагаться не только в центре, а в любой точке внутри замкнутой сферической поверхности, да и сама замкнутая поверхность может быть не только сферической, а любой произвольной формы (рис. 100-2). Очевидно, что

количество линий вектора E , пересекающих такую поверхность, останется прежним, поскольку согласно (100.1) оно зависит только от величины заряда-источника и от диэлектрических свойств окружающей среды.

Если внутри замкнутой поверхности будет не один, а N зарядов, то очевидно, что поток вектора напряженности, созданный всеми зарядами, будет равен алгебраической сумме потоков, созданных каждым точечным зарядом в отдельности, от 1-го до N -го:

Выражение (100.2) называют теоремой Гаусса для потока вектора напряженности электрического поля в честь немецкого физика, который ее вывел.

Теорема Гаусса: поток вектора напряженности сквозь замкнутую поверхность прямо пропорционален алгебраической сумме электрических зарядов, расположенных внутри этой поверхности.

Из этой теоремы следует, что, если внутри замкнутой поверхности заряды есть, но их алгебраическая сумма равна нулю, то поток вектора напряженности сквозь эту поверхность, как и в случае отсутствия внутри нее зарядов, равен нулю.

101. ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА К РАСЧЕТУ НАПРЯЖЕННОСТИ ПОЛЯ ПРОТЯЖЕННЫХ ЗАРЯДОВ

А. Поле бесконечной равномерно заряженной плоскости

плоскости составляющие (рис. 101-1, б). Все тангенциальные составляющие Et опять же скомпенсируют

друг друга, а останутся только сонаправленные нормальные составляющие En .

В результате силовые линии поля уединенной бесконечной плоскости, заряженной положительно, будут представлять собой параллельные прямые, направленные от плоскости перпендикулярно к ней и уходящие в бесконечность (рис. 101-2, а), а силовые линии поля уединенной плоскости, заряженной отрицательно, будут представлять собой параллельные прямые, направленные из бесконечности перпендикулярно к плоскости (рис. 101-2, б). Эти прямые линии будут располагаться на одинаковом расстоянии друг от друга так, как при равномерном распределении зарядов на плоскости E const .

Таким образом, поле бесконечной равномерно заряженной плоскости, является однородным.

Определим напряженность электрического поля, создаваемого такой плоскостью, используя теорему Гаусса. Для этого мысленно окружим некоторый участок плоскости площадью S, на котором сосредоточен заряд q, замкнутой цилиндрической поверхностью (ведь такая поверхность может быть любой формы), ориентированной так, чтобы образующие цилиндра были перпендикулярны плоскости, а его основания параллельны ей (рис. 101-2, в).

вектора напряженности сквозь его боковую поверхность равен нулю. Весь поток идет сквозь оба

цилиндрической поверхностью (напомним, что форма поверхности никакого значения не имеет, лишь бы она была замкнутой. Мы ее выбрали цилиндрической исключительно для удобства доказательства):

Е 0

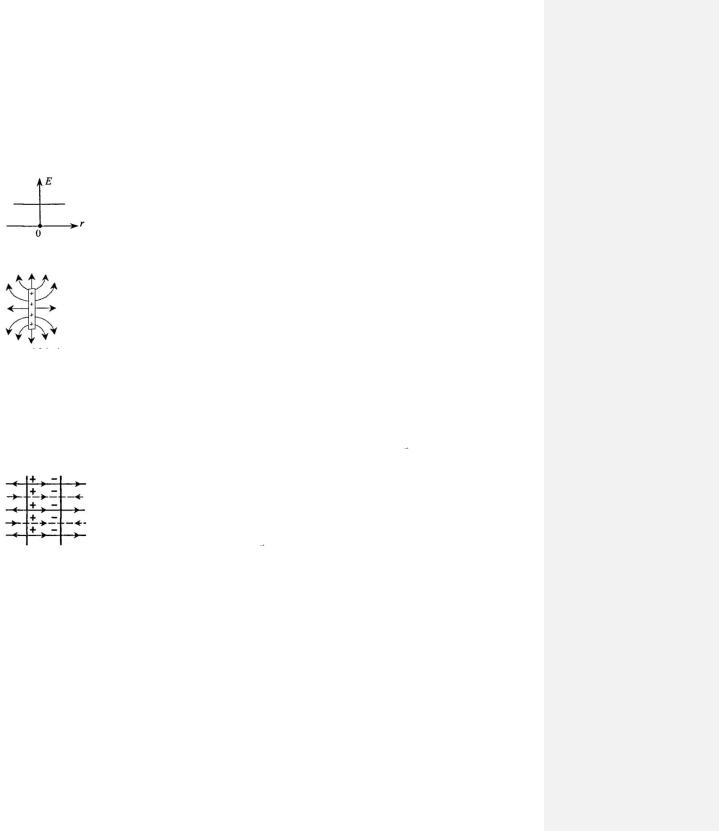
где из определения поверхностной плотности заряда

Б. Поле двух бесконечных, равномерно разноименно заряженных плоскостей, расположенных параллельно друг другу

Рассмотрим поле, образованное двумя бесконечными, равномерно заряженными плоскостями, расположенными праллельно друг другу. Пусть левая плоскость заряжена положительно, а правая – отрицательно, причем поверхностные плотности зарядов на обеих плоскостях равны друг другу. Поле

положительно заряженной плоскости изобразим сплошными линиями вектора E , а поле отрицательно заряженной плоскости – штриховыми линиями (рис. 101-5). Из рис. 101-5

видно, что вне пространства между плоскостями векторы напряженностей полей положительной и отрицательной плоскостей антинаправлены друг другу. Но так как они по модулю одинаковы, то друг друга компенсируют, в результате чего слева от положительной плоскости и справа от отрицательной результирующая напряженность равна нулю, я электрического поля нет. Вместе с тем в прове между

плоскостями линии вектооа E срнаправлены, поэтому там напряженности полей, создаваемых каждой плоскостью суммируются.

Поскольку поверхностные плотности зарядов на плоскостях одинаковы и располагаются они в одной и той же среде, то напряженность результирующего поля E равна удвоенной напряженности поля, создаваемого каждой плоскостью в отдельности, E1 :

Формула (101.5) позволяет определить напряженность электрического поля, созданного двумя параллельными, бесконечными разноименно заряженными плоскостями в пространстве между ними. Их этой формулы следует, что напряженность такого поля в каждой точке одинакова, так как она не зависит от расстояния от точки до плоскостей. Таким образом, поле таких плоскостей однородно и целиком

сосредоточено между ними.

График E E r , где r – расстояние от точки поля с напряженностью E до плоскости, показан на рис. 101-6. Здесь d – расстояние между плоскостями.

Поле в пространстве между антеннами или обкладками конечных размеров, заряженными разноименно (поле плоского конденсатора), показано на рис. 98-9. Поскольку тангенциальные направления векторов напряженности, создаваемых зарядами на краях таких антенн и обкладок, уже компенсируются, вблизи краев имеют место отклонения от однородности тем большие, чем ближе к концу пластины.

В. Поле бесконечной, равномерно заряженной цилиндрической поверхности

Пусть электрическое поле создано бесконечной длинной цилиндрической поверхностью радиусом R, заряженной равномерно, с линейной плотностью зарядов . Если этот цилиндр заряжен положительно, то из соображений симметрии следует, что линии вектора напряженности будут радиально расходиться от него так, что их густота на одном и том же расстоянии от цилиндра будет со всех сторон одинакова. Эти линии будут параллельными друг другу прямыми (рис. 101-7), однако однородным поле не будет, так как по мере удаления от цилиндра густота линий

вектора E будет убывать, значит, и величина напряженности электрического поля будет уменьшаться, поскольку некоторую единичную площадку по мере

удаления от цилиндра будет пересекать все меньшее и меньшее число линий.

Определим напряженность электрического поля, созданного этим бесконечно длинным цилиндром, в некоторой точке, удаленной на расстояние r от его осевой линии mn . Для этого охватим заряд q , сосредоточенный на некотором участке цилиндра длиной l , замкнутой и тоже цилиндрической поверхностью с радиусом основания r и высотой l . При этом образующие этой цилиндрической поверхности должны быть параллельны цилиндру, а основания – перпендикулярны ему. Определим

поток вектора E сквозь эту замкнутую цилиндрическую поверхность. Очевидно, что линии вектора E пересекают только ее боковую поверхность, а по основаниям лишь скользят, не пересекая их. Поэтому

весь поток вектора E проходит только сквозь боковую поверхность внешнего цилиндра высотой l . При этом количество линий, пересекающих каждую единицу площади этой боковой поверхности, одинаково,

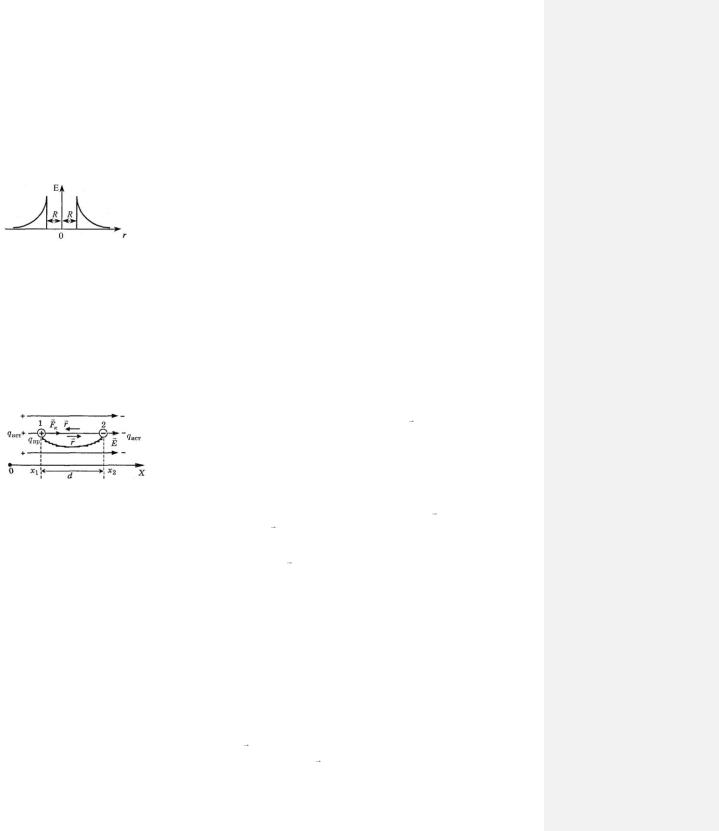
Напомним, что – заряд, охватываемый замкнутой цилиндрической поверхностью высотой / и радиусом основания г.

Подставим (101.7) в (101.6), а (101.9) в (101.8) и приравняем правые части получившихся выражений:

(нити) на расстоянии r R от его оси, где R – радиус цилиндра. Мы видим, что напряженность поля такого цилиндра обратно пропорциональна расстоянию до него.

имеет вид, изображенный на рис. 101-4, и обладает осевой симметрией в пространстве, окружающем антенну. Формула (101.10) применима к точкам, расположенным на расстоянии r , малом по сравнению с длиной стержня, и удаленным от его краев.

102. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ПОТЕНЦИАЛЬНЫЙ ХАРАКТЕР ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Найдем работу перемещения пробного положительного заряда, совершаемую в однородном электростатическом поле, силовые линии которого направлены слева от положительных зарядовисточников направо к отрицательным зарядам-источникам (рис. 102-1).

Пусть пробный заряд qпр перемещается из точки 1 в точку 2 по

силовой линии под действием силы Кулона F , которая действует на заряд слева направо, поскольку пробный заряд отталкивается от положительных зарядов-источников поля и притягивается к отрицательным зарядам-источникам. Пусть координата точки 1 на оси

координат OX будет x1 , а координата точки 2 – x2 . Поскольку сила,

Рис. 102-1

действующая на заряд qпр , сонаправлена с перемещением этого заряда из точки 1 в точку 2, то угол а между вектором этой силы и вектором перемещения r равен нулю. Тогда работа перемещения заряда qпр под действием силы F равна:

A Fd cos Fd .

Здесь d x2 x1 – модуль вектора перемещения r , равный проекции вектора перемещения на силовую линию, cos cos 0 1 .

Работа перемещения заряда, совершаемая силами Кулона в однородном электростатическом поле,равна произведению этого заряда, напряженности поля и проекции вектора перемещения на силовую линию.

Переместим теперь этот же заряд между теми же точками 1 и 2, но не вдоль силовой линии, а по некоторой кривой траектории (рис. 102-1). Любую кривую можно представить в виде ломаной линии с бесконечно большим числом сколь угодно малых ступенек. Работа перемещения заряда qпр вдоль

вертикальных участков этих ступенек будет равна нулю, так как при этом вектор перемещения будет перпендикулярен вектору электрической силы F , поскольку ее направление останется прежним. Значит, угол а между направлениями векторов перемещения и силы F , станет равен 90°, а косинус такого угла,