
Стеграммы лекций 6-10 и 13
.pdf
подробно разберем возможные варианты сравнения фактического и ожидаемого, чтобы продемонстрировать имеющиеся «подводные камни».
Рассмотрим следующую последовательность задач.
1.Определение достоверности отличия выборочной дисперсии от ожидаемого значения.
2.Определение доверительных границ к выборочной дисперсии.
3.Определение достоверности различия двух выборочных дисперсий.
Задача 10.1. Пусть по имеющимся литературным данным (обычно такая фраза должна означать, что количество наблюдений в «литературных данных» во много раз больше, чем в собственных, поэтому их статистическая погрешность много меньше и ею можно пренебречь; однако на практике она встречается тогда, когда в литературном источнике данные описаны недостаточно подробно, чтобы можно было рассчитать их статистическую достоверность, или автор не знает, как это сделать)
среднеквадратичное отклонение роста студентов 1-го курса равно 8,5 см, а полученное по 15 наблюдениям студентов 341 группы значение равно 5,6 см. Может ли такое различие быть случайным?
При стандартной несмещенной оценке дисперсии S x1 x 2 ... xn x 2 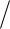 n 1
n 1
рассчитывается сумма квадратов отклонения от среднего арифметического. Если предположить, что наблюдаемая случайная величина распределена нормально с
дисперсией D и математическим ожиданием M, то x M 2 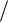 D – квадрат нормально распределенной случайной величины с нулевым математическим ожиданием и единичной
D – квадрат нормально распределенной случайной величины с нулевым математическим ожиданием и единичной
дисперсией, т.е. |
имеет распределение |
«хи-квадрат» |
с одной степенью |
свободы 2 . |
|
|
|
|
|
|
1 |
Соответственно, |
вся оценка S имеет |
распределение |
D n 1 2 |
, где |
одна степень |
|
|
|
n 1 |
|
|
свободы пропала из-за взаимозависимости выборочного среднего и выборочной дисперсии.
В данном случае ожидаемая дисперсия D 8,52 72, 25 , а полученное значение
составило 5, 62 31,36 . Следовательно, |
72, 25 14 |
31,36 , откуда |
|
6, 08 . |
|
14 |
|
14 |
|
Вероятность того, что распределенная как 2 |
случайная величина принимает значение в |
|||
14 |
|
|
|
|
6,08 или более, можно рассчитать при помощи встроенной в Excel функции ХИ2РАСП:
ХИ 2РАСП 6,08;14 0,9644 . Следовательно, |
с вероятностью p 1 0,9644 0, 0356 |
|
распределенная как 2 |
случайная величина |
принимает значение в 6,08 или менее, |
14 |
|
|
поэтому с односторонней доверительной вероятностью p 0, 0356 различия в дисперсии достоверны.
Задача 10.2. В условиях предыдущей задачи определить доверительные границы для полученной оценки дисперсии с p=0,05.
В Excel есть встроенная функция ХИ2ОБР, для заданного p рассчитывающая такое значение x, что вероятность распределенной как 2 случайной величине принять значение, больше либо равное x, равна p. Если двусторонняя доверительная вероятность по условию равна 0,05, то односторонние равны 0,025 и тогда ХИ 2ОБР 0,025;14 26,12
и ХИ 2ОБР 0,975;14 5,63. Следовательно, с вероятностью 95% 2 -распределение с 14 степенями свободы находится в пределах от 5,63 до 26,12. Так как фактическая оценка дисперсии составила 31,36, то ее доверительные границы с p=0,05 – от 31,36 5, 63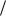 14 до 31,36 26,12
14 до 31,36 26,12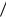 14 , или от 12,61 до 58,51. Доверительные границы к среднеквадратичному отклонению (нужно извлечь квадратный корень) – от 3,55 до 7,65.
14 , или от 12,61 до 58,51. Доверительные границы к среднеквадратичному отклонению (нужно извлечь квадратный корень) – от 3,55 до 7,65.
Обратите внимание, что доверительные границы к среднеквадратичному отклонению получились практически симметричными относительно среднего – это следствие достаточно большого количества наблюдений. Для меньшего количества наблюдений будет выраженная асимметрия доверительных границ, и записать 5, 6 2,1 будет уже нельзя.
Обратите также внимание, что ожидаемое среднее по курсу находится за пределами 0,95-доверительного интервала, т.е. различия дисперсий являются достоверными как минимум с p=0,05 (точное значение было вычислено в задаче 10.1).
Задача 10.3. Пусть в условиях задачи 1 также известно, что величина среднеквадратичного отклонения роста студентов 1-го курса рассчитана по 44 наблюдениям. Определить достоверность различия двух выборочных дисперсий.
Две полученные величины среднеквадратичного отклонения – 5,6 и 8,5 см, т.е. отношение дисперсий равно 5, 6 8,5 2 0, 4341.
8,5 2 0, 4341.
Так как стандартная оценка дисперсии нормальной случайной величины распределена как n2 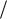 n , где n – число степеней свободы, т.е. на единицу меньше
n , где n – число степеней свободы, т.е. на единицу меньше
количества наблюдений, то отношение двух оценок из нормально распределенных случайных величин с одинаковой дисперсией имеет распределение Фишера–Снедекора (см. лекцию №6), в данном случае с 14 и 43 степенями свободы. Для расчета функции распределения такой случайной величины в Excel имеется встроенная функция FРАСП, а
так как |
FРАСП 0, 4341;14;43 0,9539 , |
то с |
доверительной |
вероятностью |
|
p 1 0,9539 0, 0461 среднеквадратичное |
отклонение |
роста студентов в 341 группе |
|||
достоверно меньше, чем в целом по курсу. |
|
|
|
||
При |
определении |
достоверности |
различий |
дисперсий |
использовалось |
предположение о нормальности наблюдаемой случайной величины, так как только в этом случае оценки дисперсий и их отношения есть 2 -распределение и распределение Фишера–Снедекора. Понятно, что реально наблюдаемые случайные величины не будут нормальными. Поэтому для применимости используемой техники нужно, чтобы распределение оценки практически не зависело от формы распределения исходной случайной величины, т.е. центральная предельная теорема выполнялась с достаточной
точностью. Используемые в примерах объемы наблюдений в 15 и 44 позволяют приближенно считать полученные достоверности различия дисперсий достаточно точными в том случае, если распределение роста студентов достаточно «приличное». Несмещенная оценка выборочного коэффициента эксцентриситета дает значение 3,68, что дает право сомневаться в полученных результатах, поскольку применимость ЦПТ при оценке дисперсии предъявляет более жесткие требования к форме распределения, чем при проверке достоверности различия средних арифметических.
Определение достоверности различия средних Критерий Стьюдента
Часто приходится сравнивать собственные данные с литературными и делать вывод о достоверности или недостоверности их различий. Разберем возможные варианты сравнения:
1.Сравнение выборочного среднего с точно известным значением, если известна дисперсия.
2.Сравнение выборочного среднего с точно известным значением, если дисперсия неизвестна.
3.Сравнение двух выборочных средних, если известна дисперсия.
4.Сравнение двух выборочных средних, если дисперсии равны, но неизвестны.
5.Сравнение двух выборочных средних в группах одинакового размера.
6.Сравнение двух выборочных средних в группах разного размера.
Задача 10.4. Пусть по литературным данным, основанным на большом количестве наблюдений, средний арифметический рост студентов 1-го курса равен 172,7 см при среднеквадратичном отклонении 8,5. В 341 группе 15 студентов со средним ростом 175,1 см. Определить достоверность различий средних.
В качестве первого шага нужно рассчитать коэффициент эксцесса для распределения студентов по росту. Пусть мы это сделали и получили значение 3,68 и посчитали его достаточно малым для корректности применения ЦПТ. Этот шаг необходим для всех приводимых ниже задач, далее приводить его мы не будем.
Если бы распределение роста студентов имело математическое ожидание 172,7 и среднеквадратичное отклонение 8,5, то среднее арифметическое из 15 наблюдений имело
бы |
математическое |
ожидание |
172,7 |
и |
среднеквадратичное |
|
отклонение |
|||||
x 8,5 |
|
|
|
|
|
|
|
|||||
15 2, 2 . |
Наблюдаемое |
среднее арифметическое |
составило |
175,1, что на |
||||||||
175,1 172, 7 2, 4 |
см |
больше |
ожидаемого. |
Вычислим |
величину |
|||||||
t x M 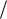 2, 4
2, 4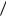 2, 2 1,09 . В том случае, когда выполняется нулевая гипотеза о том,
2, 2 1,09 . В том случае, когда выполняется нулевая гипотеза о том,
что наблюдаемая случайная величина имеет M 172, 7 и среднеквадратичное отклонение 8,5, сконструированная таким образом величина t имеет нулевое среднее и единичную дисперсию. Для расчета вероятности таких уклонений нормально распределенной

случайной |
величины |
в |
Excel |
есть |
функция |
НОРМСТРАСП: |
НОРМСТРАСП 1,09 0,8623 , т.е. |
вероятность принять значение 1,09 или больше |
|||||
примерно |
равна 1 0,8623 0,1377 . |
Следовательно, |
нулевая гипотеза о том, что |
|||
наблюдаемая случайная величина имеет математическое ожидание 172,7 и среднеквадратичное отклонение 8,5 должна быть отвергнута с односторонней доверительной вероятностью p 0,1377 или двусторонней доверительной вероятностью p 0, 2753. При таких величинах доверительных вероятностей говорить о достоверных различиях некорректно.
Приведенный пример относился к случаю, когда в нулевой гипотезе были представлены ожидаемые величины и математического ожидания, и дисперсии наблюдаемой случайной величины. Чаще встречается другой случай, когда нужно сравнить с ожидаемым значением выборочное среднее из случайной величины, среднеквадратичное отклонение которой также неизвестно. В этом случае опять конструируем величину t x M 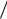 s x , где – оценка ожидаемого
s x , где – оценка ожидаемого
среднеквадратичного отклонения. Так как стандартная оценка среднеквадратичного отклонения s x распределена как k2 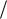 k , то в предположении об истинности нулевой
k , то в предположении об истинности нулевой
гипотезы случайная величина t распределена по Стьюденту (см. лекцию №6) с k степенями свободы, где k – на единицу меньше количества наблюдений. Критерий Стьюдента часто также называют Т-критерием.
Задача 10.5. Пусть средний рост 15 студентов 341 группы равен 175,1 см с выборочным среднеквадратичным отклонением 5,6 см. Достоверно ли это различие со средним ростом по курсу, равным 172,7 см?
Аналогично |
|
предыдущей |
задаче |
рассчитываем |
статистику |
||
t 175,1 172, 7 |
5, 6 |
|
|
2, 4 1, 45 1, 66 . При помощи встроенной в Excel функции |
|||
15 |
|||||||
СТЬЮДРАСП |
получаем |
значение |
доверительной |
вероятности |
|||
СТЬЮДРАСП 1,66;14;2 0,1191 , то есть полученное выборочное среднее достоверно отличается от тестового значения с двусторонней доверительной вероятностью p 0,1191
Задача 10.6. Средний рост 15 и 13 студентов 341 и 343 групп равны 175,1 см и 167,2 см соответственно, причем среднеквадратичная погрешность метода определения роста составила 8,5 см. Достоверны ли различия средних?
Так как различие в среднем росте студентов разных групп близко к разбросу роста студентов на курсе, можно попробовать этим различием пренебречь и проверить предположение о том, что оба полученных средних – результат наблюдения случайных величин с совпадающим средним и среднеквадратичным отклонением, равным 8,5.
Пусть xk – набор значений в первой группе из n наблюдений, а yk – набор значений во второй группе из m наблюдений, x и y – средние арифметические соответственно в первой и второй группе. Рассмотрим случайную величину x y .
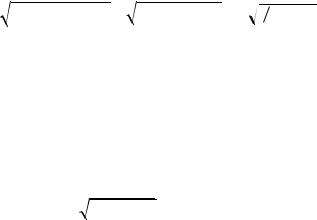
Тогда, так как x и y – средние арифметические из одной случайной величины, то их математические ожидания совпадают, отчего математическое ожидание равно нулю, а дисперсия равна сумме дисперсий:
x y 
 2 x 2 y
2 x 2 y 
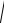 2
2 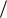 n 2
n 2 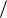 m
m 
 1 n 1
1 n 1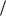 m
m
Так как x и y – средние из (предположительно) достаточно большого количества наблюдений, то (после соответствующей проверки) их можно считать распределенными примерно нормально, следовательно и x y можно также считать нормально распределенной.
В результате получили, что при условии истинности нулевой гипотезы разность средних распределена нормально с нулевым математическим ожиданием и
среднеквадратичным отклонением 8,5
 1
1 15 1
15 1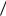 13 3, 22 . Так как наблюдаемая разность средних оказалась равной 175,1–167,2=7,9, то t 7,9
13 3, 22 . Так как наблюдаемая разность средних оказалась равной 175,1–167,2=7,9, то t 7,9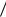 3, 22 2, 45. Сконструированная величина t при истинности нулевой гипотезы распределена нормально с нулевым средним
3, 22 2, 45. Сконструированная величина t при истинности нулевой гипотезы распределена нормально с нулевым средним
и единичной дисперсией, поэтому с односторонней |
доверительной вероятностью |
p 1 НОРМСТРАСП 2, 45 1 0,9929 0,0071 среднее |
в 341 группе достоверно |
больше среднего во второй группе. |
|
Достоверность различий рассчитывалась в предположении о том, что разница математических ожиданий много меньше фактического разброса по курсу и ею можно пренебречь. Если это предположение неверно, то достоверность различий окажется меньше (см. следующую задачу).
Задача 10.7. Средний рост студентов в 341 группе равен 175,1 см с выборочным среднеквадратичным отклонением 5,6 см, а в 343 группе – 167,2 см с выборочным среднеквадратичным отклонением 10,3 см. Значимы ли эти различия?
В качестве нулевой гипотезы примем, что математические ожидания и среднеквадратичные отклонения в обеих группах совпадают.
Для начала нужно получить согласованную оценку дисперсии в предположении об истинности нулевой гипотезы. В 341 группе оценка дисперсии равна 5, 62 31,36 , а в 343
– 10,32 106, 09 . Если бы размеры групп были одинаковы, то в качестве согласованной оценки дисперсии по обеим группам нужно было бы брать их полусумму, но так как первая группа больше, то ее нужно брать с большим весом. Поскольку при несмещенной оценке выборочной дисперсии сумма квадратов отклонений делится на n 1, то при объединении наборов из n и m наблюдений их оценки дисперсии нужно объединять с
весами |
n 1 |
и |
m 1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
n m 2 |
n m 2 |
|
|
|
|
|
|||
|
|
|
31,36 |
|
15 1 |
106, 09 |
13 1 |
65,85 , |
|
|
|
|
|
|
|
||||
|
|
|
15 13 2 |
15 13 2 |
|||||

|
|
|
|
|
|
||
откуда согласованная оценка |
среднеквадратичного отклонения |
65,85 8,1. |
Далее |
||||
|
|
|
x y 8,1 |
|
3,1 |
|
|
аналогично |
предыдущей |
задаче |
1 15 1 13 |
и |
|||
t175,1 167, 2  3,1 2,55.
3,1 2,55.
Вданном варианте расчета разность средних делится не на заранее известную величину среднеквадратичного отклонения, а на ее оценку, полученную по набору наблюдений, следовательно, полученная величина распределена не нормально, а по Стьюденту. Так как оценка дисперсии была получена объединением двух оценок с количеством степеней свободы 14 и 12, то общее количество степеней свободы равно
14+12=26. Так как СТЬЮДРАСП 2,55;26;2 0,017 , то различия достоверны с p 0, 017 и нулевая гипотеза отвергается.
Обратите внимание, что в этом случае доверительная вероятность (т.е. вероятность ошибиться, приняв нулевую гипотезу за истину) p 0, 017 выше, чем в предыдущей задаче 6, где p 0, 0071. Также следует обратить внимание на то, что отвергнув в задаче 7 нулевую гипотезу, нельзя говорить о достоверном различии средних, поскольку в нулевой гипотезе утверждалось более сильное предположение – о том, что в сравниваемых группах совпадали и средние, и дисперсии. Поэтому при получении достоверных различий вывод более расплывчатый – что различаются или средние, или дисперсии, или оба параметра вместе.
Если требуется определить достоверность различий средних арифметических по группам безотносительно равенства или неравенства дисперсий, то схема расчета немного другая.
Задача 10.8. Пусть средний рост произвольно выбранных 10 студентов 341 группы равен 174,5 см с выборочным среднеквадратичным отклонением 6,5 см, а произвольно выбранных 10 студентов 343 группы – 171,2 с выборочным среднеквадратичным отклонением 4,3 см. Достоверны ли различия средних?
|
|
Пусть xk – результаты наблюдений в первой группе, а yk – во второй группе, |
x |
|||||||||||||||||||||||||
и y – их средние арифметические. Рассмотрим новые случайные величины k |
xk |
yk |
и |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
их среднее |
арифметическое |
. Тогда |
|
|
|
|
2 |
|
x |
|
2 |
|
|
y |
|
n , |
где |
n 10 |
– |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
количество наблюдений в каждой из групп. В нашем случае |
|
174,5 171, 2 3,3 , |
а |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
6,52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,32 10 2, 46 . |
Следовательно, |
|
t 3,3 2, 46 1,34 . |
Так |
как |
||||||||||||||||||||||
рассматривалась случайная величина – среднее арифметическое из 10 пар разностей ростов в первой и второй группе, то оценка дисперсии разности ростов имела 9 степеней свободы. Следовательно, полученная величина t при условии истинности нулевой гипотезы должна быть распределена по Стьюденту с 9 степенями свободы. Поскольку СТЬЮДРАСП 1,34;9;2 0, 2131 , то различия среднего арифметического в группах
недостоверны.

Чаще всего в условиях последней задачи нужно сравнивать средние величины в группах безотносительно дополнительных предположений о равенстве дисперсий или равенстве количеств наблюдений.
Задача 10.9. Пусть средний рост 15 студентов 341 группы равен 175,1 см с выборочным среднеквадратическим отклонением 5,6 см, а 13 студентов 343 группы – 167,2 см с выборочным среднеквадратическим отклонением 10,3 см. Достоверны ли различия средних в группах?
Пусть xk – результаты наблюдений в первой группе, а yk – во второй группе, x
и y – их средние арифметические. Рассмотрим случайную величину x y с нулевым математическим ожиданием в случае справедливости нулевой гипотезы. При определении
ее |
|
среднеквадратического |
|
|
|
отклонения |
имеем |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 2 y |
2 x |
n 2 y |
m , |
что |
в |
нашем |
случае |
дает |
|||||
|
|
|
|
175,1 167, 2 |
3, 2 2, 47 . |
|
|
||||||
5,62 15 10,32 13 3, 2 , |
откуда t |
После этого |
для |
||||||||||
определения достоверности различия нужно ответить только на один технический вопрос: какое количество степеней свободы для распределения Стьюдента нужно брать в этом случае?
Этот, казалось бы, мелкий технический вопрос в наиболее часто используемой схеме применения критерия Стьюдента вскрывает имеющиеся серьезные проблемы, поскольку сконструированная стандартным образом случайная величина t не распределена по Стьюденту. Исследование распределения t в этом случае – одна из центральных и до сих пор еще не решенных задач современной математической статистики.
С практической точки зрения эту техническую проблему обычно можно обойти. Для этого достаточно при определении достоверности различий рассчитать две вероятности – одну с количеством степеней свободы, на единицу меньше количества наблюдений в первой группе, а вторую – на единицу меньше количества наблюдений во второй группе. Истинная доверительная вероятность будет где-то между ними.
Если размеры групп достаточно велики, то полученные вероятности уже практически не зависят от количества степеней свободы, и распределение Стьюдента стремится к нормальному. Поэтому при сравнении среднего арифметического из достаточно больших групп эта техническая сложность малосущественна.
Если же размеры групп малы, то критерий Стьюдента справедлив только для заведомо нормально распределенных случайных величин. Однако в большинстве случаев анализируемая случайная величина не обязательно распределена нормально (или по малому объему наблюдений мы это доказать не можем), и тогда критерий Стьюдента, вообще говоря, неприменим.
Итак, в наиболее часто используемой схеме применения критерия Стьюдента им пользоваться нельзя, а в большинстве случаев, когда можно – он не нужен.
Расчет доверительных границ к математическому ожиданию
Практически во всех студенческих лабораторных работах присутствует фраза «данные представлены в виде M±m» безо всяких уточнений по поводу того, что такое M и m. И если в качестве M чаще всего приводится среднее арифметическое, то m в разных работах означает разные величины.
Для примера возьмем средний рост 44 студентов 1-го курса, равный 172,7 см с выборочным среднеквадратичным отклонением 8,5 см. В качестве претендентов на звание m могут выступать следующие величины:
1)x 8,5 , в этом случае m описывает характерный разброс роста студентов.
2)t x 2,02 8,5 17, 2 . Здесь коэффициент t подбирается таким образом,
чтобы 95% наблюдений (при условии, что наблюдаемая случайная величина распределена нормально) попадали в промежуток M±m, т.е. в 172,7±17,2. Сделать это можно при помощи встроенной функции Excel СТЬЮДРАСПОБР: СТЬЮДРАСПОБР 0, 05; 43 2, 02 . В этом случае m
задает интервал, в который попадает большая часть наблюдений.
3) x 8,5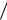

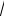 44 1,3, в этом случае m задает статистическую погрешность определения среднего.
44 1,3, в этом случае m задает статистическую погрешность определения среднего.
4) t x 2, 02 1,3 2, 6 . Здесь m определяет ширину доверительного
интервала для среднего арифметического, в котором с вероятностью 95% содержится математическое ожидание. Таким образом, с доверительной вероятностью p=0,05 математическое ожидание роста студентов находится в интервале 172,7±2,6 см.
Все четыре варианта представления результатов как M±m правомерны, однако в описании работы должно быть точно описано, какой именно вариант выбран автором.
Домашнее задание
Задача 10.10. Добросердечная буфетчица Антонина в гороховый суп кладет в среднем 15 сухариков со среднеквадратичным отклонением 3. В обед она налила студентам 23 тарелки горохового супа, куда насыпала в сумме 370 сухариков. Добрее ли буфетчица Антонина к студентам в обед?
Лекция №13 Корреляционный анализ
Анализ связи двух переменных Репрезентативные выборки Сложности интерпретации
Сегодняшняя лекция посвящена корреляционному анализу – набору статистических методов, позволяющих установить взаимосвязь между несколькими случайными величинами: изменения значений одних переменных сопровождается систематическими изменениями других. При помощи такой статистической обработки данных можно найти только очень слабый – статистический – тип связи между изучаемыми явлениями, по принципу «когда одно, тогда обычно и другое». Интерпретировать полученные связи как причинно-следственные нужно с предельной осторожностью, поскольку каждая полученная статистическая закономерность может быть объяснена целым рядом различных способов.
Первая проблема при интерпретации статистических связей как причинноследственных состоит в том, что мы можем найти статистическую связь с одним фактором, а истинной причиной является совсем другой фактор, с ним связанный, но в исследовании не учтенный.
Например, утверждается, что употребление в пищу свежих огурцов вредно для здоровья. Действительно, возьмем группу лиц, в течение длительного времени подвергавшуюся воздействию гипотетической вредности, т.е. в течение 70 лет и более употреблявших в пищу свежие огурцы. При обследовании группы выясняем, что большая часть этих людей уже умерла, а те, кто еще живы, плохо себя чувствуют. Следовательно, употребление свежих огурцов вредно для здоровья. Подвох здесь в том, что исследовалась заболеваемость и смертность в опытной группе из лиц старше 70 лет, а сравнивалась она не с заболеваемостью и смертностью в аналогичной возрастной группе, а со средними по всему населению данными.
Другой пример: если проверять на канцерогенность губную помаду, сравнивая заболеваемость раком между опытной группой лиц, использующих помаду, и контрольной группой лиц с тем же возрастным составом, получим, что губная помада – сильный канцероген, вызывающий рак шейки матки. Нетрудно догадаться, что причина этого вовсе не в канцерогенности помады, а в том, что мужчины значительно реже пользуются губной помадой и не болеют раком шейки матки из-за ее отсутствия.
К сожалению, сравнение опытной группы с населением в целом без выяснения сопоставимости возрастного и полового состава – нередкая ошибка даже в современных исследованиях. Например, в 1970-х годах в СССР было проведено исследование о связи артериальной гипертонии и курения. В результате было получено, что у курящих женщин среднее давление выше, чем у некурящих, а у мужчин связь обратная. Однако реальной
причиной полученного различия была сильная положительная связь возраста с артериальным давлением и разная возрастная структура курящих среди мужчин и женщин. У женщин курили в основном старшие возраста, начавшие курить еще в войну, а у мужчин больше курила молодежь.
Для избежания подобных ситуаций правильно использовать репрезентативные выборки – корректно сформированные сравниваемые группы, отличающиеся по исследуемому фактору и идентичные по всем остальным. Некорректное или тенденциозное (предвзятое, необъективное) формирование групп сравнения (нерепрезентативные выборки) влечет неверные выводы и является грубой ошибкой исследования.
Однако выделение по какому-то одному фактору обязательно влечет различия и по другим факторам, причем именно они могут быть причиной различий. Поэтому совершенно невозможно сформировать группы, которые по одному фактору различались бы, а по всем другим – нет. Поэтому важно понимать, что полностью репрезентативных выборок не существует.
Вторая причина сложности интерпретации статистических закономерностей как причинно-следственных в том, что очень легко перепутать причину и следствие.
Например, заболеваемость и смертность лиц, принимающих выписанные лекарства, достоверно выше, чем в контрольной группе с таким же половым, возрастным, профессиональным и т.д. составом. Тем не менее, не болезни являются следствием принимаемых лекарств, а наоборот.
В 1980-х годах при анализе заболеваемости кишечными инфекциями жителей города Шевченко была установлена достоверная положительная связь между заболеваемостью дизентерией Флекснера и номером квартиры. При попытке осмыслить данную связь сотрудникам санчасти удалось догадаться, что номер квартиры «сцеплен» с этажом. После перехода от номера квартиры к номеру этажа было получено, что на первом и пятом этажах заболеваемость различалась в три раза. Реальная причина этого оказалась простой: в городе не очень хорошо работал водопровод, из-за слабого напора вода на верхние этажи поступала не всегда, и жители верхних этажей в условиях жаркого климата запасали питьевую воду впрок.
Таким образом, на основании только статистических наблюдений выяснить, что является причиной, а что следствием, нельзя. Более того, возможна ситуация, когда одновременно наблюдаемые явления вообще не находятся в непосредственной причинноследственной связи.
Ковариация Определение коэффициента корреляции, его свойства
Линеаризация данных и зачем она нужна Недостатки коэффициента корреляции как меры линейности связи
На одной из прошлых лекций мы узнали, что измеряемые переменные можно условно разделить на три типа: номинальные, порядковые и измеряемые (nominal, ordinal,
