
Учебное пособие по дисциплине СиСПИ
.pdf
Ряд (1.3) точно определяет заданный сигнал s(t) в точках отсчета, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(n∆t). Можно доказать, что ряд (1.3) определяет функцию s(t) в любой момент t, а не только в точках отсчета t =n∆t. Воспользуемся для этого общими правилами разложения функции по ортогональной системе. В данном случае разложение производится по функциям вида (1.4), для которых интервал ортогональности равен бесконечности, а нор-
ма ||φn||:
|
|
|
|
sin |
2 |
|
|
(t n t) |
|
1 |
|
sin |
2 |
x |
|
|
|
|||||
|
2 |
|
|
|
2 |
m |
dt |
|
2 |
dx |
t . (1.6) |
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
(t n t) |
|
|
|
|
x |
|
|
|
|
||||||||
|
|
|
|
m |
|
|
m |
|
|
|
m |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Применим для определения значений коэффициентов ряда общую формулу, справедливую для обобщенного ряда Фурье:
(x) lim |
sin 2 x |
. |
(1.7) |
|
|||
|
x |
|
|
Сам обобщенный ряд Фурье представлен коэффициента-
ми:
c |
1 |
s(t) (t)dt . |
(1.8) |
||
t |
|||||
n |
|
n |
|
||
|
|
|
|||
При этом исходим из условия, что s(t) — квадратично интегрируемая функция (энергия сигнала конечна).
Для вычисления интеграла в выражении (1.8) воспользуемся формулой , согласно которой
|
1 |
|
1 |
m |
|
|
s(t) n (t)dt |
|
S( )ein t d . |
(1.9) |
|||
2Fm |
2 |
|||||
|
|
m |
|
20
Пределы интегрирования здесь приведены в соответствие
с заданной граничной частотой
|
m |
2 F |
|
m |
в спектре сигнала
s(0), а также в спектре функции φn(t).
Интеграл в правой части (1.9) с коэффициентом 1/2π есть не что иное, как значение s(t) в момент t = n∆t. Таким образом,
s(t) n (t)dt
ts(n t)
.
(1.10)
Подставляя этот результат в ное выражение
c |
n |
s(n t), |
|
|
(1.8), получаем окончатель-
(1.11)
из которого следует, что коэффициентами ряда (1.3) являются выборки функции s(t) в точках t = n∆t.
Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (1.3) сходится к функции s(t) при любом значении t.
Если взять интервал между выборками ∆t' меньшим, чем ∆t=1/2Fm, то ширина 2F'm спектра Ф'n(Ω) функции φ'n(t) будет больше, чем у спектра S(Ω) сигнала s(t) (рис. 1.8), но это не отразится на величине коэффициентов сп. Модуль функции Ф'n(Ω) изображен на рис.1.8 пунктиром.
При увеличении же ∆t'' по сравнению с ∆t спектр Ф''n(Ω) функции φ''n(t) (на рис. 1.8 показан штрих-пунктиром) становится уже, чем спектр сигнала s(t), и при вычислении интеграла в выражении (1.9) пределы интегрирования должны быть (-2πF''m, 2πF''m) вместо (-2πFm, 2πFm). Коэффициенты сn при этом являются уже выборками не заданного сигнала s(t), а некоторой другой функции s1(t), спектр которой ограничен наивысшей часто-
той F''m.
21

Итак, сокращение интервалов между выборками по срав-
нению с величиной 1/2Fm допустимо, но бесполезно. Увеличение же интервала сверх величины 1/2Fm недопустимо.
Рассмотрим теперь случай, когда длительность сигнала s(t) конечна и равна Т, а полоса частот по-прежнему равна Fm. Эти условия, строго говоря, несовместимы, так как функция конечной длительности обладает теоретически бесконечно широким спектром. Практически, однако, всегда можно определить наивысшую частоту спектра Fm так, чтобы «хвосты» функции времени, обусловленные отсеканием частот, превышающих Fm, содержали пренебрежимо малую долю энергии по сравнению с энергией заданного сигнала s(t). При таком допущении, если имеется сигнал длительностью Т с полосой частот Fm, общее число независимых параметров т. е. значений s(n∆t), которое необходимо для полного задания сигнала, очевидно, равно
N |
T |
1 2FmT 1, |
(1.12) |
|
t |
||||
|
|
|
при |
T |
1 |
можно считать N = 2FmT. При этом выражение (1.3) |
|||||||||
t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
принимает следующий вид: |
|
|
|
|
|
|
|
|||||
|
|
|
|
n F T |
sin |
|
(t n t) |
|
|
|||
|
|
|
|
m |
|
|
|
|||||
|
|
|
s(t) |
s(n t) |
|
|
|
m |
|
. |
(1.13) |
|
|
|
|
|
|
(t n t) |
|||||||
|
|
|
|
n F T |
m |
|
|
|||||
|
|
|
|
m |
|
|
|
|
|
|
||
Число N иногда называют числом степеней свободы сигнала s(t)
так как даже при произвольном выборе значений s(n∆t) сумма вида (1.13) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала. Число N иногда называют также базой сигнала.
В ряде случаев встречается необходимость представления сигнала с помощью частотных выборок спектральной функции S(Ω), а не временных выборок функции s(t). Для функции S(Ω) можно составить ряд, аналогичный выражению (1.3). Это не-
22

трудно сделать на основании взаимной заменимости переменных t и Ω в преобразованиях Фурье. Применительно к выражению (1.3) это означает, что t должно быть заменено на Ω, 2Ωm на Т, 2Fm на Т/2π; ∆t= 1/2Fт на ∆Ω = 2π /Т. Таким образом получается
|
F T |
|
|
|
|
|
|
sin |
T |
( n ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
m |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
S ( ) |
|
S (n ) |
|
|
|
|
|
|||||||||||
|
T |
|
||||||||||||||||
|
n FmT |
|
|
|
|
|
|
|
2 ( n ) |
(1.14) |
||||||||
|
|
|
|
T |
|
|
|
|
|
2 |
|
|
|
|||||
F T |
|
|
|
sin |
( n |
) |
|
|
||||||||||
|
2 |
|
2 |
|
|
|
|
|||||||||||
m |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||||
S (n |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
T |
|
T |
|
|
|
|
|
2 |
|
|
||||||||
n FmT |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 ( n T ) |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
Если ранее временной интервал между двумя соседними выборками должен был не превышать 2π/2Ωm,то теперь частотный интервал не должен превышать 2π/Т. При ширине спектра 2 Ωm, охватывающей область частот -Ωm < Ω < Ωm, число выборок
равно |
2 ь |
1 2F T 1, как и при представлении сигнала ря- |
|||
|
|||||
|
|
m |
|
|
|
|
|
|
|
|
|
дом (1). |
|
|
|
|
|
|
В общем случае выборки |
|
2 |
являются комплекс- |
|
|
S n |
|
|||
|
|
|
|
T |
|
ными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра — действительная и мнимая ча-
сти |
|
2 |
(или модуль и аргумент). Таким образом, общее |
|
S n |
|
|
||
|
|
T |
|
|
число параметров получается вдвое большим, чем при времен-
|
1 |
|
|
|
|
|
— дей- |
||
|
||||
ном представлении сигнала, когда выборки S n |
|
|
||
|
2Fm |
|
||
ствительные числа. Избыточность представления сигнала в ча-
23

стотной области легко устраняется, если учесть, что |
|
2 |
|||
S n |
|
||||
|
|
|
|
|
T |
|
n |
2 |
|
|
|
S |
|
являются комплексно-сопряженными числами, |
|||
|
|||||
|
|
T |
|
|
|
|
и |
|
|
|
|
так
что задание одной из них однозначно определяет другую. Таким образом, число независимых параметров или степеней свободы
сигнала равно
2FmT
1
, как и при представлении сигнала во
временной области.
Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временных выборок.
|
|
F T |
|
|
2 |
|
|
F T |
|
|
||
E |
m |
|
2 |
|
|
|
|
|
m |
2 |
|
|
|
|
|
|
|
|
, |
||||||
cn |
|
|
|
s(n t) |
||||||||
|
|
n F T |
|
|
|
|
m |
n F T |
|
|
||
|
|
|
m |
|
|
|
|
|
m |
|
|
|
|
|
|
E |
|
|
1 |
|
F T |
2 |
|
|
|
s |
(t) |
|
|
|
|
|
m |
s(n t) . |
|
|
||
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
2F T n F T |
|
|
|||||
|
|
|
|
|
|
m |
|
|
m |
|
|
|
(1.15)
(1.16)
Из последнего выражения видно, что средняя за время Т мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем отсчетным точкам, число которых равно 2FmТ.
1.2 Методы модуляции в системах связи
Для передачи информации на расстояние применяются сигналы, эффективно излучаемые с помощью антенных устройств и обладающие способностью распространяться в виде свободных радиоволн в среде, разделяющей отправителя и получателя информации. Такими сигналами являются высокочастотные колебания. Передаваемая информация должна быть тем или иным способом заложена в высокочастотное колебание, называемое несущим. Частота ω0 этого колебания выбирается в
24
зависимости от расстояния, на которое должна передаваться информация, от условий распространения радиоволн и ряда других технических и экономических факторов. Но в любом случае
частота ω0 должна быть велика по сравнению с наивысшей частотой Ωm спектра передаваемого сообщения.
Это объясняется тем, что для неискаженной передачи сообщений через радиотехнические цепи, а также для устранения искажений, возникающих при распространении радиоволн, необходимо чтобы ширина спектра сообщения Ωm была мала по сравнению с ω0; чем меньше отношение Ωm/ω0, тем меньше проявляется несовершенство характеристик системы. Поэтому чем выше требуемая скорость передачи информации и, следовательно, шире спектр сообщения Ωm, тем выше должна быть несущая частота радиосигнала. Как правило, выполняется неравенство
|
m |
/ |
1. |
|
0 |
|
Любой радиосигнал можно поэтому трактовать как «узкополосный» процесс даже при передаче «широкополосных» сообщений.
Приведем следующие примеры. При передаче речи или музыки спектр сообщения обычно ограничивают полосой от
Fmin= 30—50 Гц до Fmax = 3000—10 000 Гц. Даже на самой длинной волне вещательного диапазона λ=2000м при несущей часто-
те f0=150 к Гц отношение
F |
/ f |
0 |
max |
|
10 |
4 |
/1,5 10 |
5 |
|
|
0,06
. При
передаче тех же сообщений на коротких волнах (при частотах 15—20 МГц) это отношение не превышает сотых долей процента. При передаче подвижных изображений (телевидение) полоса частот сообщения весьма широка и достигает 5—6 МГц, однако и несущая частота выбирается не менее 50—60МГц, так что от-
ношение Fmax/f0 не превышает 10 %.
В самом общем случае радиосигнал, несущий в себе информацию, можно представить в виде
a(t) A(t) cos[ 0t (t)] A(t) cos (t), (1.17)
25

вкотором амплитуда А или фаза θ изменяются по закону передаваемого сообщения.
Если A и θ — постоянные величины, то выражение (1.17) описывает простое гармоническое колебание, не содержащее в себе никакой информации. Если A и θ (следовательно, и ψ) подвергаются принудительному изменению для передачи сообщения, то колебание становится модулированным.
Взависимости от того, какой из двух параметров изменяется — амплитуда А или угол θ — различают два основных вида модуляции: амплитудную (АМ) и угловую. Угловая модуляция,
всвою очередь, подразделяется на два вида: частотную (ЧМ) и фазовую (ФМ). Эти два вида модуляции тесно связаны между собой, и различие между ними проявляется лишь в характере изменения во времени угла ψ при одной и той же модулирующей функции.
Модулированное колебание имеет спектр, структура которого зависит как от спектра передаваемого сообщения, так и от вида модуляции. То обстоятельство, что ширина спектра модулирующего сообщения мала по сравнению с несущей часто-
той ω0, позволяет считать A (t) и ψ (t) медленными функциями времени. Это означает, что относительное изменение A (t) или θ(t) за один период несущего колебания мало по сравнению с единицей.
Рассмотрим сначала вопрос об изменении амплитуды. При скорости изменения амплитуды dA/dt приращение ампли-
туды за один период Т0 можно приближенно приравнять (dA/dt) T0, следовательно, относительное изменение за период
dA T0 |
|
dA |
|
1 |
|
2 |
. |
(1.18) |
||
|
|
|
|
|
|
|||||
dt A |
|
dt A 0 |
|
|||||||
Можно считать, что условие медленности функции A (t) выполняется, если
26

2 dA 1
0 dt A 1 или
dA 1 |
|
2 |
|
dt A |
|
|
|
|
0 |
||
|
|
|
|
.
(1.19)
Аналогично можно установить условие медленности функции θ.
Так как мгновенная частота колебания равна скорости изменения фазы то, дифференцируя аргумент выражения (1.17), находим
(t) |
d (t) |
|
d |
. |
(1.20) |
|
|
||||
|
dt |
0 |
dt |
|
|
|
|
|
|||
Производная dθ /dt определяет отклонение частоты ω(t) от частоты ω0. Это отклонение может быть быстрым или медленным. Для того чтобы колебания a (t) можно было считать близким к гармоническому, нужно, чтобы изменение частоты за время Т было мало по сравнению с частотой ω(t) в любой рассматриваемый момент времени.
Таким образом, условие медленности функции θ(t) можно записать в виде следующих неравенств:
dd
T dt dt
(t)
1
или
d |
|
(t) |
|
|
2 |
|
|
|
|
dt |
2 |
|
T |
. |
|
|
|||
|
|
|
||
(1.21)
Так как обычно ω(t) очень мало отличается от ω0, можно
считать T 2 / 0 и исходить из условия
d |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
. |
|
|
|
2 |
|||
|
|
|
|
|
|
|
dt |
2 |
|
2 |
|
0 |
|
|
|
|
|
|
||
(1.22)
Для большинства используемых в радиотехнике сигналов неравенства (1.21) обычно выполняются. Это означает, что при
27

любом виде модуляции параметры радиосигнала: амплитуда, фаза или частота — изменяются настолько медленно, что в пределах одного периода Т0 колебание можно считать гармоническим.
Эта предпосылка лежит в основе всего дальнейшего рассмотрения свойств радиосигналов и их спектров.
1.3 .Цифровая обработка аналоговых сигналов
1.3.1 Преобразование аналог—цифра. Шумы кванто-
вания
Погрешности преобразования входного сигнала из аналоговой формы в цифровую возникает при квантовании сигнала на конечное, ограниченное число уровней. Чтобы выявить характер этой погрешности приведем структурную схему (рис.1.10) и выделим из нее два устройства: аналогово-цифровой преобразователь (АЦП) и цифро-аналоговый преобразователь (ЦАП).
Рис.1.10. Функциональная схема преобразования аналогцифра и обратно – цифра-аналог
Рассмотрим сначала совместную работу этих устройств без учета цифрового фильтра при подаче на вход АЦП постоянного напряжения различного уровня u1 (рис. 1.11, а).
28
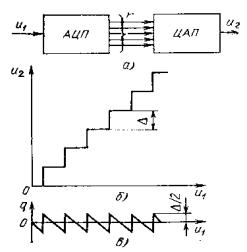
Рис. 1.11 Преобразование аналог-цифра и цифра-аналог (а), характеристика квантования (б) и ошибка квантования (в)
Основным параметром АЦП является число разрядов, используемых для кодирования входного напряжения. При двоичном коде число разрядов определяется числом триггеров регистра, каждый из которых может находиться в одном из двух состояний: с нулевым или ненулевым напряжением на выходе. Одному из этих состояний условно приписывается нуль, а другому — единица. При числе двоичных элементов r на выходе АЦП получается комбинация (кодовое число) из r символов, каждый из которых может принимать одно из двух значений (нуль или единица).
Число возможных различных комбинаций L= 2r и определяет число дискретных уровней, на которое может быть разбит диапазон изменения входного напряжения.
В ЦАП осуществляется обратное преобразование. Каждой комбинации нулей и единиц, поступающих на вход ЦАП, соответствует определенный дискретный уровень выходного напряжения. В результате при равномерном шаге квантования А
29
