Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 8

Продольные колебания стержня Лекция №8

Тема: Продольные колебания стержня.

Вопросы:

1. Постановка задачи о продольных колебаниях однородного стержня. Применение метода Фурье.

2. Вынужденные колебания стержня.

Рассмотрим задачу о продольных колебаниях однородного упругого стержня длины l, когда один его конец закреплен, а другой свободен. Эта задача сводится к интегрированию уравнения

, (6.1)

где , Е – модуль упругости материала стержня, - объемная плотность стержня, при граничных условиях

, , (6.2)

и начальных условиях

, , . (6.3)

Частные решения уравнения (6.1) найдем методом разделения переменных (методом Фурье), согласно которому

. (6.6)

Подставим это решение в исходное уравнение (6.1), получим

, ,

или, разделяя переменные,

.

Отсюда получаем два обыкновенных дифференциальных уравнения

, (6.7)

. (6.8)

Чтобы функция (6.6), отличная от тождественного нуля, удовлетворяла граничным условиям (6.2) необходимо чтобы функция Х (х) удовлетворяла граничным условиям

, (так как ). (6.9)

Поэтому для того, чтобы найти нетривиальные решения вида (6.6), удовлетворяющие граничным условиям задачи (6.2), нужно найти значения параметра , при которых существуют нетривиальные решения задачи (6.8) – (6.9), а также сами эти решения.

Интегрируя уравнение (6.8), получим

.

Используя граничные условия, получим

, .

Так как при мы получим , то положим

, , , .

Отсюда получаем , - собственные значения и соответствующие им , - собственные функции, определенные с точностью до постоянного множителя, который мы положили равным единице. При отрицательных значениях k мы получим те же собственные функции.

При уравнение (6.7) имеет решение

,

где и - произвольные постоянные. Таким образом, получим решение

==

задачи (6.1), удовлетворяющее граничным условиям (6.1) при любых и .

Составим ряд

=. (6.10)

Для определения используем начальные условия (6.2), получаем

, . (6.11)

Предположим, что ряды (6.10) и (6.11) сходятся равномерно, тогда умножая обе части первого из равенств (6.11) на и интегрируя по х на интервале , учитывая, что

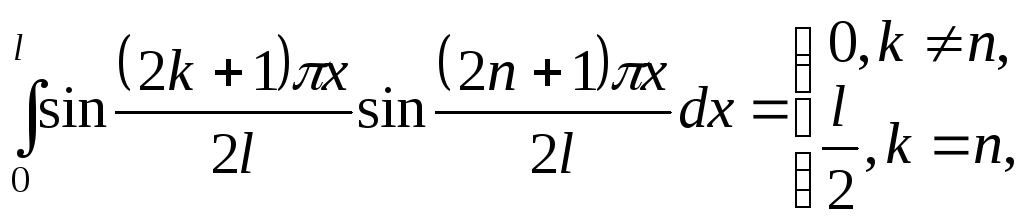
получим

.

Аналогично из второго равенства находим

.

Подставим найденные значения коэффициентов в ряд (6.10), получим решение задачи (6.1) – (6.3), если ряд (6.10) и ряды, полученные из него двукратным почленным дифференцированием по х и t, равномерно сходятся.

Пример 6.1. Стержень подвешен вертикально и защемлен так, что смещение во всех точках равно нулю. В момент времени стержень освобождается, оставаясь закрепленным в верхней точке. Изучить вынужденные колебания стержня.

Решение. Составим дифференциальное уравнение, соответствующее условию задачи. Так как колебания стержня происходят под действием силы тяжести, то данная задача сводится к решению уравнения:

,

где g – ускорение силы тяжести.

Так как один конец закреплен, а другой конец свободен и в начальный момент смещение во всех точках равно нулю, то получаем следующие граничные условия:

,

и начальные условия

, .

Решение поставленной задачи будем искать в виде сумы

решения неоднородного уравнения v, удовлетворяющего только однородным граничным условиям и решения однородного уравнения w, удовлетворяющего однородным граничным условиям и начальным условиям:

,

,

т.е. необходимо решить задачи:

, (6.12)

, (6.13)

и

,

,

, .

Решение задачи (6.12), (6.13) будем искать в виде функции дважды непрерывно дифференцируемой по х:

,

тогда уравнение (6.12) примет вид

,

т.е. ,

следовательно, .

Используя граничные условия, получим

, ,

следовательно,

, .

Таким образом, решением задачи (6.12), (6.13) будет функция

,

.

Решим вторую задачу, которая принимает вид:

,

,

, .

Эта задача решается методом разделения переменных. Решение будем искать в виде

,

Подставим это решение в исходное уравнение, получим

, ,

или, разделяя переменные,

.

Это равенство возможно только в том случае, когда его обе части не зависят ни от х, ни от t, т.е. равны одной и той же постоянной, обозначим ее через , тогда

.

Получаем два обыкновенных дифференциальных уравнения

,

. (6.14)

Воспользуемся теперь граничными условиями, откуда

, ,

и так как , то функция Х (х) должна удовлетворять граничным условиям

, .

Поэтому нужно найти нетривиальные решения уравнения

,

удовлетворяющие граничным условиям

, .

1. , тогда общее решение уравнения (6.14) имеет вид

.

Используя граничные условия, будем иметь

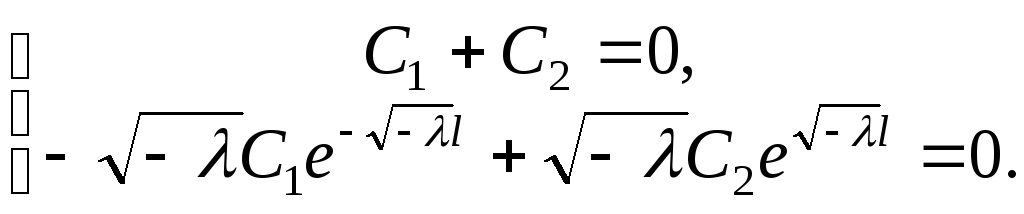
Так как определитель , то и, следовательно, , т.е. в этом случае нетривиальных решений нет.

2. , , , . Отсюда и .

3. При корни характеристического уравнения и .

Используя граничные условия, получим

,

, или .

Так как при мы опять получим , то положим

, , .

Отсюда получаем 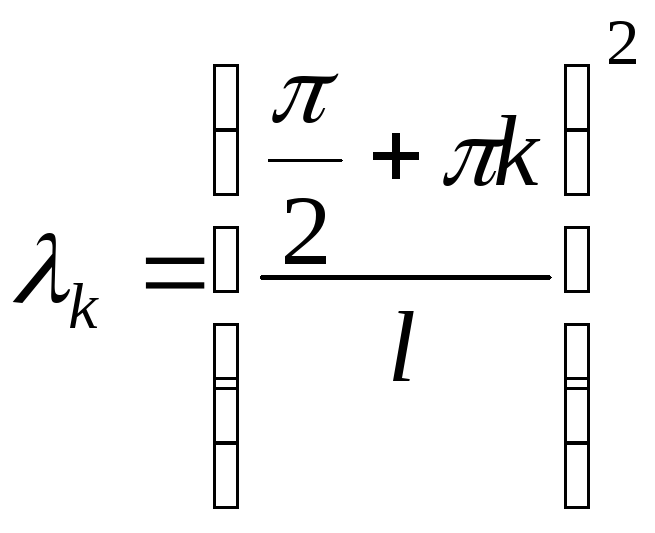, - собственные значения и соответствующие им 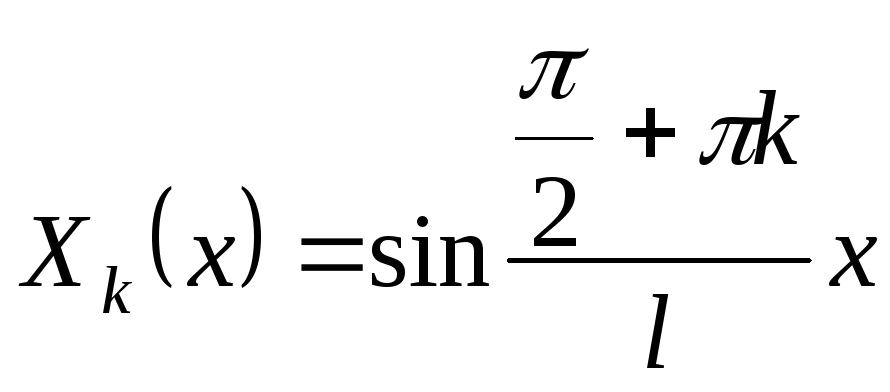- собственные функции.

При уравнение

имеет решение

.

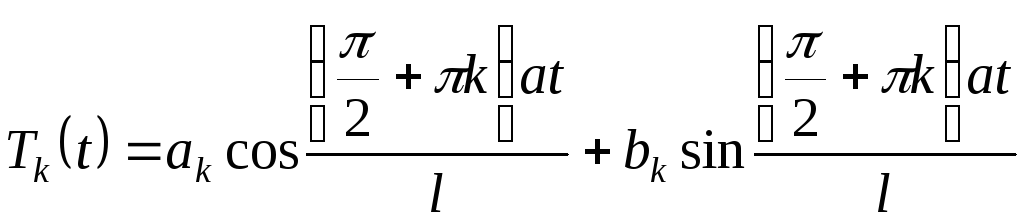Используя и , получим решение

==,

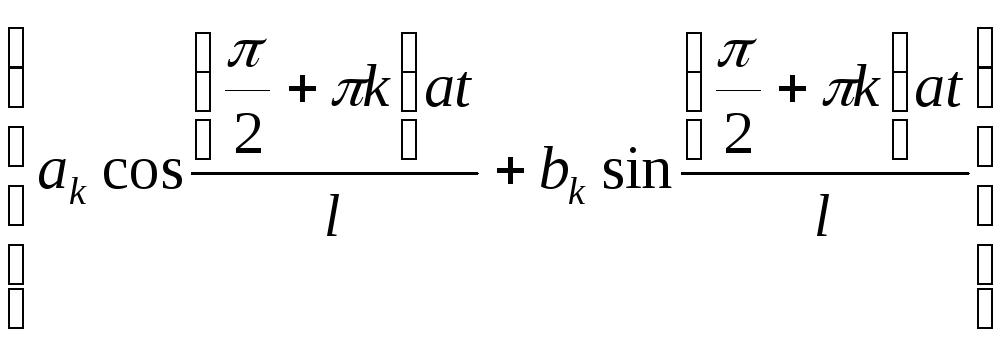
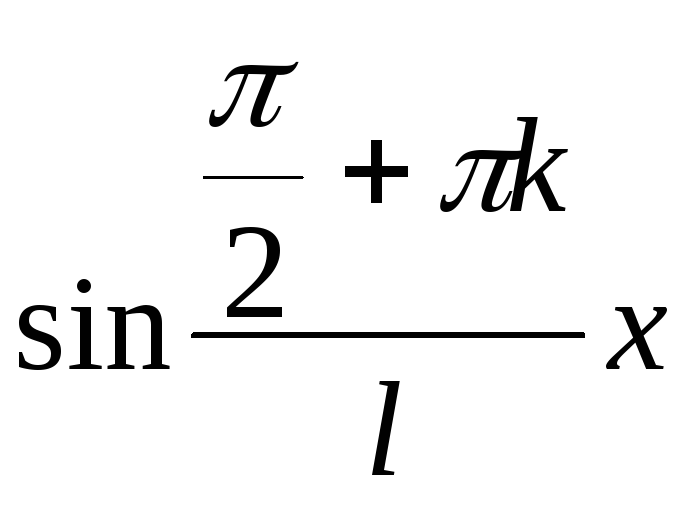удовлетворяющее граничным условиям.

=

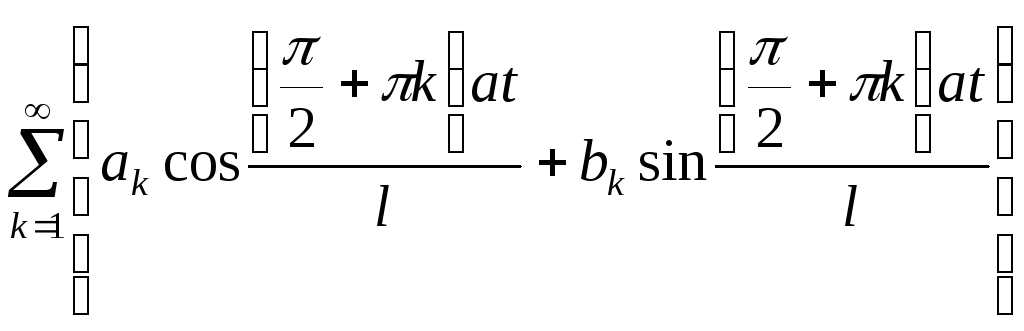
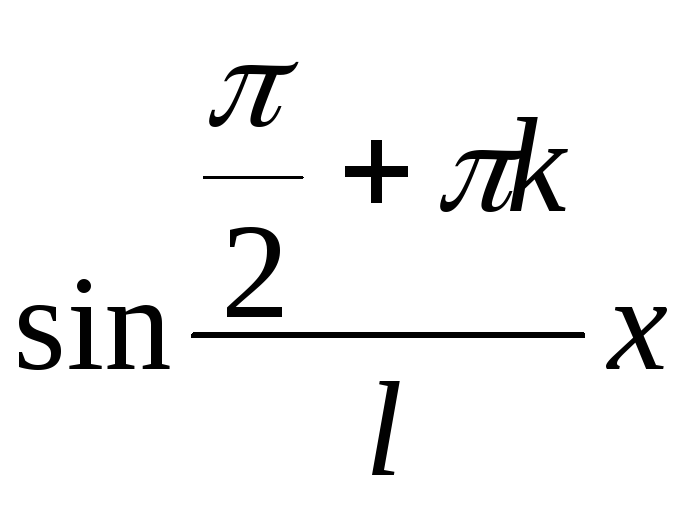
Для определения получаем

,

.

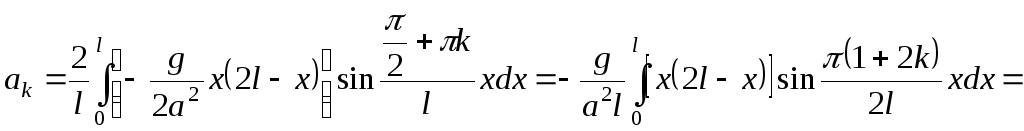
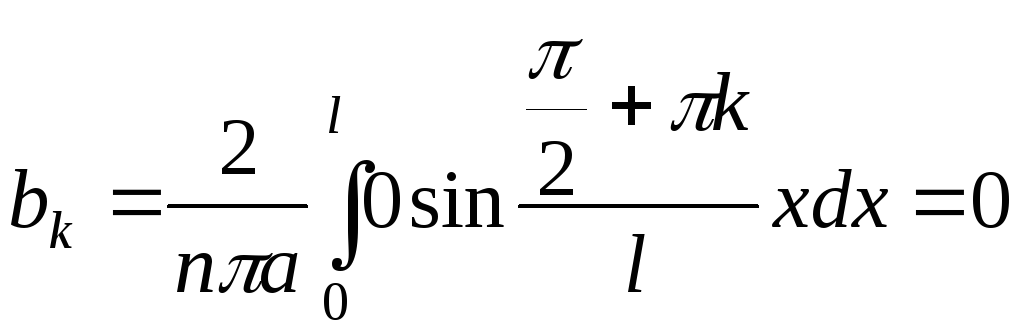Поэтому, имеем

=.

Окончательно, получаем

.

40